Слайд 2Повторение изученного материала

Слайд 3Дайте определение сложной электрической цепи
Сложными называются разветвленные электрические цепи со многими источниками

энергии.
Слайд 4Дайте формулировку I закону Кирхгофа
Алгебраическая сумма токов в каждом узле любой цепи

равна нулю. При этом направленный к узлу ток принято считать положительным, а направленный от узла — отрицательным.
Слайд 5Дайте формулировку II закону Кирхгофа
Алгебраическая сумма падений напряжений на всех ветвях,

принадлежащих любому замкнутому контуру цепи, равна алгебраической сумме ЭДС ветвей этого контура.
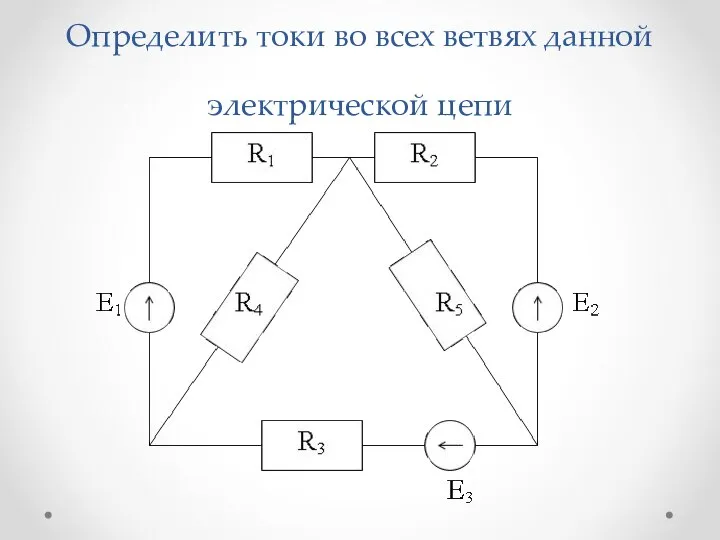
Слайд 7Определить токи во всех ветвях данной электрической цепи
Слайд 8Найдем общее количество уравнений
Для определения токов во всех ветвях данной электрической цепи,

необходимо составить систему уравнений по законам Кирхгофа.
Общее число уравнений в системе должно соответствовать числу неизвестных токов, т. е. числу ветвей.
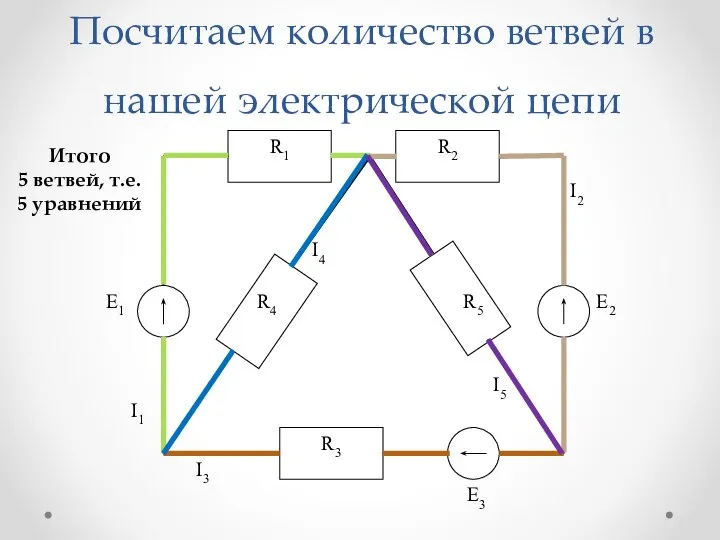
Слайд 9Посчитаем количество ветвей в нашей электрической цепи
Итого
5 ветвей, т.е.
5 уравнений
Слайд 10Найдем количество уравнений по I закону Кирхгофа
По первому закону Кирхгофа составляется число

уравнений, на единицу меньшее числа узлов цепи, т.к. уравнение для последнего узла есть следствие всех предыдущих уравнений и не дает ничего нового для расчета.
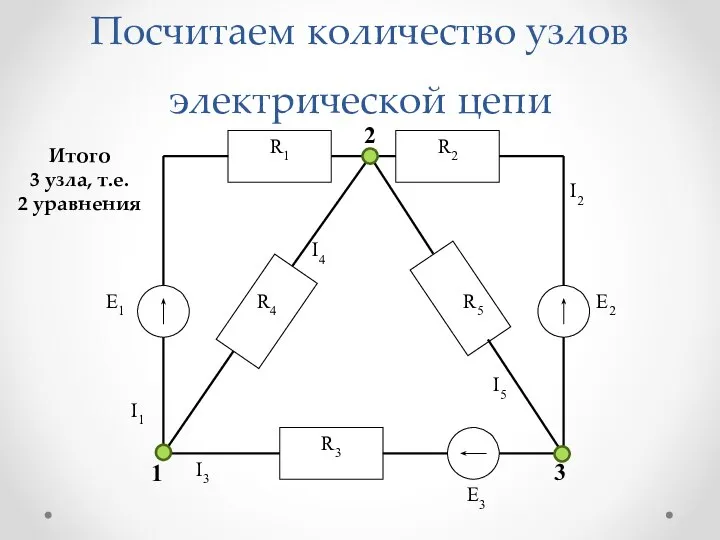
Слайд 11Посчитаем количество узлов электрической цепи
1
2
3
Итого
3 узла, т.е.
2 уравнения
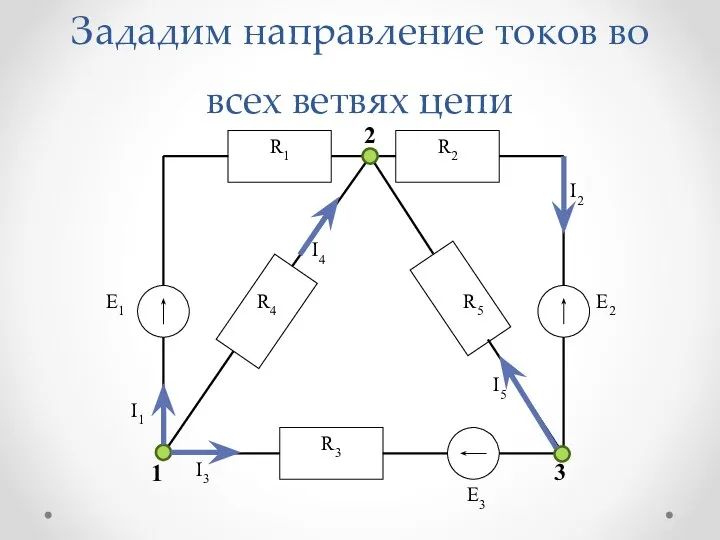
Слайд 12Зададим направление токов во всех ветвях цепи
1
2
3
Слайд 13Составим уравнения по I закону Кирхгофа
Токи, подходящие к узлу, будем считать положительными

и брать со знаком (+), а токи, отходящие от узла – (–).
Слайд 141
2
3
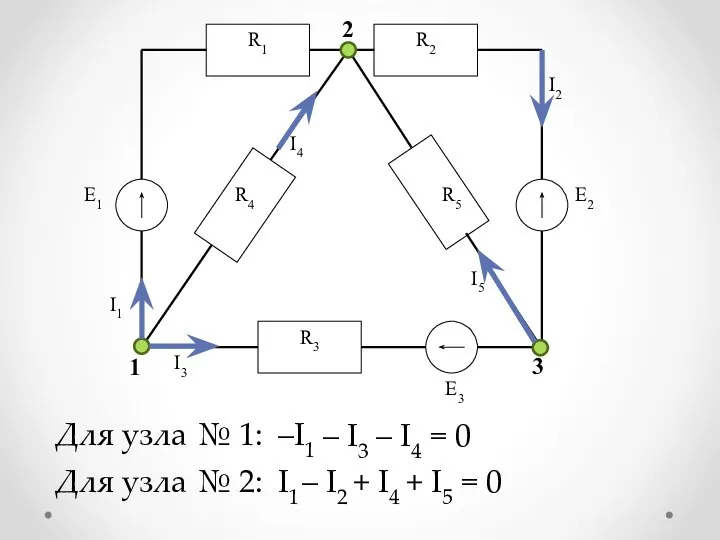
Для узла № 1:
–I1
– I3
– I4
= 0
Для узла № 2:
I1
+
Слайд 15Найдем количество уравнений по II закону Кирхгофа
По второму закону Кирхгофа составляются все

недостающие уравнения для любых произвольно выбранных контуров цепи.
Посчитаем количество недостающих уравнений: 5 – 2 = 3.
Слайд 16Зададим направление обхода выбранных контуров
1
2
3
I
II
III
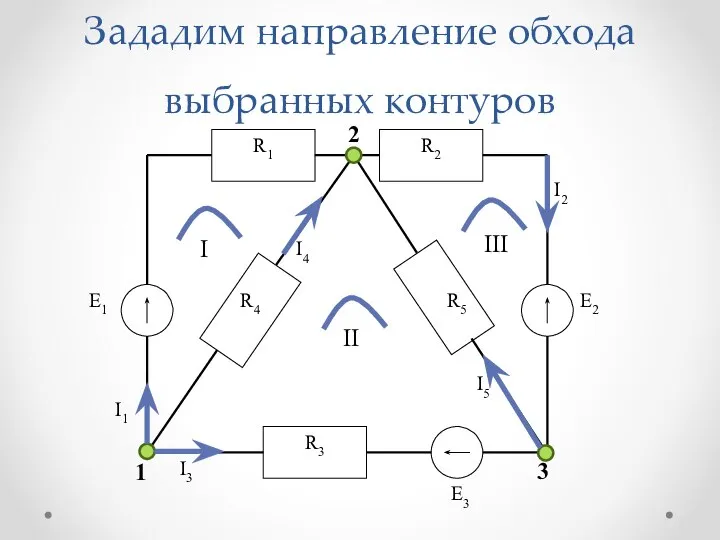
Слайд 17Составим уравнения по II закону Кирхгофа
При составлении уравнений ЭДС и токи, совпадающие

с выбранным направлением обхода контура будем брать со знаком (+), а несовпадающие – со знаком (–).
Слайд 181
2
3
I
II
III
Для I контура:
I1R1
= Е1
– I4R4
Для II контура:
I4R4
= Е3
– I5R5
Для III
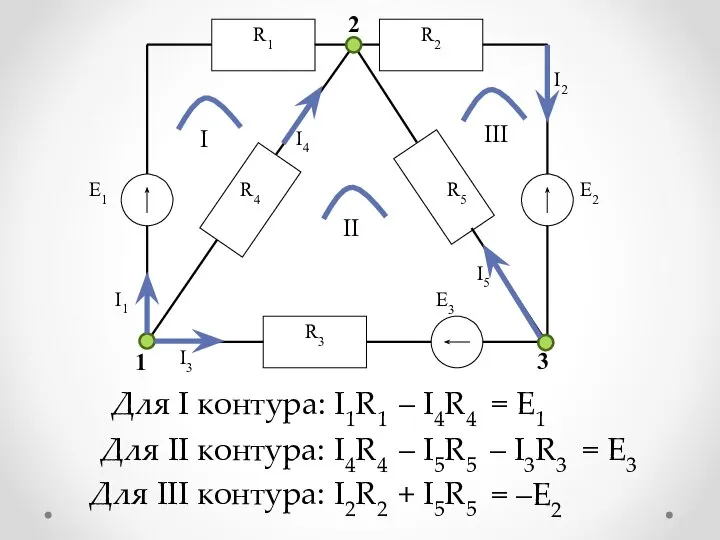
контура:
I2R2
= –Е2
+ I5R5
– I3R3
Слайд 19Получилась система уравнений
–I1 – I3 – I4 = 0
I1 – I2 +

I4 + I5 = 0
I1R1 – I4R4 = E1
I4R4 – I5R5 – I3R3 = E3
I2R2 + I4R4 = –E2
Решив ее, получаем пять значений токов.


















 Закон Ома для участка цепи
Закон Ома для участка цепи Кинематика 3. Движение тела, брошенного горизонтально или под углом к горизонту
Кинематика 3. Движение тела, брошенного горизонтально или под углом к горизонту Урок 21+ Розв'язування задач
Урок 21+ Розв'язування задач Расчёт количества теплоты при плавлении и кристаллизации тел
Расчёт количества теплоты при плавлении и кристаллизации тел Переменный электрический ток
Переменный электрический ток Смачивание. Капиллярнность
Смачивание. Капиллярнность Закон сохранения полной механической энергии
Закон сохранения полной механической энергии Лампа накаливания
Лампа накаливания Домашнее задание по физике
Домашнее задание по физике Три состояния вещества. Различие в молекулярном строении твердых тел, жидкостей и газов
Три состояния вещества. Различие в молекулярном строении твердых тел, жидкостей и газов Полный цикл изготовления телескопов в домашних условиях
Полный цикл изготовления телескопов в домашних условиях Проводники в электростатическом поле
Проводники в электростатическом поле Да здравствует российская наука
Да здравствует российская наука Магнитореологический амортизатор
Магнитореологический амортизатор Анализ миссии Корпоративной Академии Росатома
Анализ миссии Корпоративной Академии Росатома Модели атомов. Опыт Резерфорда
Модели атомов. Опыт Резерфорда Измерительная система определения теплофизических свойств твердых и сыпучих материалов на базе прибора ИТ – 3
Измерительная система определения теплофизических свойств твердых и сыпучих материалов на базе прибора ИТ – 3 Трехфазные цепи
Трехфазные цепи Расчет свободной энергии с помощью молекулярной динамики
Расчет свободной энергии с помощью молекулярной динамики Презентация на тему Плавление и кристаллизация
Презентация на тему Плавление и кристаллизация  Количество вщства. Решение задач
Количество вщства. Решение задач Интерференция света. Электромагнитная природа света
Интерференция света. Электромагнитная природа света Методические указания к выполнению отчета по лабораторным работам
Методические указания к выполнению отчета по лабораторным работам Интерференция и дифракция света
Интерференция и дифракция света Техническая механика. Термины и определения
Техническая механика. Термины и определения Колыбель Ньютона
Колыбель Ньютона Теплотехника. Основные определения и понятия. Параметры состояния. Уравнения состояния
Теплотехника. Основные определения и понятия. Параметры состояния. Уравнения состояния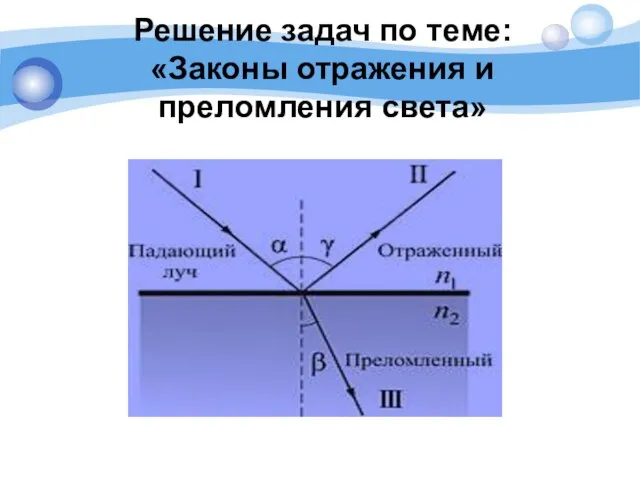 Решение задач по теме: Законы отражения и преломления света
Решение задач по теме: Законы отражения и преломления света