Дифракция света

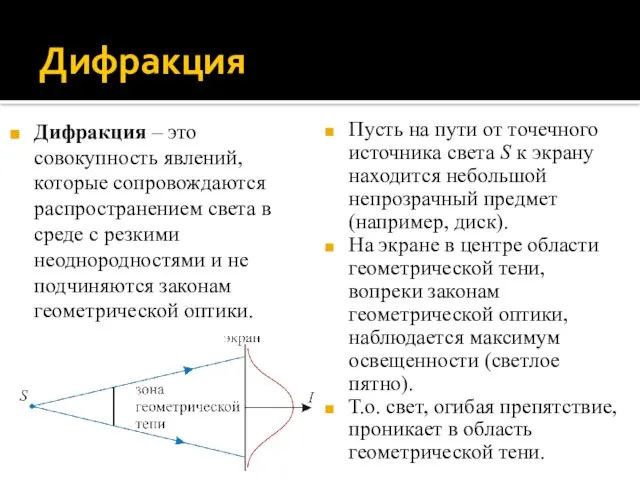
Дифракция
Дифракция – это совокупность явлений, которые сопровождаются распространением света в среде с резкими неоднородностями и не подчиняются законам геометрической оптики.
Пусть на пути от точечного источника света S к экрану находится небольшой непрозрачный предмет (например, диск).
На экране в центре области геометрической тени, вопреки законам геометрической оптики, наблюдается максимум освещенности (светлое пятно).
Т.о. свет, огибая препятствие, проникает в область геометрической тени.

Необходимое условие наблюдения дифракции света
Для наблюдения дифракционных явлений необходимо, чтобы длина световой волны λ была сравнима по величине с характерным размером b препятствий (неоднородностей среды).

Интерференция и дифракция
Физическая сущность явлений интерференции и дифракции одинакова и заключается в пространственном перераспределении интенсивности света в результате наложения когерентных волн.
При этом интерференция возникает при наложении волн от двух или нескольких дискретно расположенных в пространстве точечных источников света.
Дифракционные явления – это результат наложения световых волн от бесконечного множества эффективных точечных источников, распределенных в пространстве непрерывно.

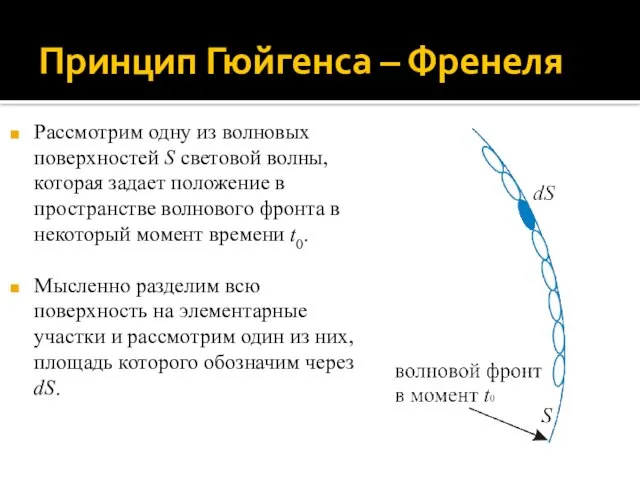
Принцип Гюйгенса – Френеля
Рассмотрим одну из волновых поверхностей S световой волны, которая задает положение в пространстве волнового фронта в некоторый момент времени t0.
Мысленно разделим всю поверхность на элементарные участки и рассмотрим один из них, площадь которого обозначим через dS.

Интерференция и дифракция
Принцип Гюйгенса – Френеля: каждый элементарный участок dS волновой поверхности распространяющейся в пространстве световой волны можно рассматривать в качестве точечного источника вторичной волны (в однородной и изотропной среде – сферической волны). В любой точке пространства, которую волна достигает позднее, колебание электромагнитного поля представляет собой суперпозицию колебаний, порожденных вторичными волнами всех элементов волновой поверхности S. В частности, в любой момент времени t > t0 волновой фронт можно получить, построив огибающую волновых фронтов вторичных волн.

Принцип Гюйгенса – Френеля
В соответствии с принципом Гюйгенса – Френеля, каждый участок dS волновой поверхности излучает вторичную волну, световой вектор dE которой в каждой точке P пространства, расположенной на расстоянии r от элемента dS, может быть представлен в виде:
Здесь (ωt + α) фаза колебания в месте расположения участка dS,
k – волновое число, числовой множитель A зависит от амплитуды световой волны в месте, где расположен элемент dS.

Принцип Гюйгенса – Френеля
Коэффициент K зависит от угла ϕ между нормалью n к dS и направлением от dS в точку P: значению ϕ = 0 соответствует K = 1, значению ϕ = π/2 – значение K = 0.
Световой вектор результирующего колебания в точке P:
Этот интеграл называется интегралом Френеля

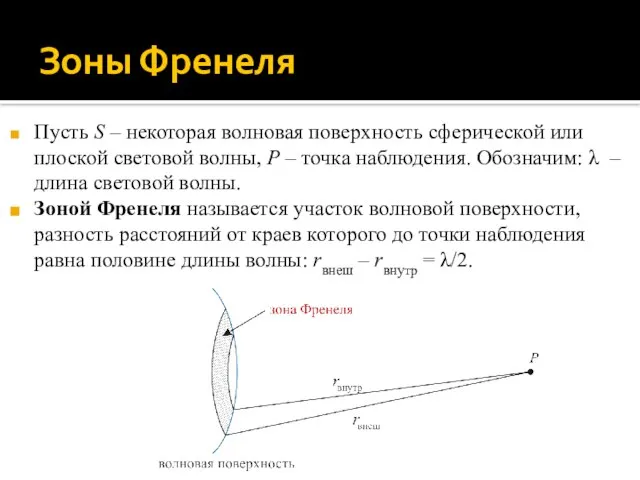
Зоны Френеля
Пусть S – некоторая волновая поверхность сферической или плоской световой волны, P – точка наблюдения. Обозначим: λ – длина световой волны.
Зоной Френеля называется участок волновой поверхности, разность расстояний от краев которого до точки наблюдения равна половине длины волны: rвнеш – rвнутр = λ/2.

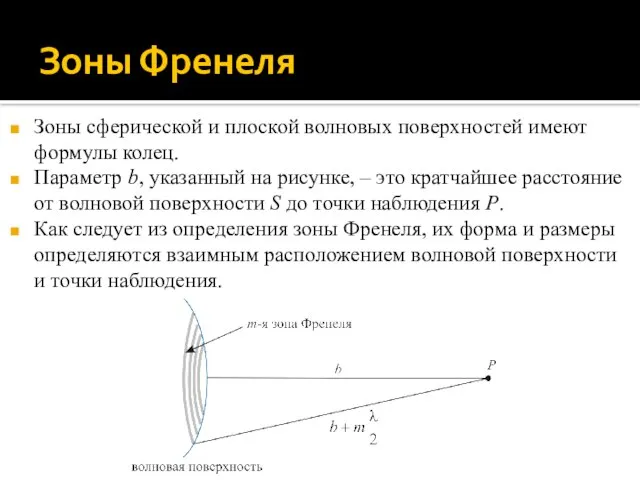
Зоны Френеля
Зоны сферической и плоской волновых поверхностей имеют формулы колец.
Параметр b, указанный на рисунке, – это кратчайшее расстояние от волновой поверхности S до точки наблюдения P.
Как следует из определения зоны Френеля, их форма и размеры определяются взаимным расположением волновой поверхности и точки наблюдения.

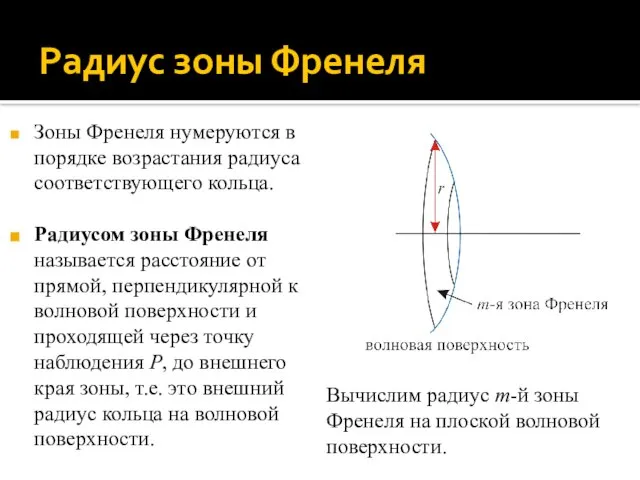
Радиус зоны Френеля
Зоны Френеля нумеруются в порядке возрастания радиуса соответствующего кольца.
Радиусом зоны Френеля называется расстояние от прямой, перпендикулярной к волновой поверхности и проходящей через точку наблюдения P, до внешнего края зоны, т.е. это внешний радиус кольца на волновой поверхности.
Вычислим радиус m-й зоны Френеля на плоской волновой поверхности.

Радиус зоны Френеля
В соответствии с определением, расстояние rвнеш от внешнего края m-й зоны до точки наблюдения P равно:
Таким образом, имеем:
Здесь мы учли, что расстояние b намного больше длины световой волны λ

Радиус зоны Френеля
Можно показать, что для сферической световой волны радиус rm m-й зоны Френеля:
Здесь a – расстояние от источника сферической волны до волновой поверхности S, b – расстояние от волновой поверхности S до точки наблюдения P

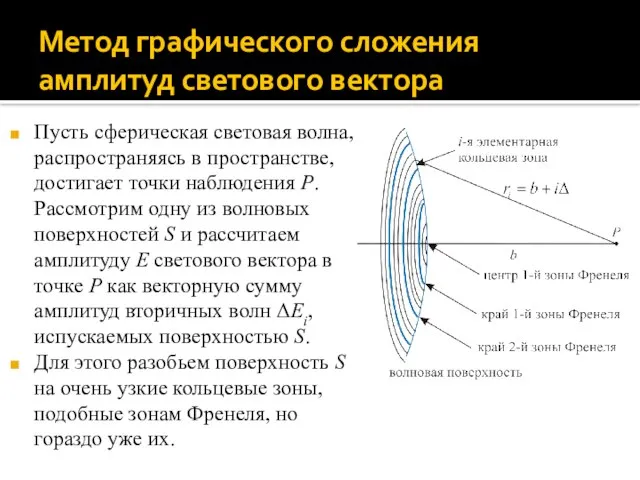
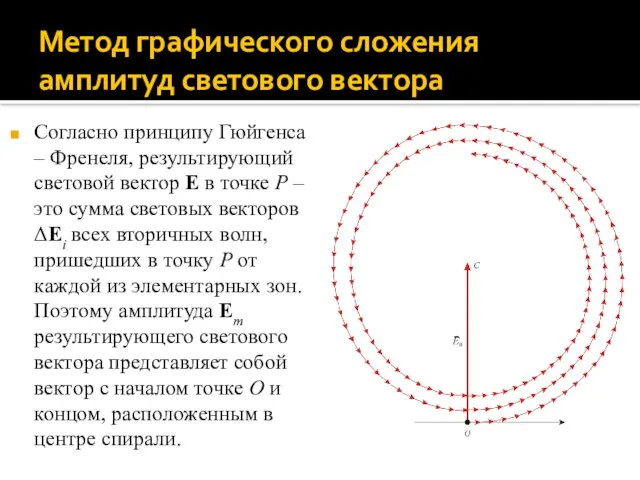
Метод графического сложения амплитуд светового вектора
Пусть сферическая световая волна, распространяясь в пространстве, достигает точки наблюдения P. Рассмотрим одну из волновых поверхностей S и рассчитаем амплитуду E светового вектора в точке P как векторную сумму амплитуд вторичных волн ΔEi, испускаемых поверхностью S.
Для этого разобьем поверхность S на очень узкие кольцевые зоны, подобные зонам Френеля, но гораздо уже их.

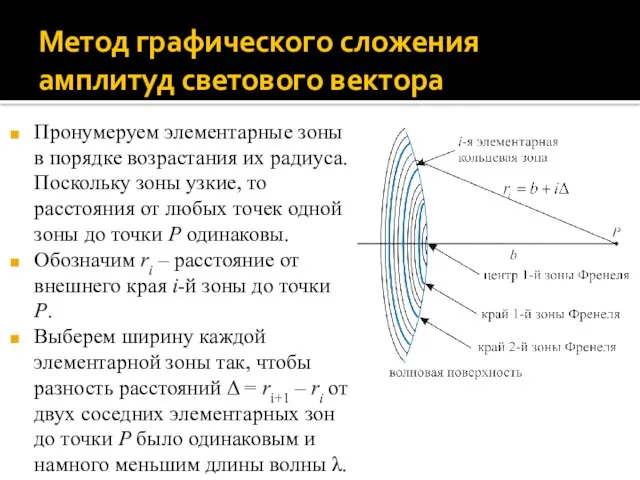
Метод графического сложения амплитуд светового вектора
Пронумеруем элементарные зоны в порядке возрастания их радиуса. Поскольку зоны узкие, то расстояния от любых точек одной зоны до точки P одинаковы.
Обозначим ri – расстояние от внешнего края i-й зоны до точки P.
Выберем ширину каждой элементарной зоны так, чтобы разность расстояний Δ = ri+1 – ri от двух соседних элементарных зон до точки P было одинаковым и намного меньшим длины волны λ.

Метод графического сложения амплитуд светового вектора
Если кратчайшее расстояние от волновой поверхности до точки P равно b, то ri = b + iΔ.
Тогда световой вектор волны, пришедшей в точку P от участка i-й элементарной зоны:
Здесь δ - разность фаз двух вторичных волн, пришедших в точку P от двух соседних зон.

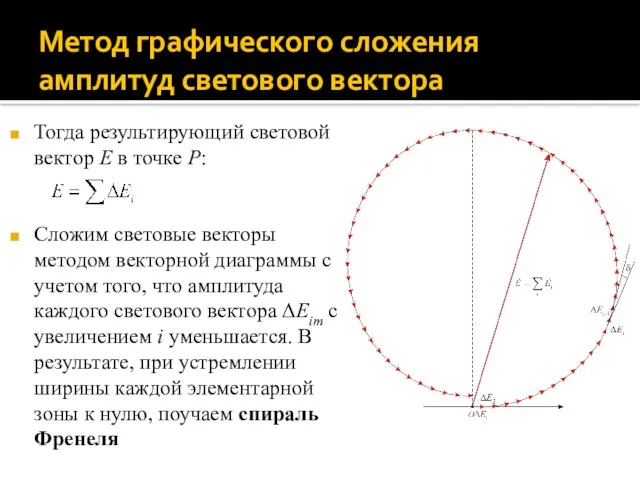
Метод графического сложения амплитуд светового вектора
Тогда результирующий световой вектор E в точке P:
Сложим световые векторы методом векторной диаграммы с учетом того, что амплитуда каждого светового вектора ΔEim с увеличением i уменьшается. В результате, при устремлении ширины каждой элементарной зоны к нулю, поучаем спираль Френеля

Метод графического сложения амплитуд светового вектора
Согласно принципу Гюйгенса – Френеля, результирующий световой вектор E в точке P – это сумма световых векторов ΔEi всех вторичных волн, пришедших в точку P от каждой из элементарных зон. Поэтому амплитуда Em результирующего светового вектора представляет собой вектор с началом точке O и концом, расположенным в центре спирали.

Метод графического сложения амплитуд светового вектора
Построим на векторной диаграмме световые векторы, соответствующие колебаниям от:
центра 1-й зоны Френеля;
края 1-й зоны Френеля
края 2-й зоны Френеля

6.2 Дифракция Френеля на круглом отверстии и диске
ЛЕКЦИЯ 6. ДИФРАКЦИЯ СВЕТА

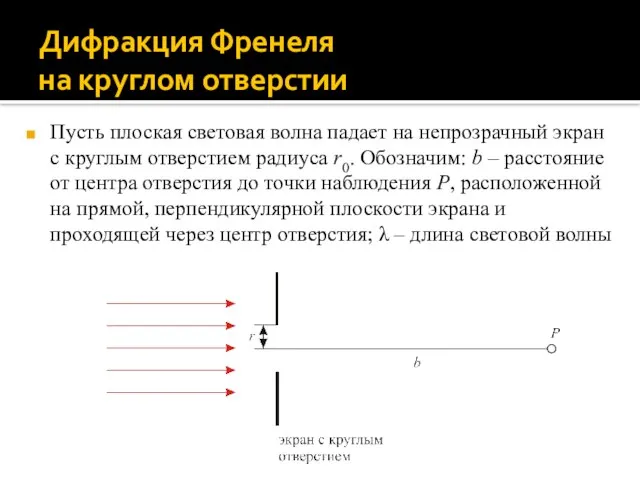
Дифракция Френеля
на круглом отверстии
Пусть плоская световая волна падает на непрозрачный экран с круглым отверстием радиуса r0. Обозначим: b – расстояние от центра отверстия до точки наблюдения P, расположенной на прямой, перпендикулярной плоскости экрана и проходящей через центр отверстия; λ – длина световой волны

Дифракция Френеля
на круглом отверстии
Определим интенсивность света в точке наблюдения P. С этой целью найдем число зон Френеля, которые благодаря отверстию остаются открытыми на волновой поверхности падающей волны, если наблюдать за ней из точки P. Приравняем радиус отверстия r0 к радиусу rm m-й зоны Френеля:
Здесь m – число открытых отверстием зон Френеля, (может быть целым или нецелым числом)

Дифракция Френеля
на круглом отверстии
Значение m (число открытых отверстием зон Френеля) зависит от параметра b, т.е. от веста расположения точки наблюдения относительно экрана с отверстием. Если радиус отверстия r0 остается неизменным, то при изменении положения точки наблюдения P число открытых зон меняется.

Дифракция Френеля
на круглом отверстии
Интенсивность света в точке P приближенно можно определить с помощью метода векторной диаграммы колебаний светового вектора.
Пусть m = 1 (отверстие открывает только первую зону Френеля). Тогда (см. рисунок) амплитуда светового вектора E = 2E0. Таким образом, I ~ E02 = 4I0.
Если m = 2 (отверстие открывает первую и вторую зоны Френеля), то, как видно из рисунка, E ≈ 0 и I ≈ 0.

Амплитудная зонная пластинка
Таким образом, для небольших значений m справедливо следующее утверждение: интенсивность в точке наблюдения зависит от того, четное или нечетное число зон Френеля открыто отверстием: если число нечетное, то в точке наблюдения образуется светлое пятно, если четное – темное.
Значительно большее усиление света в точке P можно осуществить, если изготовить стеклянную пластинку, на поверхность которой нанесено непрозрачное покрытие в виде колец, закрывающих только четные (или только нечетные) зоны Френеля. Такая пластинка называется амплитудной зонной пластинкой.

Фазовая зонная пластинка
Еще большего эффекта усиления света можно достичь, не перекрывая четные/нечетные зоны Френеля, а изменяя фазу колебаний на π.
Это можно осуществить с помощью прозрачной пластинки, толщина которой в местах, соответствующих четным и нечетным зонам, отличается ровно на такую величину, что соответствующая этой величине длина пути составляет λ/2.
Таким образом, если абсолютный показатель преломления стекла равен n, то толщина стекла в области четных и нечетных зон Френеля должна отличаться на величину h, удовлетворяющую условию nh = λ/2. Тогда вторичные волны будут приходить в точку P не в противофазе, а в фазе.
Такая пластинка называется фазовой зонной пластинкой.

Дифракция Френеля
на круглом диске
Если на пути световой волны поместить непрозрачный диск, то в любой точке наблюдения P на прямой, перпендикулярной плоскости диска и проходящей через его центр, т.е. в области геометрической тени, интенсивность света будет отлична от нуля.

Дифракция Френеля
на круглом диске
Пусть, например, радиус диска равен радиусу первой зоны Френеля. Тогда на векторной диаграмме колебаний вектора E в точке P отсутствует участок, соответствующий первой зоне Френеля. Тогда, как видно из рисунка, E = E0 и I = I0.
Во всех случаях, когда диск закрывает m зон Френеля, на векторной диаграмме отсутствуют m полувитков спирали. И если m не слишком велико, то E = E0 и I = I0. Т.е. интенсивность света в точке P почти не отличается от интенсивности падающей волны.

6.3 Дифракция Фраунгофера на прямоугольной щели
ЛЕКЦИЯ 6. ДИФРАКЦИЯ СВЕТА

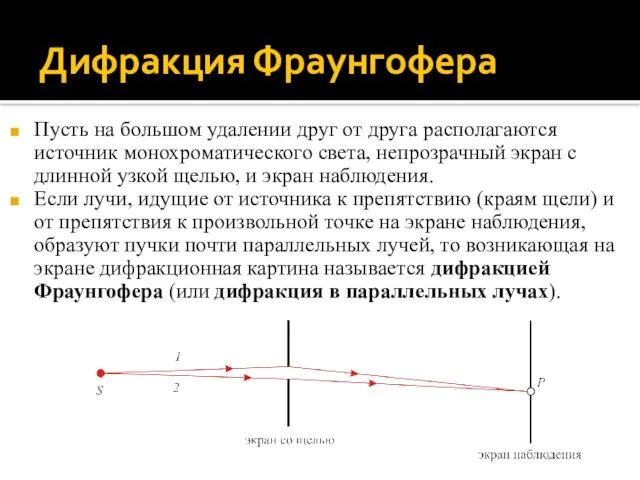
Дифракция Фраунгофера
Пусть на большом удалении друг от друга располагаются источник монохроматического света, непрозрачный экран с длинной узкой щелью, и экран наблюдения.
Если лучи, идущие от источника к препятствию (краям щели) и от препятствия к произвольной точке на экране наблюдения, образуют пучки почти параллельных лучей, то возникающая на экране дифракционная картина называется дифракцией Фраунгофера (или дифракция в параллельных лучах).

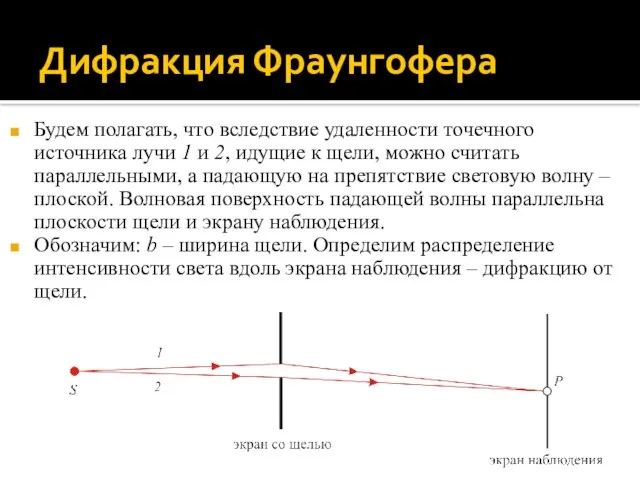
Дифракция Фраунгофера
Будем полагать, что вследствие удаленности точечного источника лучи 1 и 2, идущие к щели, можно считать параллельными, а падающую на препятствие световую волну – плоской. Волновая поверхность падающей волны параллельна плоскости щели и экрану наблюдения.
Обозначим: b – ширина щели. Определим распределение интенсивности света вдоль экрана наблюдения – дифракцию от щели.

Дифракция Фраунгофера от щели
Положение точки наблюдения P на кране задается углом ϕ между нормалью к плоскости щели и направлением QP от середины щели к точке P; за положительное направление отсчета угла ϕ примем поворот отрезка QP по часовой стрелке.
Направим ось Y перпендикулярно щели, начало оси совместим с серединой щели – точкой Q. Координаты краев щели: –b/2 и +b/2.

Дифракция Фраунгофера от щели
Мысленно разделим поверхность щели на элементарные полосы толщиной dy, края которых параллельны краям щели.
Обозначим: r0 – длина отрезка QP, тогда в силу параллельности всех лучей,
Все вторичные волны от одной элементарной полосы приходят в точку P в одинаковой фазе, т.е.:
Здесь Ady – амплитуда колебания, пропорциональная площади участка излучения (ширине dy элементарной полосы).

Дифракция Фраунгофера от щели
Результирующее колебание светового вектора E в точке наблюдения P представляет собой сумму колебаний, порожденных всеми элементарными полосами, на которые мысленно разбита щель:
Интенсивность волны:
Здесь I0 – интенсивность света в точке наблюдения, расположенной напротив середины щели (ϕ = 0)

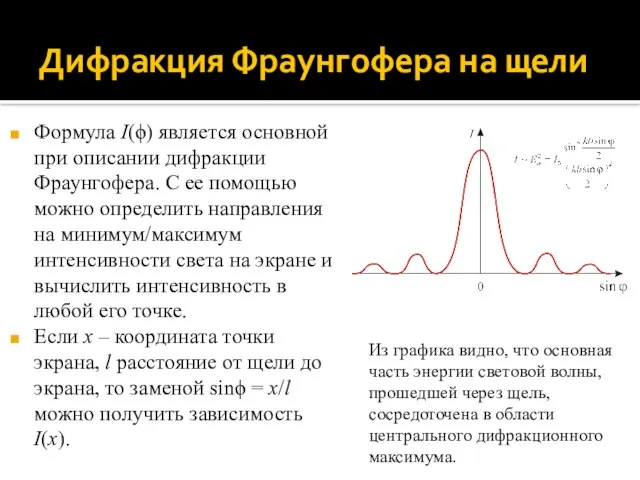
Дифракция Фраунгофера на щели
Формула I(ϕ) является основной при описании дифракции Фраунгофера. С ее помощью можно определить направления на минимум/максимум интенсивности света на экране и вычислить интенсивность в любой его точке.
Если x – координата точки экрана, l расстояние от щели до экрана, то заменой sinϕ = x/l можно получить зависимость I(x).
Из графика видно, что основная часть энергии световой волны, прошедшей через щель, сосредоточена в области центрального дифракционного максимума.

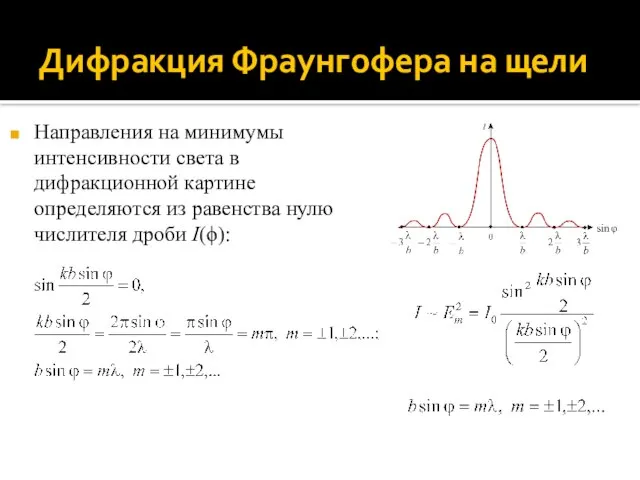
Дифракция Фраунгофера на щели
Направления на минимумы интенсивности света в дифракционной картине определяются из равенства нулю числителя дроби I(ϕ):

Дифракция Фраунгофера на щели
Направления на первые (m = ±1) минимумы дифракции:
Угол ϕ1 называется угловой полушириной дифракционного максимума. Для малых углов угловая полуширина дифракционного максимума
Всякий пучок лучей с характерным поперечным размером b (например, ширина щели, диаметр диафрагмы) характеризуется дифракционном уширением, равным по порядку величины угловой полуширине δϕ центрального дифракционного максимума.

6.4 Многолучевая интерференция
ЛЕКЦИЯ 6. ДИФРАКЦИЯ СВЕТА

Многолучевая интерференция
Рассмотрим интерференцию волн, излучаемых несколькими точечными когерентными источниками света – многолучевую интерференцию.
Пусть в однородной изотропной среде с ε = μ = 1 имеется N расположенных вдоль одной прямой когерентных источников света, колебания которых происходят в одинаковой фазе ωt, где ω – циклическая частота. Расстояние между соседними источниками равно d. Определим интенсивность излучения в точке наблюдения P.

Многолучевая интерференция
Поскольку точка P находится на большом удалении от источников, то лучи, идущие от источников в точку P можно считать параллельными друг другу. Будем также предполагать, что амплитуды волн от всех источников одинаковы.
Обозначим θ – угол между нормалью к линии, вдоль которой расположены источники и направлением на точку P.
Расстояние от i-го источника до точки P равно:
ri = r1 +(i – 1)dsinθ, где dsinθ – оптическая разность хода лучей, идущих от двух соседних источников.

Многолучевая интерференция
Каждый источник с порядковым номером i порождает в точке P колебание светового вектора Ei:
Здесь Em – амплитуда колебания, возбужденного в точке P волной от одного источника и одинаковая для всех источников.

Многолучевая интерференция
Результирующее колебание E светового вектора в точке P равно сумме всех колебаний:
Для вычисления E воспользуемся методом векторной диаграммы.
Все складываемые колебания имеют одинаковую амплитуду Em, разность фаз между колебания от двух соседних источников равна δ = kdsinθ, поэтому вектор каждого колебания имеет длину Em и повернут на угол δ против часовой стрелки по отношению к вектору предыдущего колебания.
Векторная диаграмма представлена на следующем слайде.

Многолучевая интерференция
Векторная диаграмма представляет собой часть правильного N-угольника, со стороной Em. Результирующее колебание изображается на диаграмме вектором E. Из простых геометрических соображений ясно, что его длина:

Зависимость интенсивности света от угла дифракции
Тогда интенсивность I света в точке P, пропорциональная квадрату амплитуды Em светового вектора, равна
Здесь I0 – интенсивность световой волны, пришедшей в точку P от каждого из N источников, пропорциональная квадрату амплитуды Em.
Таким образом, интенсивность света в точке наблюдения P зависит от угла θ, определяющего направление наблюдения.

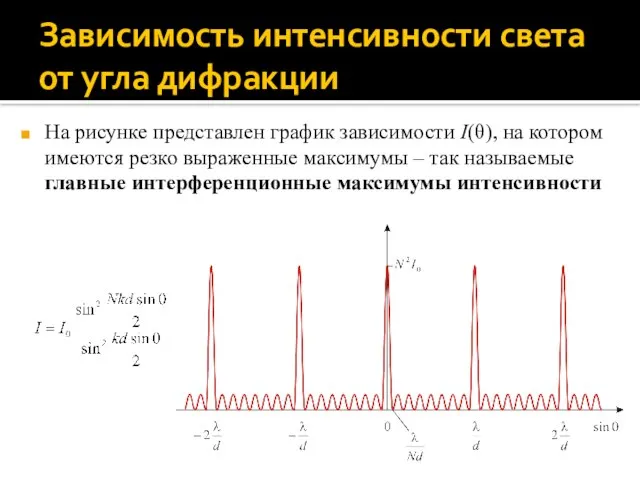
Зависимость интенсивности света от угла дифракции
На рисунке представлен график зависимости I(θ), на котором имеются резко выраженные максимумы – так называемые главные интерференционные максимумы интенсивности

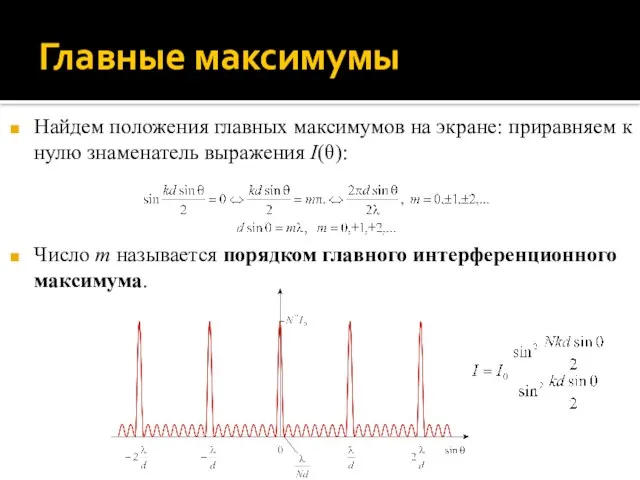
Главные максимумы
Найдем положения главных максимумов на экране: приравняем к нулю знаменатель выражения I(θ):
Число m называется порядком главного интерференционного максимума.

Главные максимумы
Таким образом, углы, определяющие направления на главные максимумы интенсивности в интерференционной картине от N когерентных источников света, должны удовлетворять условию:

Интенсивность главного максимума
Теперь найдем значение интенсивности света в центральном (m = 0) главном максимуме, для которого θ = 0 и тогда значение разности фаз складываемых колебаний δ = kdsinθ = 0.
Тогда, согласно выражению для I(θ):
Т.о. интенсивность света в главном максимуме в N2 раз превышает интенсивность света I0 от отдельного взятого источника.

Интенсивность главного максимума
Оценим угловую ширину δθ центрального максимума, т.е. угловое расстояние между направлениями на центральный максимум (θ = 0) и направлением на первый (ближайший ц центральному максимуму) минимум интенсивности: δθ = θ1min:
При малых углах θ: sinθ1min ≈ θ1min, поэтому угловая ширина центрального (и ближайших к нему) главного максимума:

6.5 Дифракционная решетка
ЛЕКЦИЯ 6. ДИФРАКЦИЯ СВЕТА

Дифракционная решетка
Дифракционная решетка представляет собой совокупность большого количества одинаковых, расположенных на одинаковом расстоянии друг от друга длинный щелей в непрозрачном экране.
Периодом (постоянной) решетки d называется расстояние между серединами соседних щелей.
Дифракция света, прошедшего через решетку, – это дифракция Фраунгофера.

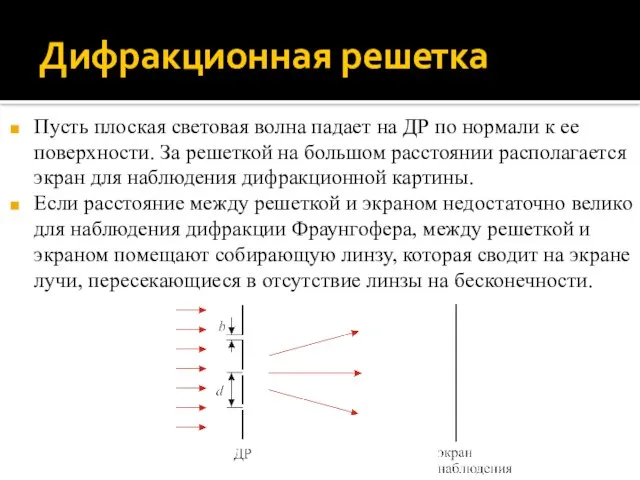
Дифракционная решетка
Пусть плоская световая волна падает на ДР по нормали к ее поверхности. За решеткой на большом расстоянии располагается экран для наблюдения дифракционной картины.
Если расстояние между решеткой и экраном недостаточно велико для наблюдения дифракции Фраунгофера, между решеткой и экраном помещают собирающую линзу, которая сводит на экране лучи, пересекающиеся в отсутствие линзы на бесконечности.

Дифракционная решетка
Пусть период решетки равен d, ширина каждой щели b, число щелей N. Определим угловое распределение интенсивности света на экране после прохождения решетки.
Рассмотрим сначала одну отдельную щель ширины b. Обозначим I1(θ) – интенсивность света, испускаемого поверхностью щели в направлении θ.
Ранее была получена формула для I1(θ):

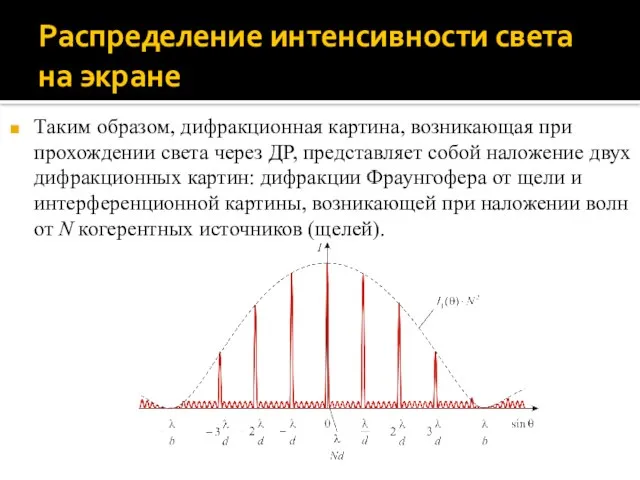
Распределение интенсивности света на экране
Пусть теперь свет падает на решетку, состоящую из N щелей – N когерентных источников света, расположенных на расстоянии d друг от друга.
Тогда интенсивность I(θ) результирующей световой волны, возникающей в результате наложения волн от N источников:

Распределение интенсивности света на экране
Таким образом, дифракционная картина, возникающая при прохождении света через ДР, представляет собой наложение двух дифракционных картин: дифракции Фраунгофера от щели и интерференционной картины, возникающей при наложении волн от N когерентных источников (щелей).

Свойства дифракционной решетки
Перечислим основные особенности дифракционной картины от ДР.
1) Углы θ, определяющие направления на главные интерференционные максимумы, удовлетворяют условию, аналогичному рассмотренному в предыдущем параграфе:
2) Угловая полуширина главного максимума при небольших m:
3) Интенсивность света Imax в главном максимуме ДР в N2 раз превышает интенсивность I1 света, испускаемого одной отдельно расположенной щелью: Imax = N2.

Свойства дифракционной решетки
4) Предельный (наибольший возможный) порядок главного максимума mпред в дифракционной картине зависит от геометрических размеров решетки
Из условия главных максимумов найдем:
Таким образом, mпред равен целому числу длин волн λ, укладывающихся на расстоянии d. Период решетки равен наибольшей возможной оптической разности хода интерферирующих лучей, идущих от двух соседних щелей. При этом лучи распространяются вдоль поверхности ДР (θ = π/2).

6.6 Дифракционная решетка как спектральный прибор
ЛЕКЦИЯ 6. ДИФРАКЦИЯ СВЕТА

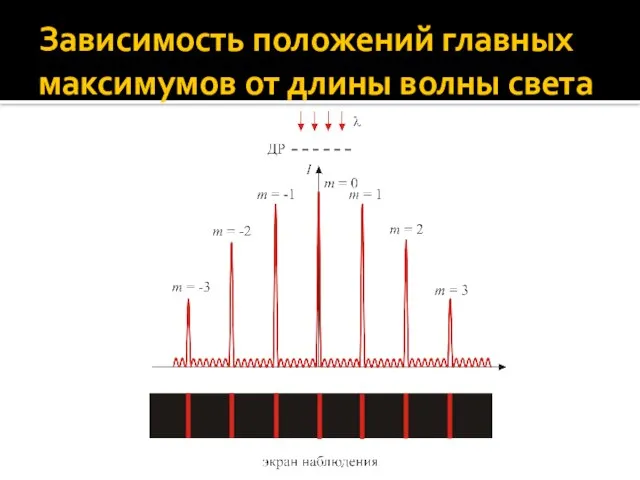
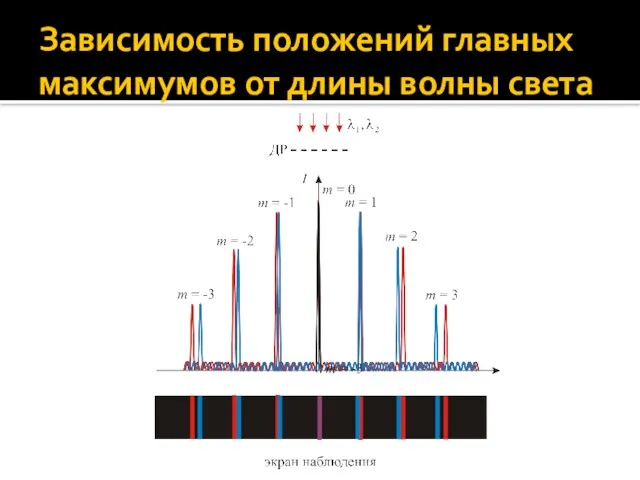
Зависимость положений главных максимумов от длины волны света
При нормальном падении света с длиной волны λ на ДР положение в пространстве главных максимумов интенсивности в дифракционной картине определяется условием:
Здесь d – период решетки, m = 0, ±1, ±2, … - порядок главного максимума, θ – угол между нормалью к поверхности ДР и направлением на главный максимум.

Зависимость положений главных максимумов от длины волны света
Направления на главный максимум (угол θ) и положения максимума на экране зависят от длины волны λ: чем больше λ, тем больше угол θ и тем дальше от центра дифракционной картины располагается соответствующий максимум интенсивности.
От длины волны λ не зависит положение только одного главного максимума – центрального (при m = 0, θ = 0 для любых λ)

Зависимость положений главных максимумов от длины волны света

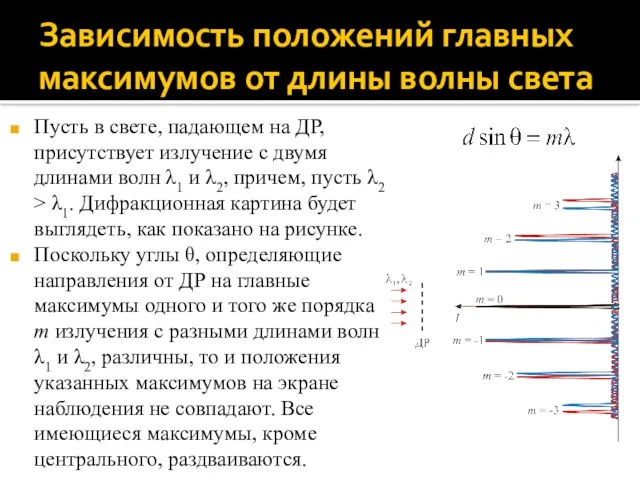
Зависимость положений главных максимумов от длины волны света
Пусть в свете, падающем на ДР, присутствует излучение с двумя длинами волн λ1 и λ2, причем, пусть λ2 > λ1. Дифракционная картина будет выглядеть, как показано на рисунке.
Поскольку углы θ, определяющие направления от ДР на главные максимумы одного и того же порядка m излучения с разными длинами волн λ1 и λ2, различны, то и положения указанных максимумов на экране наблюдения не совпадают. Все имеющиеся максимумы, кроме центрального, раздваиваются.

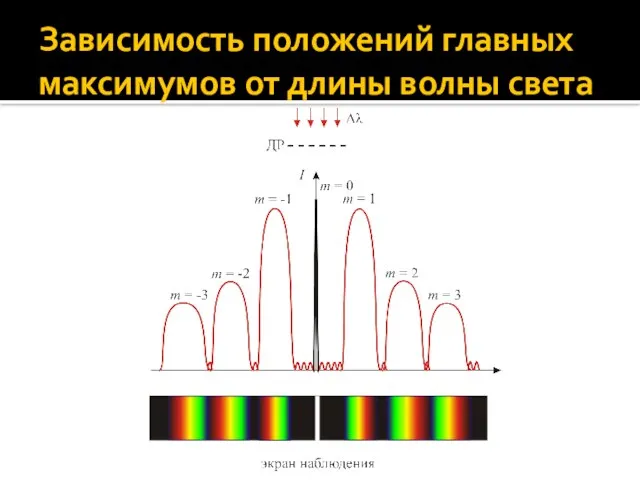
Зависимость положений главных максимумов от длины волны света

Зависимость положений главных максимумов от длины волны света
Если пропускать через ДР белый свет, то каждый максимум m-го порядка в дифракционной картине будет представлять собой совокупность смещенных один относительно другого вдоль экрана наблюдения дифракционных максимумов этого же порядка, каждый из которых соответствует определенной длине волны излучения.
Совокупность всех максимумов m-го порядка, соответствующих разным длинам волн, образует окрашенную в разные цвета – от фиолетового до красного – полосу, причем ее фиолетовый край располагается ближе к центру дифракционной картины, чем красный.

Зависимость положений главных максимумов от длины волны света
ОШИБКА !!!

Дисперсионная область дифракционной решетки
Дисперсионной областью Δλ спектрального прибора называется наибольший интервал длин волн света, который с помощью данного прибора может быть разложен в спектр.
Ограничение ширины спектрального интервала Δλ при использовании ДР в качестве спектрального прибора обусловлено следующим обстоятельством. Если интервал Δλ слишком велик, то в дифракционной картине максимум m-го порядка излучения с наибольшей имеющейся длиной волны перекрывается с максимумом (m + 1)-го порядка с наименьшей длиной волны. В этих условиях наблюдение спектра становится невозможным (говорят, что спектры m-го и (m + 1)-го порядков не разрешаются).

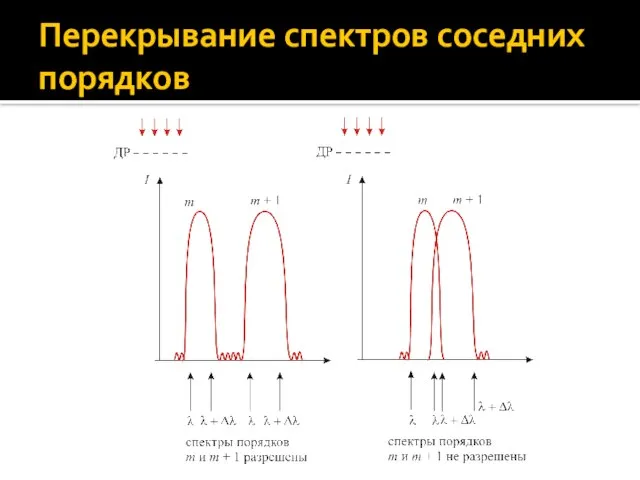
Перекрывание спектров соседних порядков

Дисперсионная область дифракционной решетки
Обозначим: λ и λ + Δλ – соответственно наименьшая и наибольшая длины волн в падающем на ДР свете. Тогда ширина спектрального интервала равна Δλ.
Запишем условия главных максимумов, определяющие углы θλ+Δλ и θλ, определяющие направления на максимумы m-го порядка дли излучения с длиной волны λ + Δλ и (m + 1)-го порядка дли излучения с длиной волны λ:
Если рассматриваемые максимумы перекрываются, то θλ+Δλ = θλ и тогда m(λ + Δλ) = (m + 1)λ, откуда находим значение Δλ, при котором начинается перекрывание максимумов интенсивности соседних порядков в дифракционной картине: Δλ = λ/m

Дисперсионная область дифракционной решетки
Выражение Δλ = λ/m определяет дисперсионную область дифракционной решетки. Она зависит от порядка m главного максимума, который используется для получения спектра: с ростом m дисперсионная область уменьшается, т.е. перекрывание спектров соседних порядков наступает раньше – при меньшей ширине спектрального интервала Δλ пропускаемого через ДР света.
Зная ширину спектрального интервала Δλ падающего на решетку света, можно оценить порядок главного максимума m, наиболее удобный для наблюдения спектра.

Ограничение порядка спектра дисперсионной областью ДР
Пусть например, белый свет содержит волны в диапазоне от 400 до 760 нм, т.е. Δλ = 360 нм. Тогда порядок главного максимума, который начинает перекрываться с соседним (m + 1)-м максимумом равен:
Следовательно, разложение белого света в спектр с помощью дифракционной решетки возможно лишь в первом или, в крайнем случае, втором порядке главного максимума.

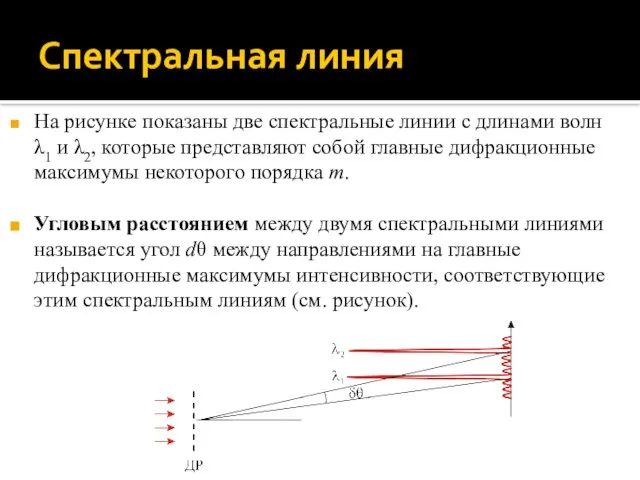
Спектральная линия
В зависимости от природы источника света спектр электромагнитного излучения – набор характеризующих излучение частот или длин волн – может быть непрерывным или дискретным.
Дискретный спектр, наблюдаемый с помощью дифракционной решетки, представляется в виде системы окрашенных (каждый в определенный цвет) главных максимумов интенсивности в дифракционной картине.
Спектральной линией называется излучение с определенной длиной волны, а также соответствующая этому излучению дифракционный максимум интенсивности света в виде окрашенной в определенный цвет полосы на экране наблюдения.

Спектральная линия
На рисунке показаны две спектральные линии с длинами волн λ1 и λ2, которые представляют собой главные дифракционные максимумы некоторого порядка m.
Угловым расстоянием между двумя спектральными линиями называется угол dθ между направлениями на главные дифракционные максимумы интенсивности, соответствующие этим спектральным линиям (см. рисунок).

Угловая дисперсия дифракционной решетки
Обозначим через dθ угловое расстояние между двумя спектральными линиями с близкими друг другу длинами волн λ1 и λ2, а через dλ = λ2 – λ1 – разность длин вон этих линий.
Угловой дисперсией D называется величина, равна угловому расстоянию между двумя спектральными линиями, длины волн которых отличаются на единицу:
Вычислим угловую дисперсию решетки.

Угловая дисперсия дифракционной решетки
Продифференцируем обе части равенства, определяющего направления на главные максимумы интенсивности света: dsinθ = mλ:
При разложении света в спектр с помощью ДР, как правило, используются максимумы не слишком высокого порядка, что соответствует малым углам θ. Тогда cosθ ≈ 1, так что угловая дисперсия решетки приблизительно равна:

Разрешающая способность спектрального прибора
Разрешающей силой (способностью) спектрального прибора, в частности, дифракционной решетки, называется величина
Здесь δλmin – наименьшая разность длин волн двух спектральных линий, при которой эти линии воспринимаются раздельно (т.е. разрешаются); λ – длина волны одной из линий или средняя из них.

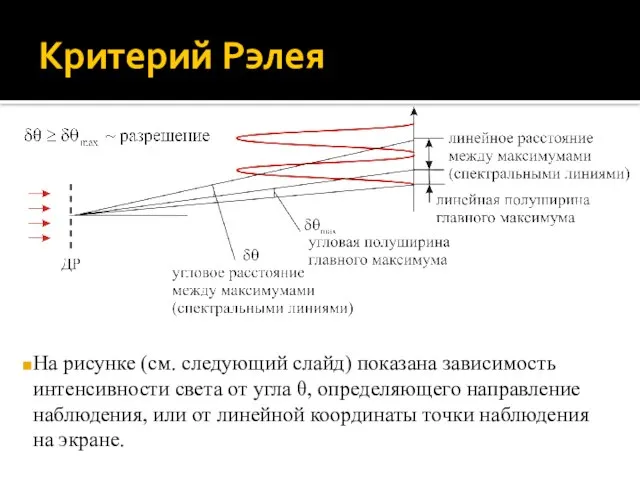
Критерий Рэлея
Критерий разрешения Рэлея. Две спектральные линии воспринимаются раздельно (разрешаются), если расстояние между соответствующими этим линиям максимумами интенсивности света в дифракционной картине равно полуширине каждого максимума.
Развернутая формулировка критерия спектрального разрешения Рэлея: две спектральные линии с близкими длинами волн λ1 и λ2 считаются разрешенными, если главный максимум дифракционной картины для одной длины волны совпадает по своему положению с первым дифракционным минимумом в том же порядке для другой длины волны.

Критерий Рэлея
На рисунке (см. следующий слайд) показана зависимость интенсивности света от угла θ, определяющего направление наблюдения, или от линейной координаты точки наблюдения на экране.

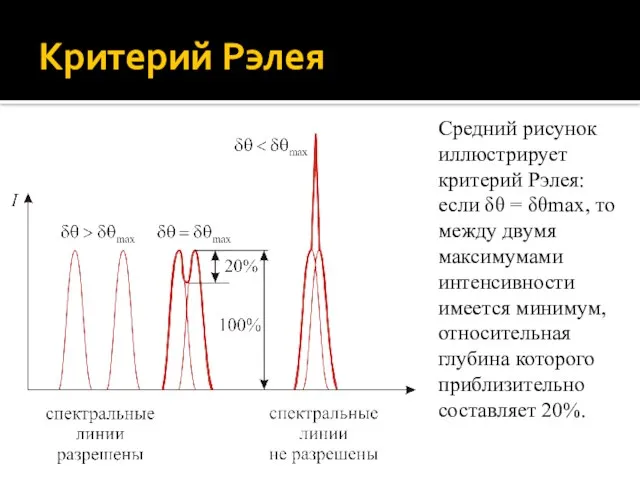
Критерий Рэлея
Средний рисунок иллюстрирует критерий Рэлея: если δθ = δθmax, то между двумя максимумами интенсивности имеется минимум, относительная глубина которого приблизительно составляет 20%.