Содержание
- 2. Требования государственного образовательного стандарта 1.4. Квалификационная характеристика выпускника 1.4.1. Объекты профессиональной деятельности - … предприятия по
- 3. Требования государственного образовательного стандарта 1.4.4. Квалификационные требования Инженер должен знать: Основные требования, предъявляемые к … материалам,
- 4. Сопротивление материалов: основные понятия; метод сечений; центральное растяжение-сжатие; сдвиг; геометрические характеристики сечений; прямой поперечный изгиб; кручение;
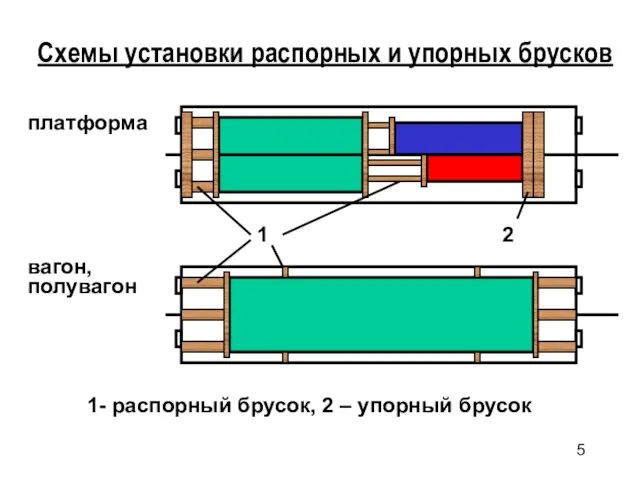
- 5. Схемы установки распорных и упорных брусков 1- распорный брусок, 2 – упорный брусок платформа вагон, полувагон
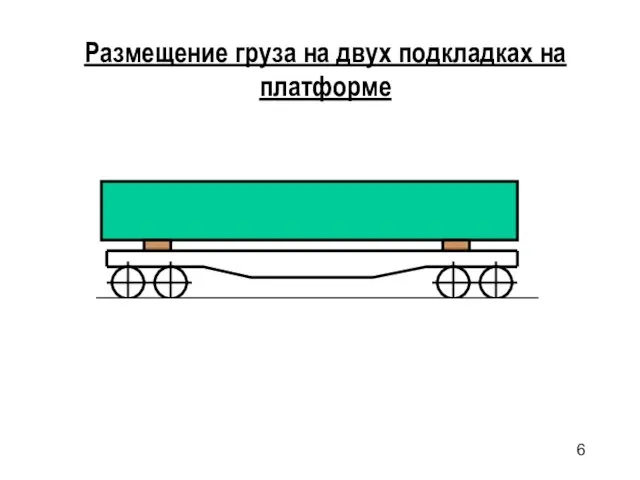
- 6. Размещение груза на двух подкладках на платформе
- 7. Литература 1. Ахметзянов М.Х., Лазарев И.Б. Сопротивление материалов. СГУПС, 1997. 2. Задания по сопротивлению материалов. Часть
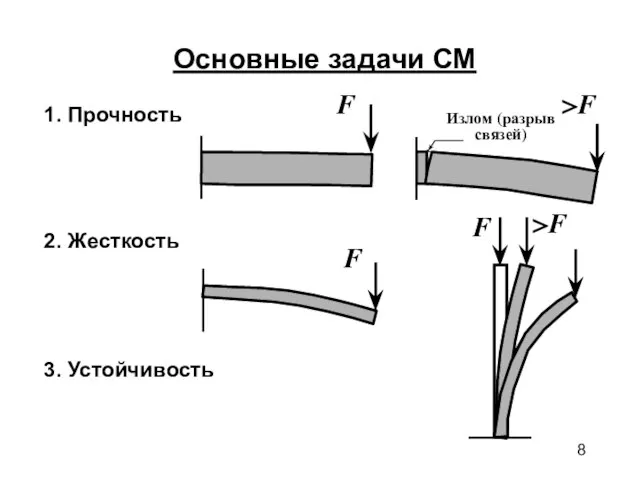
- 8. Основные задачи СМ 2. Жесткость F
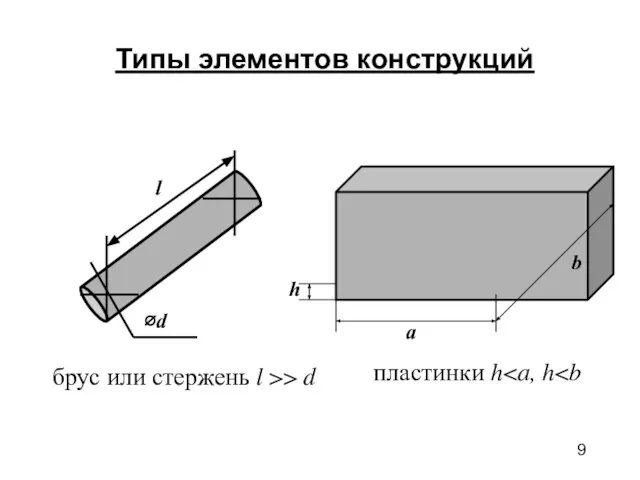
- 9. Типы элементов конструкций пластинки h брус или стержень l >> d
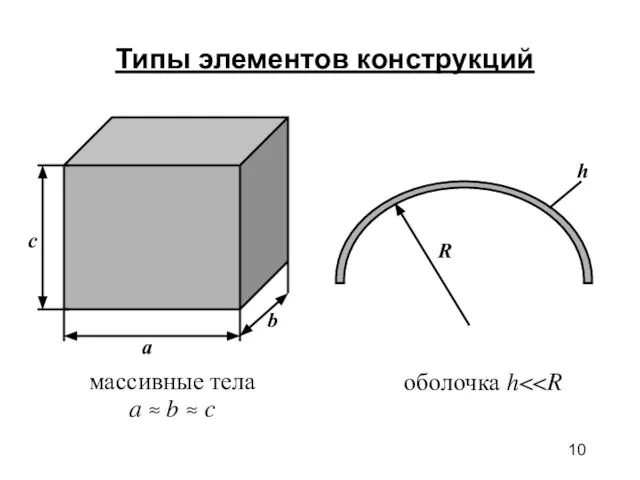
- 10. оболочка h массивные тела a ≈ b ≈ c Типы элементов конструкций
- 11. Основные гипотезы Сплошность – непрерывность пространства тела, хотя тела имеют дискретное (атомарное) строение. Однородность – независимость
- 12. Классификация сил Внешние и внутренние Статические и динамические Постоянные и временные
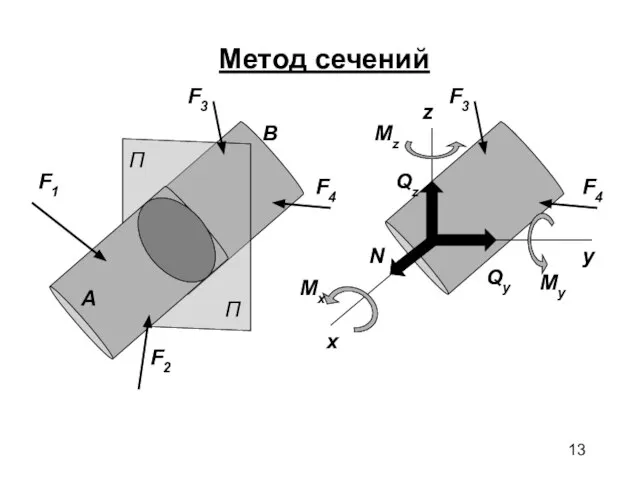
- 13. Метод сечений A B x y z
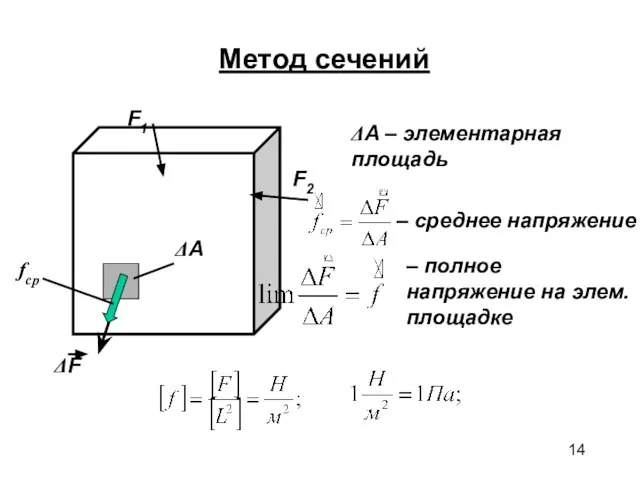
- 14. Метод сечений ΔA – элементарная площадь – среднее напряжение
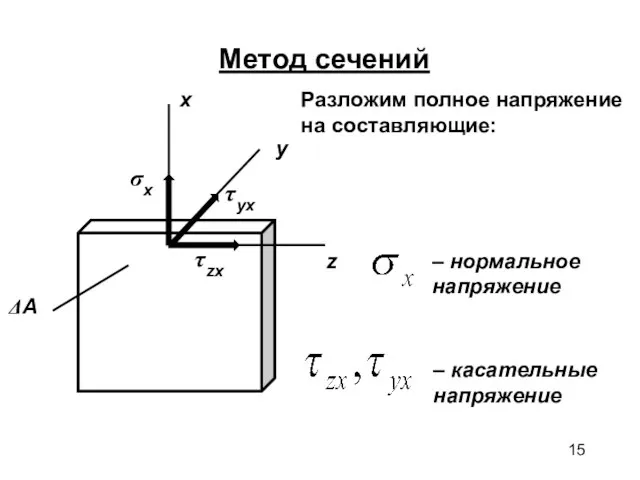
- 15. x y z Метод сечений Разложим полное напряжение на составляющие:
- 16. Растяжение (сжатие) прямых стержней Деформацией растяжения (сжатия) прямого стержня называется такой случай сопротивления стержня, когда внутренние
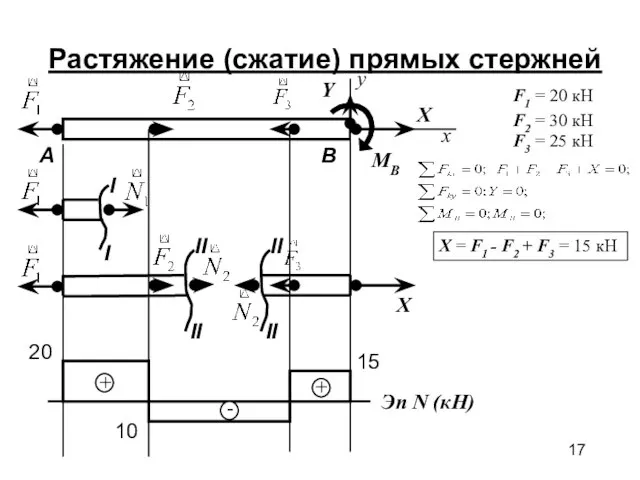
- 17. Растяжение (сжатие) прямых стержней x y X Y MB F1 = 20 кН F2 = 30
- 18. Растяжение (сжатие) прямых стержней Правило: Продольная сила равна сумме проекций всех внешних сил, взятых по одну
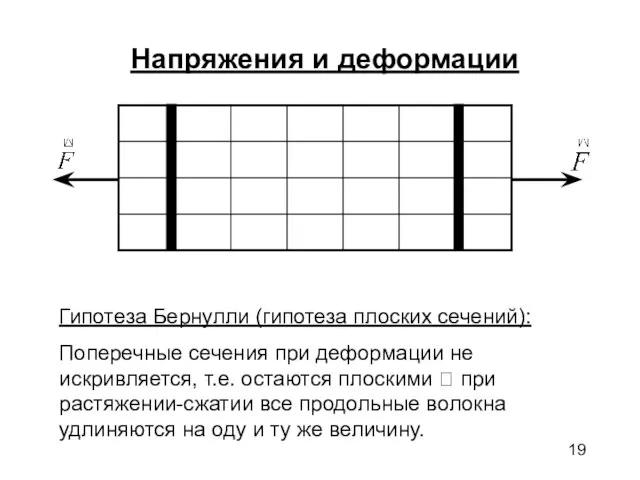
- 19. Напряжения и деформации Гипотеза Бернулли (гипотеза плоских сечений): Поперечные сечения при деформации не искривляется, т.е. остаются
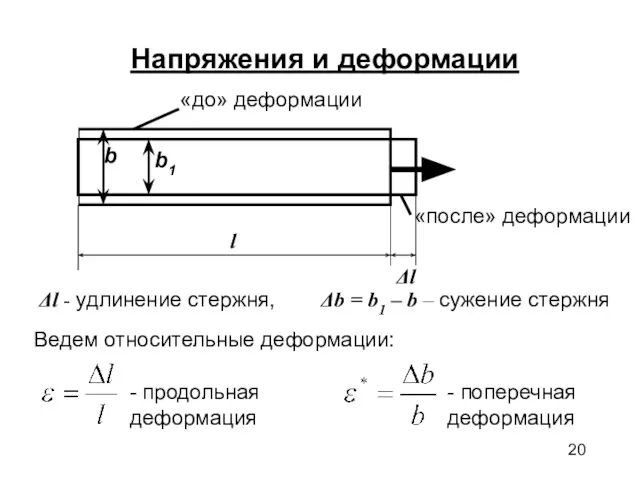
- 20. Напряжения и деформации Δl - удлинение стержня, Δb = b1 – b – сужение стержня Ведем
- 21. Напряжения и деформации Сталь: ν ~ 0.25 …0.3 Медь: ν ~ 0.4 Бетон: ν ~ 0.15
- 22. Напряжения и деформации В 1676 году Роберт Гук экспериментально установил σx = Eε E – модуль
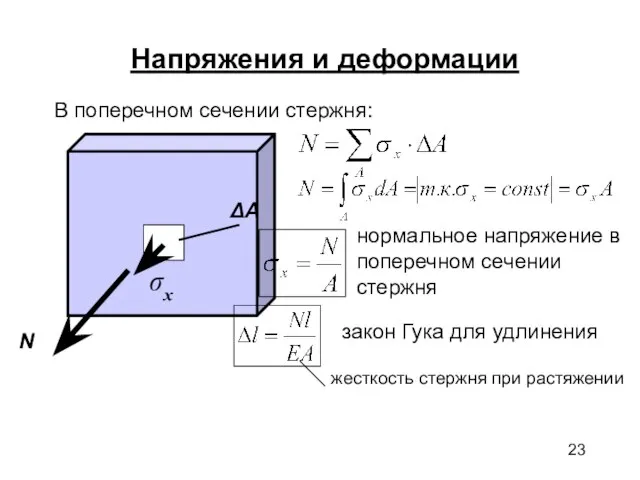
- 23. Напряжения и деформации В поперечном сечении стержня:
- 25. Скачать презентацию










 Идеальный компрессор
Идеальный компрессор Колебательный контур. Электромагнитные колебания. Принцип радиосвязи и телевидения
Колебательный контур. Электромагнитные колебания. Принцип радиосвязи и телевидения Физика космоса, кружок. Космология в ОТО
Физика космоса, кружок. Космология в ОТО Презентация на тему Законы постоянного тока (10 класс)
Презентация на тему Законы постоянного тока (10 класс)  Физическая лихорадка. Методические указания
Физическая лихорадка. Методические указания Выбор подходящего трансмиссионного масла
Выбор подходящего трансмиссионного масла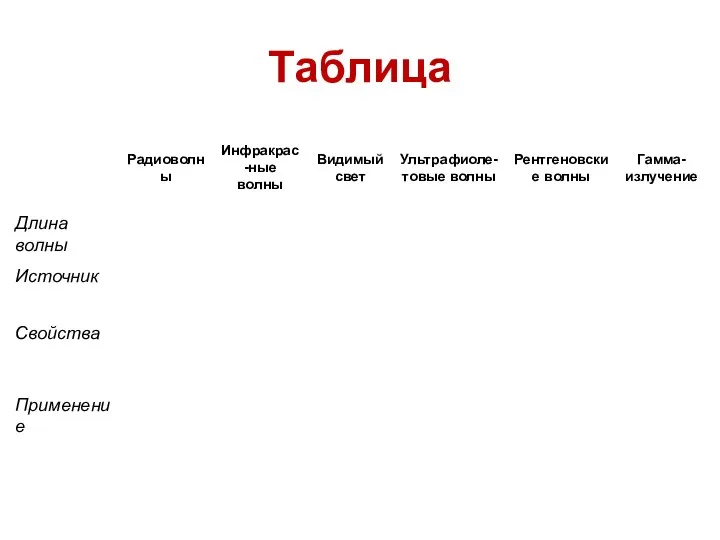 Радиоволны. Таблица. 9 класс
Радиоволны. Таблица. 9 класс Электростатика. Проводники и диэлектрики
Электростатика. Проводники и диэлектрики Нефтегазовая и рудная геофизика. Сейсмические методы при изучении строения земной коры
Нефтегазовая и рудная геофизика. Сейсмические методы при изучении строения земной коры Вычисление силы тяжести
Вычисление силы тяжести Презентация на тему Снег
Презентация на тему Снег  Импульс материальной точки. Другая формулировка второго закона Ньютона
Импульс материальной точки. Другая формулировка второго закона Ньютона Computer modeling of motion of globular clusters in gravitational field
Computer modeling of motion of globular clusters in gravitational field Машины переменного тока. Переменный ток. Синхронные генераторы
Машины переменного тока. Переменный ток. Синхронные генераторы Дробилка безрешетная
Дробилка безрешетная Подстанция переменного тока Промузел 110/35/6 кВ
Подстанция переменного тока Промузел 110/35/6 кВ Температура. Факты и немного о теплообмене
Температура. Факты и немного о теплообмене Основы взаимозаменяемости и технические измерения
Основы взаимозаменяемости и технические измерения Основные сведения о строении атома
Основные сведения о строении атома Электропроводность полупроводников
Электропроводность полупроводников Презентация на тему Фундаментальные взаимодействия
Презентация на тему Фундаментальные взаимодействия  Закон всемирного тяготения
Закон всемирного тяготения Трехфазные электрические цепи. Основные положения. Лекция 09
Трехфазные электрические цепи. Основные положения. Лекция 09 Бином Ньютона. Треугольник Паскаля
Бином Ньютона. Треугольник Паскаля Велоподготовка для дальних поездок
Велоподготовка для дальних поездок Механические волны
Механические волны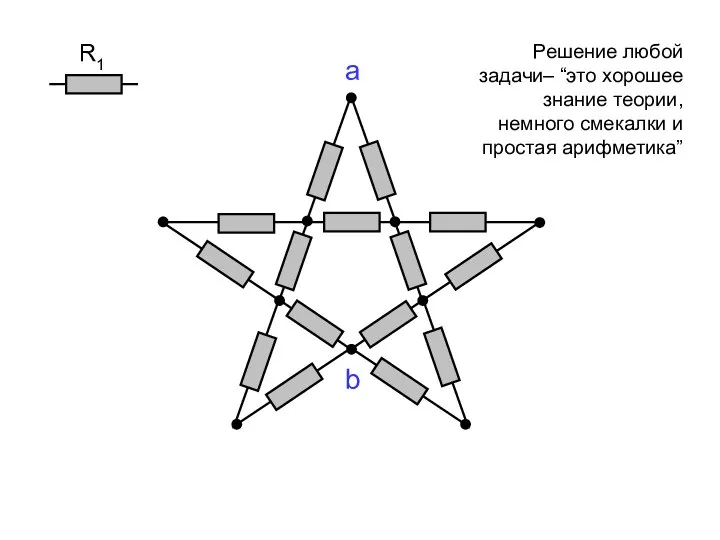 Решение задач на расчет электрических цепей
Решение задач на расчет электрических цепей Параллельная работа двух одинаковых центробежных насосов
Параллельная работа двух одинаковых центробежных насосов