Содержание
- 2. Хочешь быть умным, научись разумно спрашивать, внимательно слушать, спокойно отвечать и переставать говорить, когда нечего сказать.
- 3. Содержание
- 4. Законы математики, имеющие какое-либо отношение к реальному миру, ненадежны, а надежные математические законы не имеют отношения
- 5. Вероятность Буквы Б,А,Б,У,Ш,К,А складывают в мешок и вынимают оттуда в произвольном порядке. Найдите вероятность того, что
- 6. Таким образом вероятность равна 4/5040=1/1260
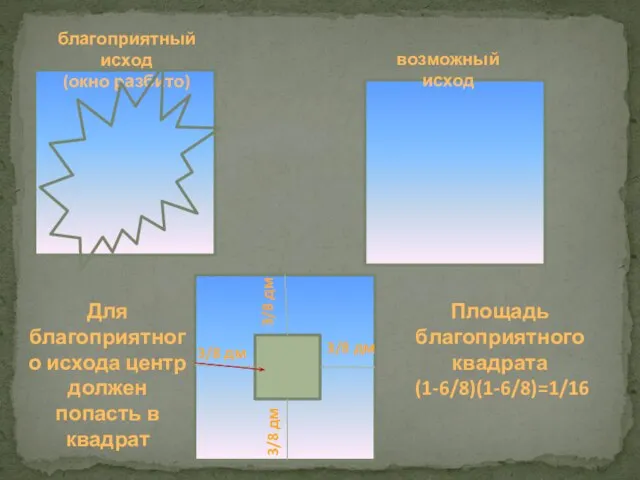
- 7. Хулиган Вася После уроков хулиган Вася решил бросать круглый камень диаметром 0,75 дм в окно защищенное
- 8. благоприятный исход (окно разбито) возможный исход Для благоприятного исхода центр должен попасть в квадрат 3/8 дм
- 9. Игральные кубики Найдите, вероятность того, что при одновременном бросании двух кубиков сумма на их гранях будет
- 10. Немного истории Найдем вероятность выпадения герба на монете: Равновозможных исходов: 2 Благоприятных исходов: 1 Итого: ½
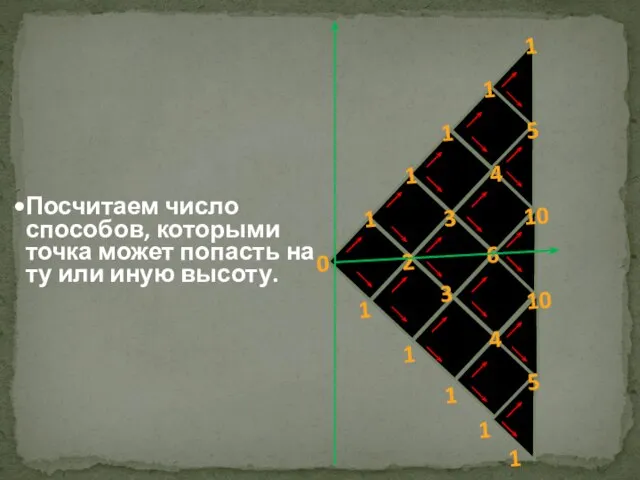
- 11. Рассмотрим задачу: за один шаг точка (частица) продвинется на 1 вниз или на 1 вверх. На
- 13. Блуждание такого рода осуществляется в специальном приборе – доска Гальтона В меню
- 14. Треугольник Паскаля (прямоугольный) Принцип построения таблицы таков: в каждой клетке стоит сумма числа над ним и
- 15. Формула бинома Ньютона и треугольник Паскаля. Действительно, 1 1 1 1 2 1 1 3 3
- 16. Проведем эксперимент У нас есть 16 различных траекторий блуждания точки для 4 шагов. Пронумеруем их от
- 17. Гарднер о треугольнике Паскаля История о треугольнике …? Немного «волшебства»
- 18. В.А.Успенский «Треугольник Паскаля» М. «Наука». Главная редакция физико-математической литературы, 1979 А.Н.Колмогоров и др. «Введение в теорию
- 19. Определения вероятности При классическом определении вероятность события определяется равенством Р(А)=m/n, где n – число равновозможных исходов,
- 20. Назад
- 21. Геометрическая вероятность Пусть плоская фигура g составляет часть плоской фигуры G. На фигуру G наугад брошена
- 22. Назад
- 23. Треугольник Паскаля (равнобедренный) Назад
- 24. Назад
- 25. Пример перевода в двоичную систему счисления числа 10: 10:2=5 (остаток 0) 5:2=2 (остаток 1) 2:2=1 (остаток
- 26. Назад
- 27. Мартин Гарднер: Треугольник Паскаля так прост, что выписать его сможет даже десятилетний ребенок. В тоже время
- 28. Назад
- 29. Немного истории: Первое упоминание треугольной последовательности биномиальных коэффициентов встречается в комментарии индийского математика X в. Халаюдхи.
- 30. Назад
- 31. 1 1 1 1 2 1 1 3 3 1 1 4 6 4 1 1
- 32. Треугольные числа Назад Цифры (числа) не управляют миром, но они показывают, как управляется мир. И. Гете
- 33. 1 1 1 2 1 1 3 3 1 1 4 6 4 1 1 5
- 34. Все внутренние члены m-й строки Паскаля делятся на m тогда и только тогда, когда m-простое. Назад
- 35. Узоры треугольника Паскаля Назад
- 36. Назад
- 37. Перестановки Перестановкой из n элементов называется каждое расположение этих элементов в определенном порядке. Число возможных перестановок
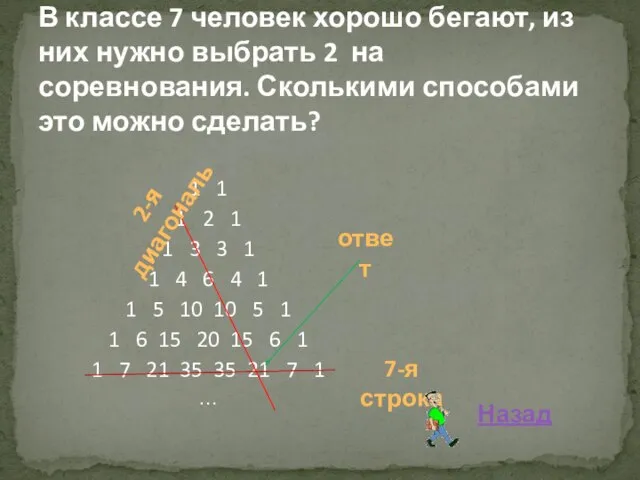
- 38. 10 молодых людей пришли в ресторан, но никак не могли усесться вокруг стола, тогда официант предложил
- 40. Скачать презентацию

































 Квантовая радиофизика
Квантовая радиофизика Геострофическая адвекция температуры
Геострофическая адвекция температуры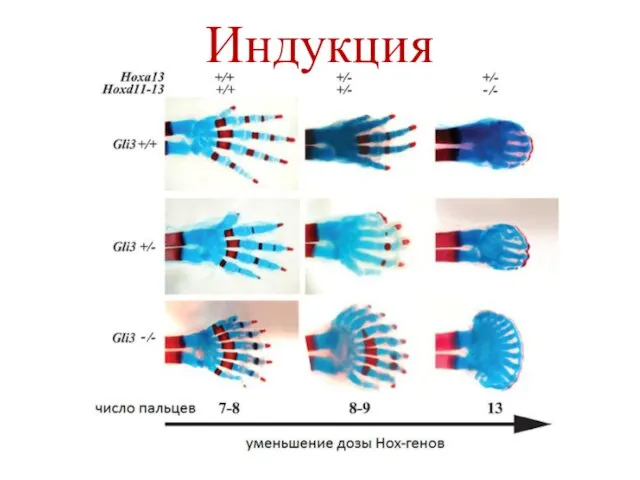 Индукция
Индукция Элементарные частицы. Античастицы
Элементарные частицы. Античастицы Развитие двигателя внутреннего сгорания
Развитие двигателя внутреннего сгорания Плавание тел
Плавание тел Будем знакомы – физика!
Будем знакомы – физика! Определение скоростей точек тела при плоскопараллельном движении
Определение скоростей точек тела при плоскопараллельном движении Дефлектор
Дефлектор Динамика
Динамика Оптика. Корпускулярно-волновой дуализм
Оптика. Корпускулярно-волновой дуализм Агрегатные состояния вещества
Агрегатные состояния вещества Градиент и его свойства
Градиент и его свойства Otáčavé účinky sily
Otáčavé účinky sily Постоянный электрический ток
Постоянный электрический ток Техническое обслуживание, диагностирование и ремонт жидкостной системы охлаждения автомобильного двигателя
Техническое обслуживание, диагностирование и ремонт жидкостной системы охлаждения автомобильного двигателя Презентация на тему Методы наблюдения и регистрации элементарных частиц
Презентация на тему Методы наблюдения и регистрации элементарных частиц  Равновесие тел. Решение задач
Равновесие тел. Решение задач Магнітне поле (Лекція 1)
Магнітне поле (Лекція 1) Методы измерения потерь в оптических волокнах
Методы измерения потерь в оптических волокнах Подсистема управления маршрутами общественного транспорта
Подсистема управления маршрутами общественного транспорта Распределение Максвелла
Распределение Максвелла Гидротрансформатор (турботрансформатор)
Гидротрансформатор (турботрансформатор) Связь физики и схемотехники
Связь физики и схемотехники Волновые явления (11 класс)
Волновые явления (11 класс) Теоретические основы электротехники. Трехфазные электрические цепи
Теоретические основы электротехники. Трехфазные электрические цепи Кривошипно-шатунный механизм
Кривошипно-шатунный механизм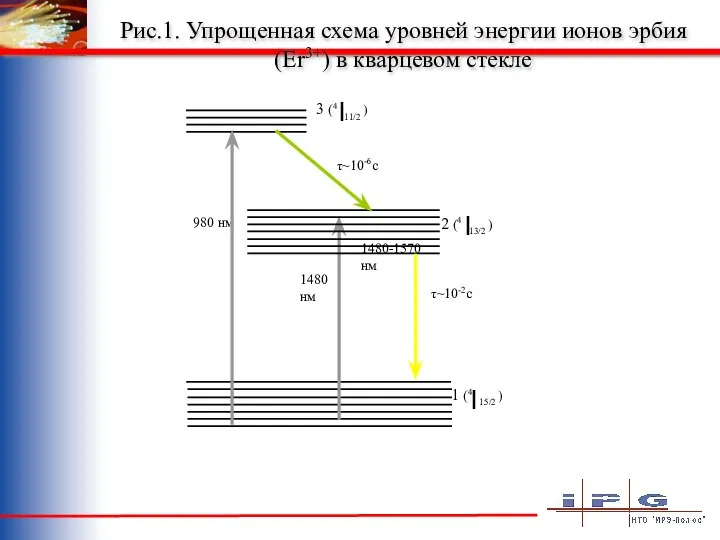 Упрощенная схема уровней энергии ионов эрбия
Упрощенная схема уровней энергии ионов эрбия