Содержание
- 2. Поток вектора напряжённости электрического поля Исходные посылки: S – поверхность, находящаяся в электрическом поле; dS –
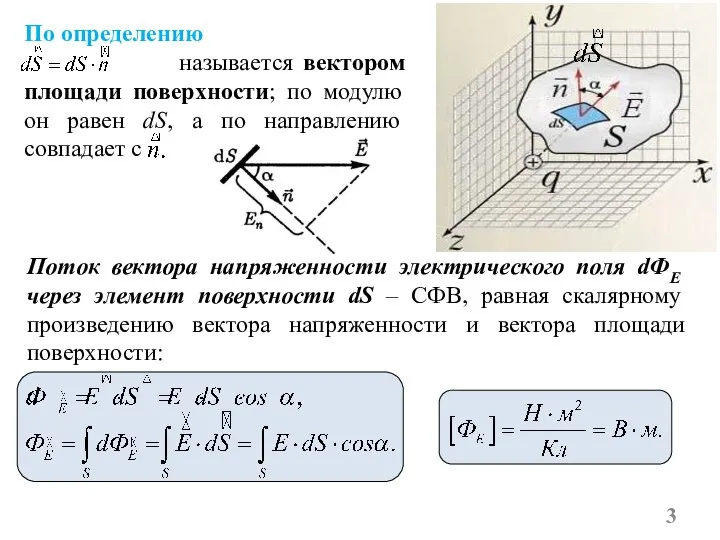
- 3. По определению называется вектором площади поверхности; по модулю он равен dS, а по направлению совпадает с
- 4. Аддитивность потока вектора напряженности электрического поля. Предположим, что N зарядов образуют электрическое поле, которое пронизывает площадь
- 5. В каких случаях легко получить аналитическое выражение для потока ФE вектора ? 1) Если вектор направлен
- 6. Поток вектора напряжённости электростатического поля в вакууме сквозь произвольную замкнутую поверхность равен алгебраической сумме заключённых внутри
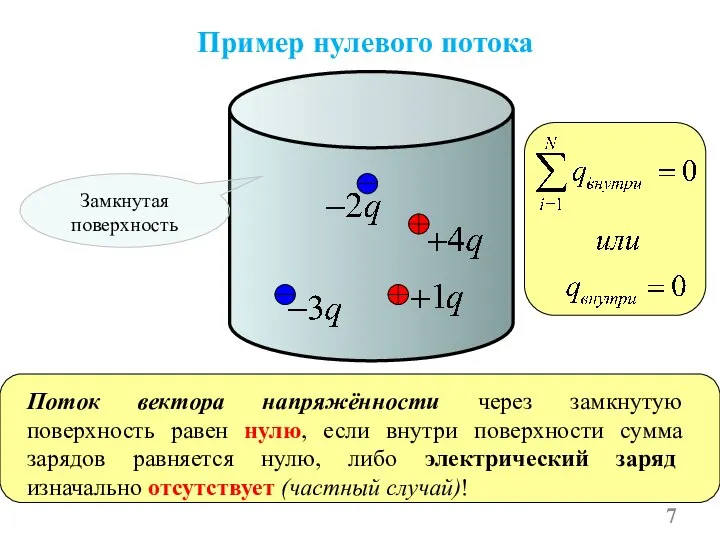
- 7. Пример нулевого потока Поток вектора напряжённости через замкнутую поверхность равен нулю, если внутри поверхности сумма зарядов
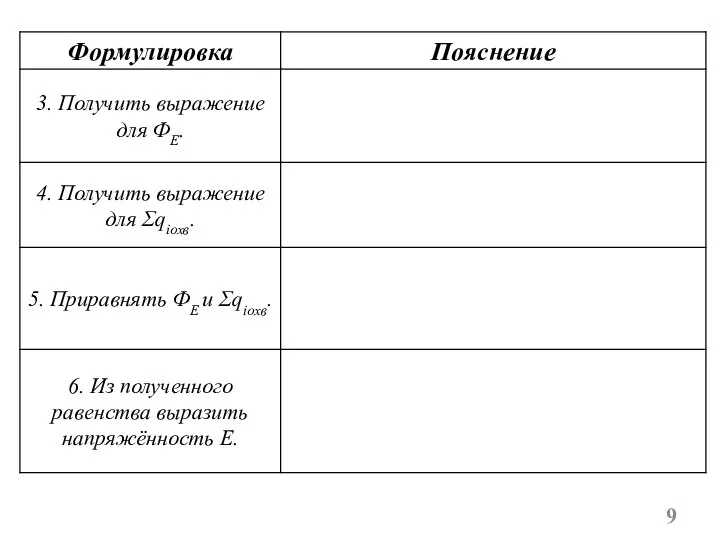
- 8. Алгоритм расчёта электрического поля с использованием теоремы Гаусса. Постановка задачи: рассчитаем напряжённость электрического поля, созданного симметричным
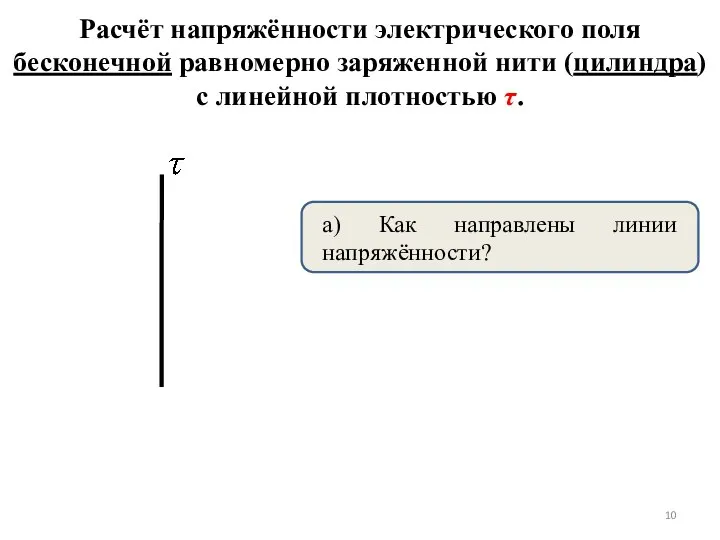
- 10. Расчёт напряжённости электрического поля бесконечной равномерно заряженной нити (цилиндра) с линейной плотностью τ. а) Как направлены
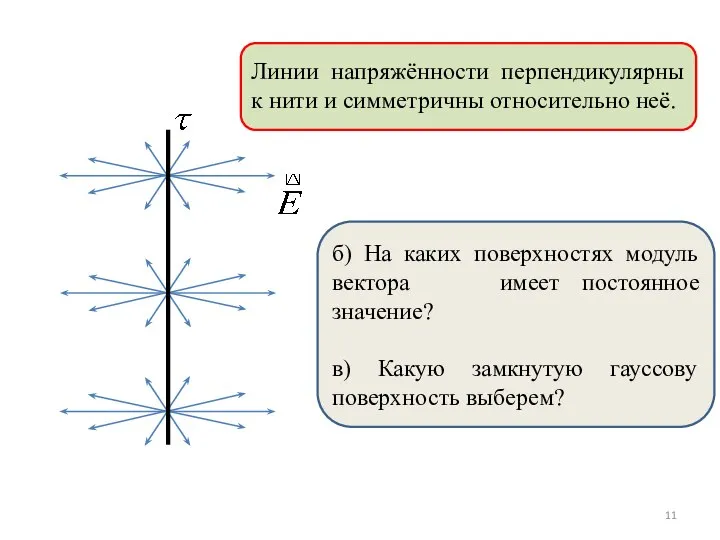
- 11. б) На каких поверхностях модуль вектора имеет постоянное значение? в) Какую замкнутую гауссову поверхность выберем? Линии
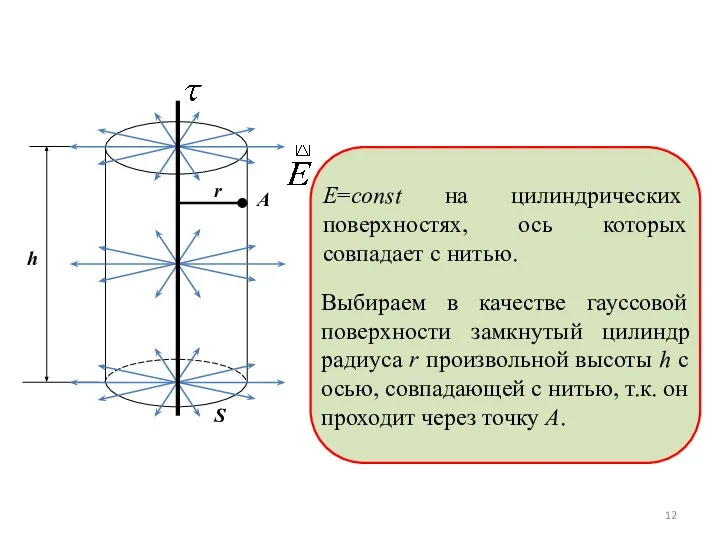
- 12. E=const на цилиндрических поверхностях, ось которых совпадает с нитью. Выбираем в качестве гауссовой поверхности замкнутый цилиндр
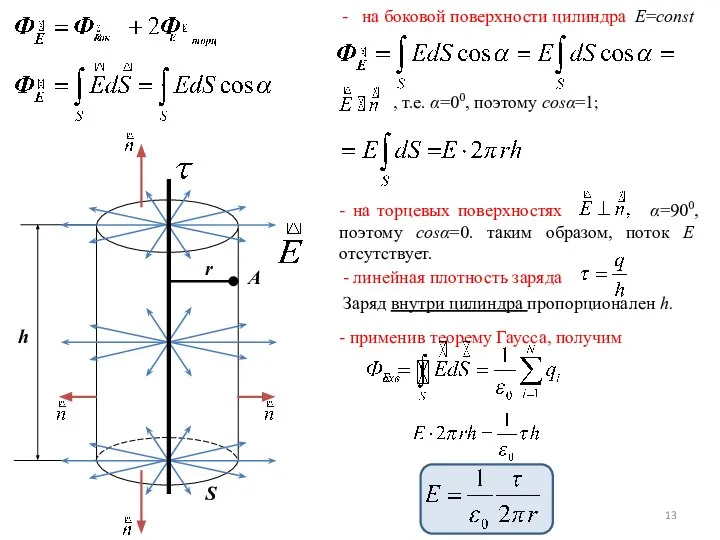
- 13. - применив теорему Гаусса, получим - линейная плотность заряда Заряд внутри цилиндра пропорционален h.
- 14. 1. Поле точечного заряда Формулы для расчета некоторых электростатических полей в вакууме Поле точечного заряда обладает
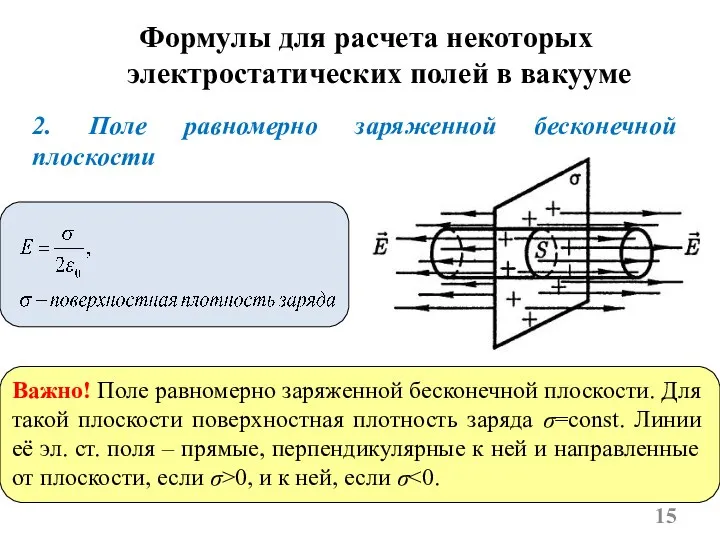
- 15. 2. Поле равномерно заряженной бесконечной плоскости Важно! Поле равномерно заряженной бесконечной плоскости. Для такой плоскости поверхностная
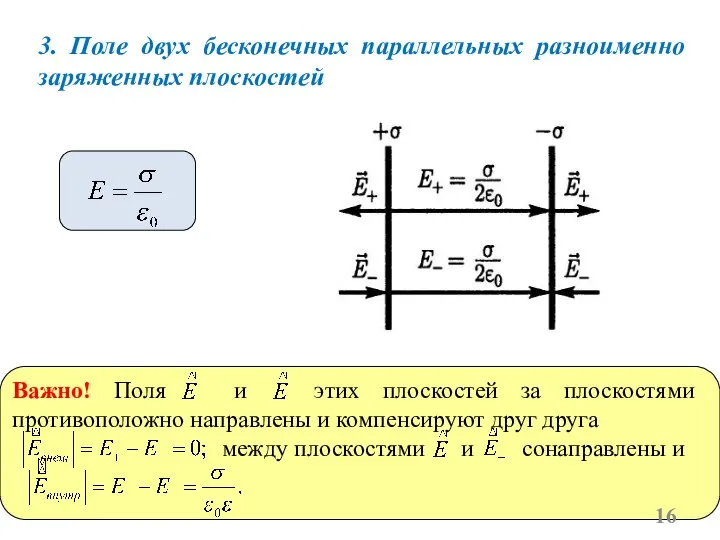
- 16. 3. Поле двух бесконечных параллельных разноименно заряженных плоскостей Важно! Поля и этих плоскостей за плоскостями противоположно
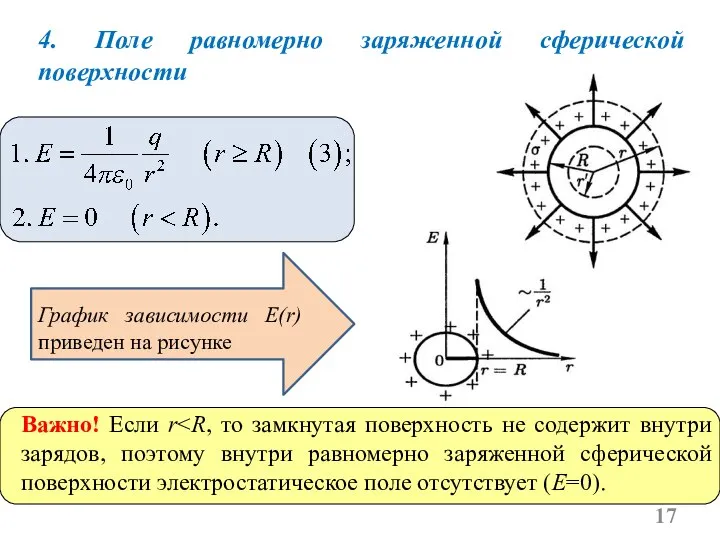
- 17. 4. Поле равномерно заряженной сферической поверхности Важно! Если r График зависимости E(r) приведен на рисунке
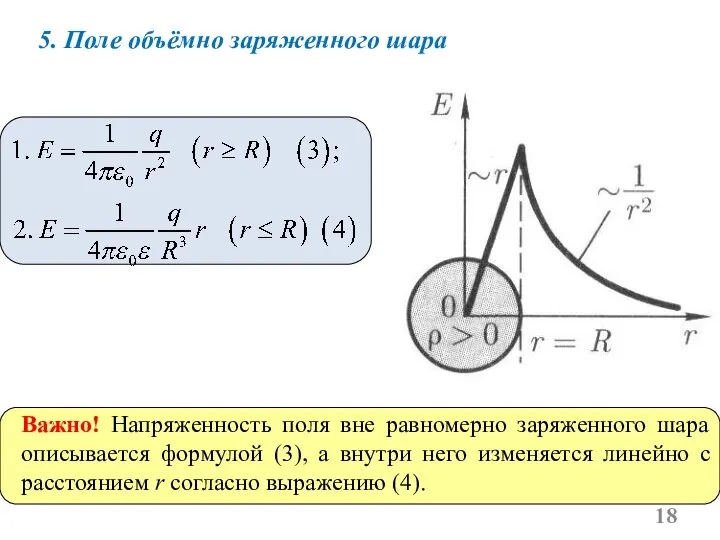
- 18. 5. Поле объёмно заряженного шара Важно! Напряженность поля вне равномерно заряженного шара описывается формулой (3), а
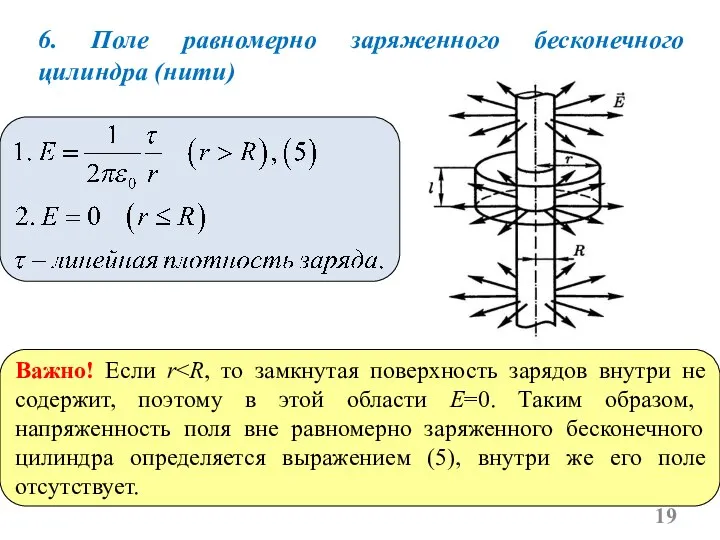
- 19. 6. Поле равномерно заряженного бесконечного цилиндра (нити) Важно! Если r
- 21. Скачать презентацию






 Строение планарных и двухслойных световодов
Строение планарных и двухслойных световодов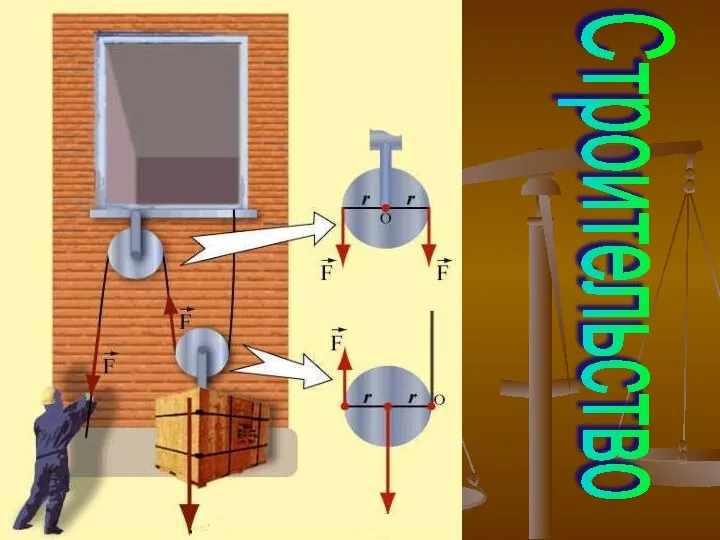 Наклонная плоскость
Наклонная плоскость Законы постоянного тока. Энергия конденсаторов.
Законы постоянного тока. Энергия конденсаторов. Текущий ремонт двигателя. Технологический процесс, оборудование и инструмент. Вопрос 19
Текущий ремонт двигателя. Технологический процесс, оборудование и инструмент. Вопрос 19 Кинематика
Кинематика Лекция
Лекция Физика и В.О.В
Физика и В.О.В Статика
Статика Изобретение радио. Принципы радиосвязи
Изобретение радио. Принципы радиосвязи Оптические приборы
Оптические приборы Решение задач на равновесие сходящейся системы сил
Решение задач на равновесие сходящейся системы сил Теория автоматического управления. Дифференцирующие звенья
Теория автоматического управления. Дифференцирующие звенья Презентация без названия
Презентация без названия Источники света. Распространение света. Отражение света
Источники света. Распространение света. Отражение света Презентация на тему Сила упрогости
Презентация на тему Сила упрогости  Спектры. Устройство спектроскопа
Спектры. Устройство спектроскопа Демонтаж трансмиссии автомобилей
Демонтаж трансмиссии автомобилей Методика организации лабораторных и экспериментальных работ учащихся на уроках физики
Методика организации лабораторных и экспериментальных работ учащихся на уроках физики Теория автоматического управления. Типовые звенья
Теория автоматического управления. Типовые звенья Резонансы в электрических цепях
Резонансы в электрических цепях Радиационный контроль дефектоскопов
Радиационный контроль дефектоскопов Закон отражения света
Закон отражения света Механическое движение (7 класс)
Механическое движение (7 класс) Презентация урока-лекции по теме «Электрическое поле точечного заряда. Закон Кулона» для профильного 10-го класса Подготовила уч
Презентация урока-лекции по теме «Электрическое поле точечного заряда. Закон Кулона» для профильного 10-го класса Подготовила уч 5 урок свободное падение тела
5 урок свободное падение тела Равноускоренное прямолинейное движение
Равноускоренное прямолинейное движение Расчет свободной энергии с помощью молекулярной динамики
Расчет свободной энергии с помощью молекулярной динамики Реверберация. Лекция2
Реверберация. Лекция2