Содержание
- 2. ЗАКОНЫ КОММУТАЦИИ
- 3. Переходным называется процесс, возникающий в электрической цепи при переходе от одного установившегося режима к другому.
- 4. При коммутации в эл. цепи возникают переходные процессы, т.е. процессы перехода тока (или напряжения) от одного
- 5. Энергия электрического поля и энергия магнитного поля могут изменяться только непрерывно, так как скачко- образное изменение
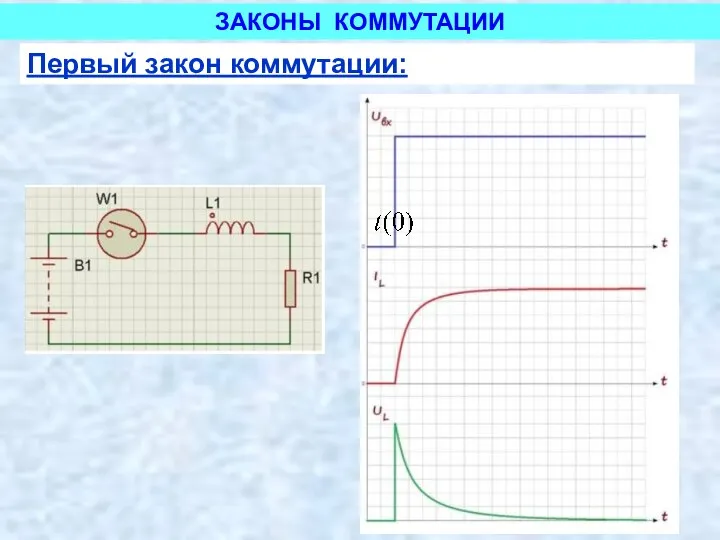
- 6. ЗАКОНЫ КОММУТАЦИИ Первый закон коммутации: В любой ветви с индуктивностью ток не может изменяться скачком и
- 7. ЗАКОНЫ КОММУТАЦИИ Первый закон коммутации:
- 8. Первый закон коммутации (обозначения):
- 9. Второй закон коммутации:
- 10. Второй закон коммутации (обозначения): uC(0+) - напряжение на емкости в момент коммутации; uC(0-) - напряжение на
- 11. Допущения, применяемые при анализе ПП 1. Полагают, что ПП длится бесконечно большое время. 2. Считается, что
- 12. Методы анализа переходных процессов в линейных цепях: 1. Классический метод 2. Операторный метод 3. Частотный метод
- 13. 1. Классический метод расчета переходных процессов заключается в непосредственном интегрировании дифференциальных уравнений, описывающих изменения токов и
- 14. 2. Операторный метод расчета переходных процессов заключается в решении системы алгебраических уравнений относительно изображений искомых переменных
- 15. 3. Частотный метод расчета переходных процессов основанный на преобразовании Фурье. Он находит широкое применение при решении
- 16. 4. Метод расчета переходных процессов с помощью итеграла Дюамеля, используется при сложной форме кривой возмущающего воздействия.
- 17. 5. Метод переменных состояния, представляет собой упорядоченный способ определения электромагнитного состояния цепи на основе решения дифференциальных
- 18. 1. Классический метод расчета переходных процессов заключается в непосредственном интегрировании дифференциальных уравнений, описывающих изменения токов и
- 19. Классический метод расчета Алгоритм: Общий случай при использовании этого метода: 1. Составляется уравнение электромагнитного состояния электрической
- 20. Связь мгновенных значений напряжений и токов на элементах электрической цепи Элемент цепи: резистор (идеальное активное сопротивление):
- 21. Связь мгновенных значений напряжений и токов на элементах электрической цепи Катушка индуктивности при наличии магнитной связи
- 22. Связь мгновенных значений напряжений и токов на элементах электрической цепи Элемент цепи: конденсатор (идеальная емкость):
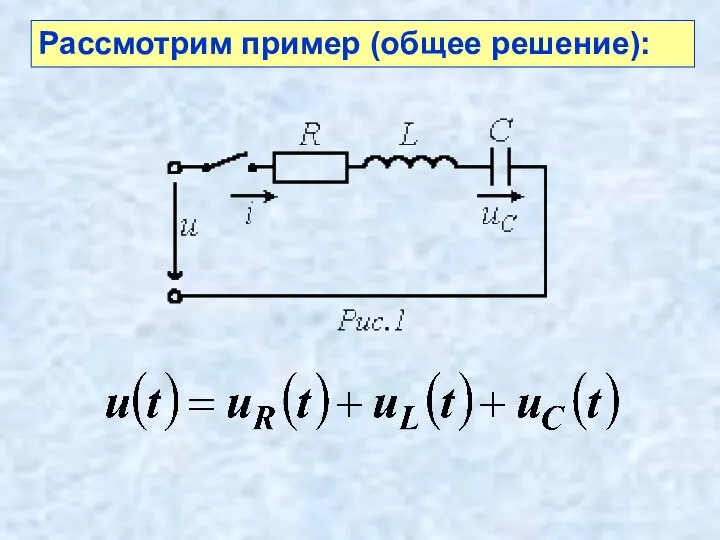
- 23. Рассмотрим пример (общее решение):
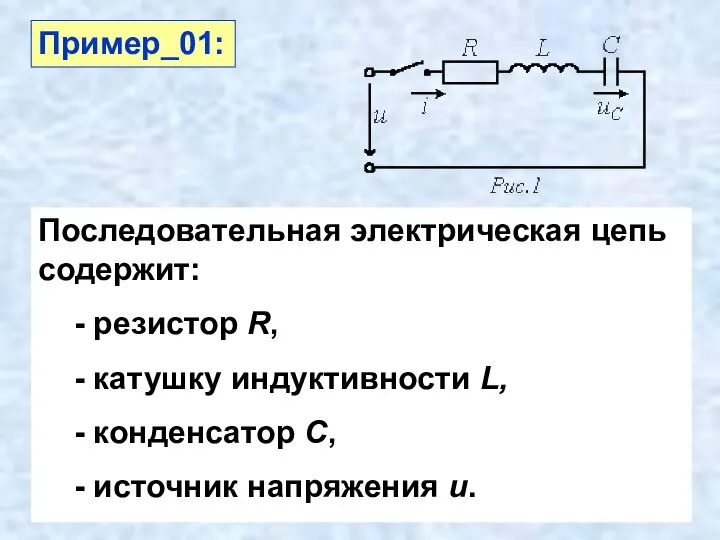
- 24. Последовательная электрическая цепь содержит: - резистор R, - катушку индуктивности L, - конденсатор С, - источник
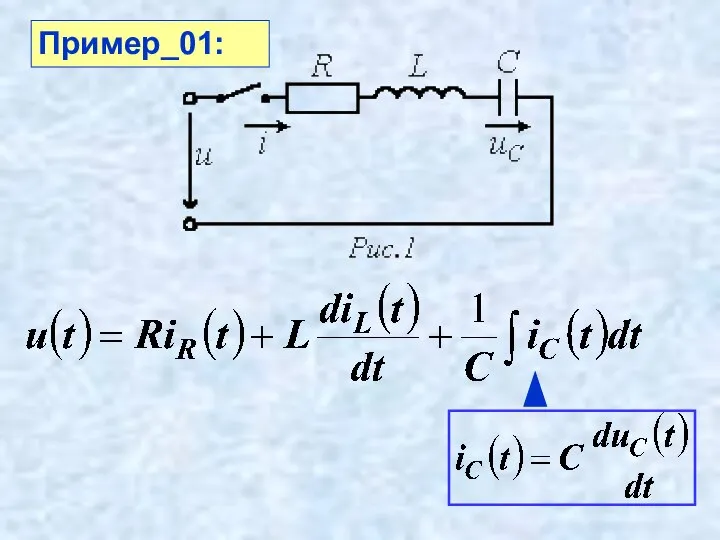
- 25. Пример_01:
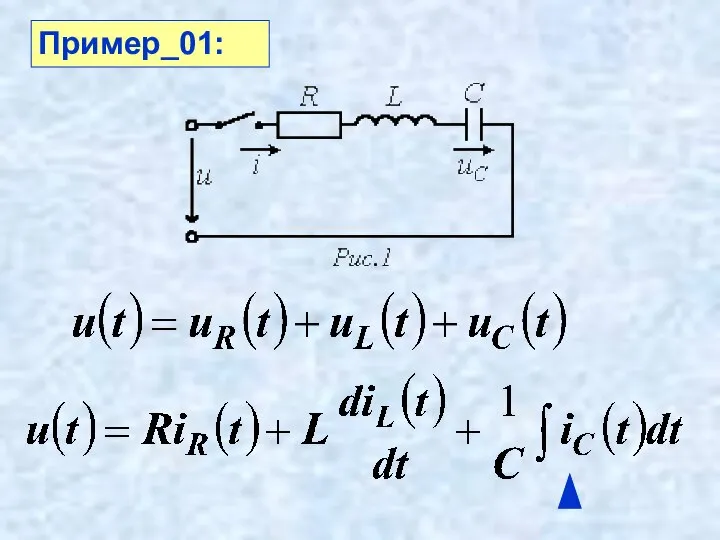
- 26. Пример_01:
- 27. …в итоге получаем линейное дифференциальное уравнение второго порядка относительно uC (t): Пример_01:
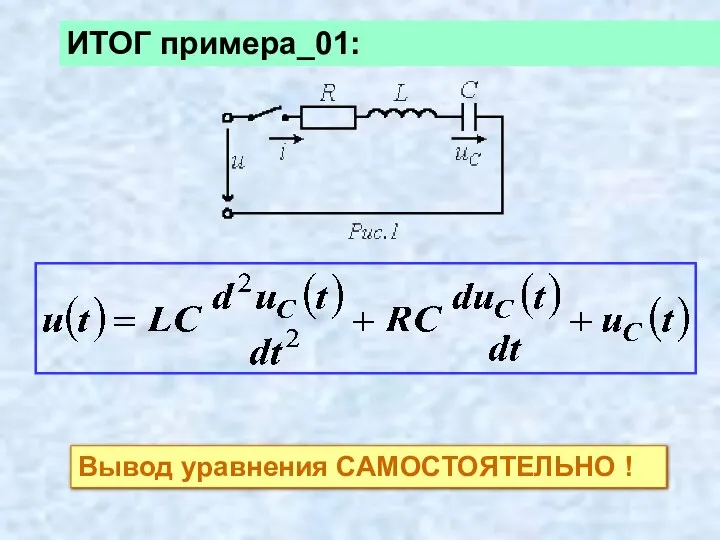
- 28. ИТОГ примера_01: Вывод уравнения САМОСТОЯТЕЛЬНО !
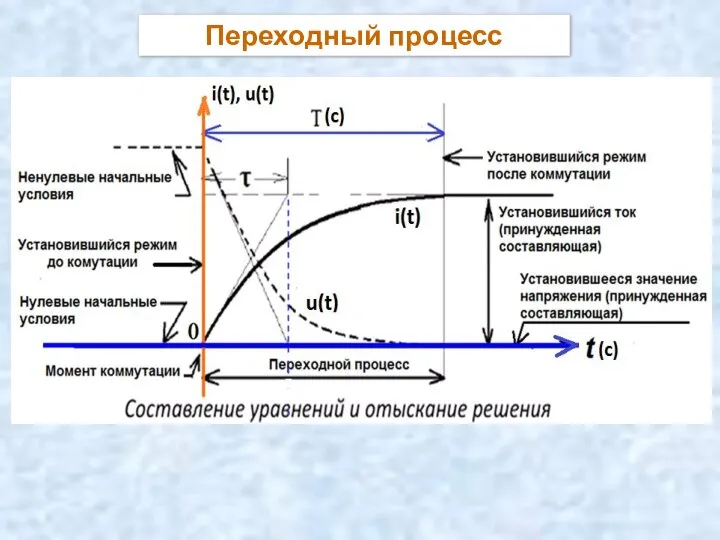
- 29. Переходный процесс
- 30. Методы расчета переходных процессов 1. Классический метод 1.1. Составляется система дифференциальных уравнений эл. цепи с использованием
- 31. 1. Классический метод 1.2. Полученную систему уравнений, путем замены переменных, сводят к дифференциальному уравнению n-го порядка
- 32. 1. Классический метод 1.3. Общее решение полученного линейного дифференциального уравнения ищут в виде суммы двух выражений:
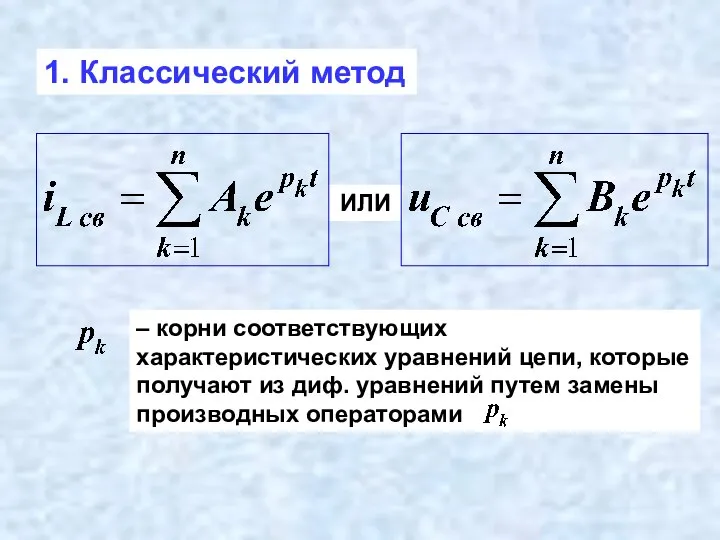
- 33. 1. Классический метод ИЛИ – соответствуют общим решениям, без независимых источников энергии. – соответствуют частным решениям
- 34. 1. Классический метод ИЛИ
- 35. 1. Классический метод ИЛИ – корни соответствующих характеристических уравнений цепи, которые получают из диф. уравнений путем
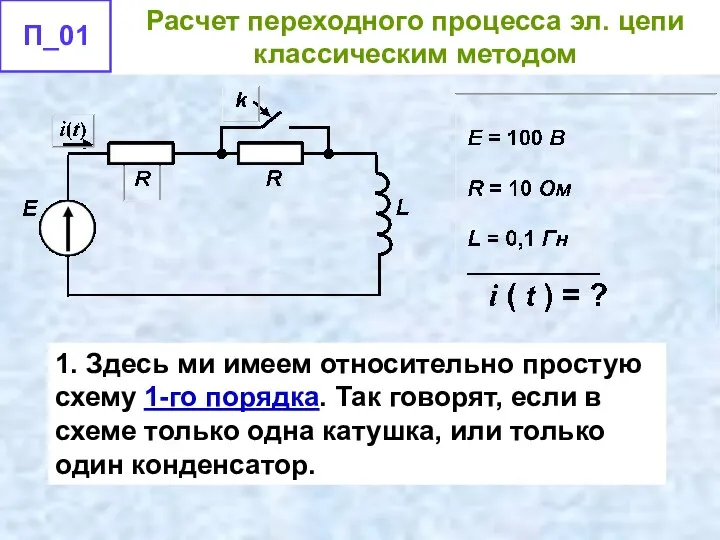
- 38. 1. Здесь ми имеем относительно простую схему 1-го порядка. Так говорят, если в схеме только одна
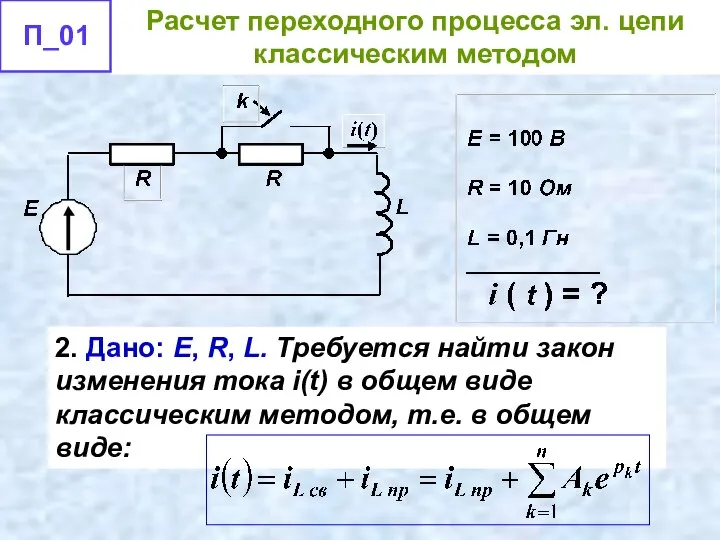
- 39. 2. Дано: E, R, L. Требуется найти закон изменения тока i(t) в общем виде классическим методом,
- 40. 2. Дано: E, R, L. Требуется найти закон изменения тока i(t) в общем виде классическим методом,
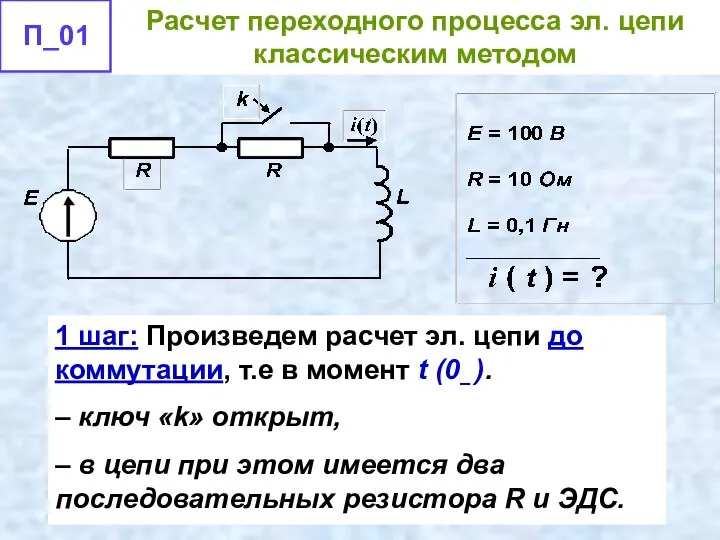
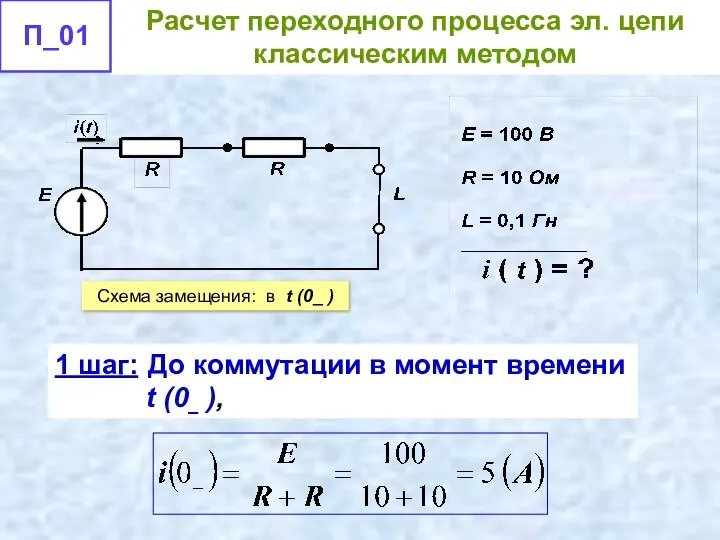
- 41. 1 шаг: Произведем расчет эл. цепи до коммутации, т.е в момент t (0– ). – ключ
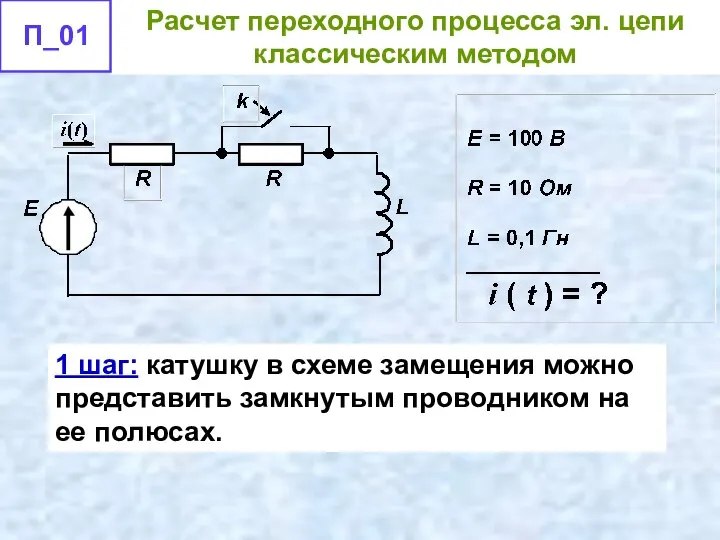
- 42. 1 шаг: катушку в схеме замещения можно представить замкнутым проводником на ее полюсах.
- 43. 1 шаг: До коммутации в момент времени t (0– ), Схема замещения: в t (0_ )
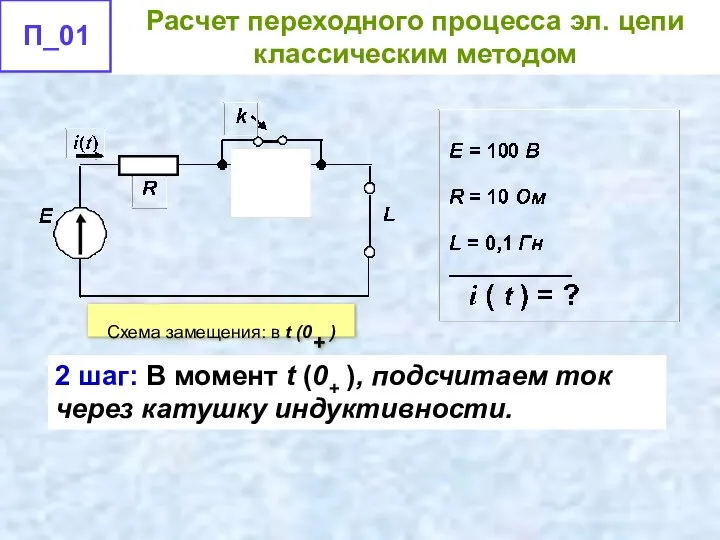
- 44. 2 шаг: В момент t (0+ ), подсчитаем ток через катушку индуктивности. Схема замещения: в t
- 45. В соответствии с классическим методом расчета, ПЕРЕХОДНОЙ ток в ветви схемы представляют в виде суммы ПРИНУЖДЕННОГО
- 46. принужденный ток, определяется в установившемся режиме после коммутации. Этот ток создается внешними источниками питания.
- 47. свободный ток, определяется в схеме после коммутации, из которой исключен внешний источник питания. Свободный ток создается
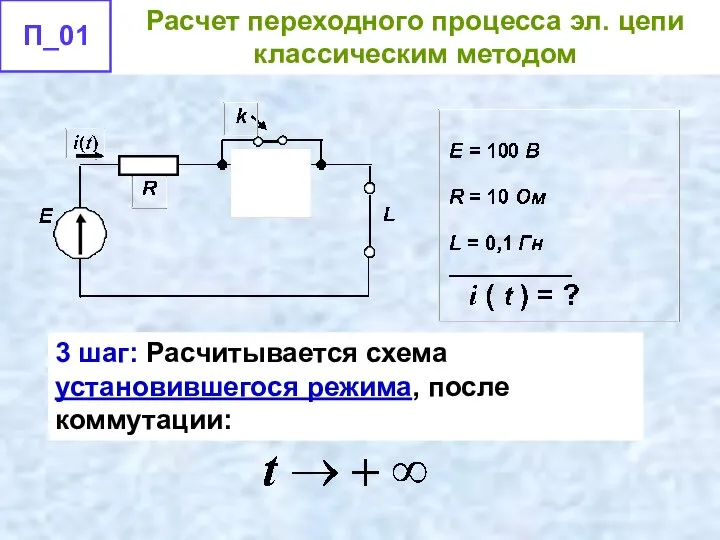
- 48. 3 шаг: Расчитывается схема установившегося режима, после коммутации:
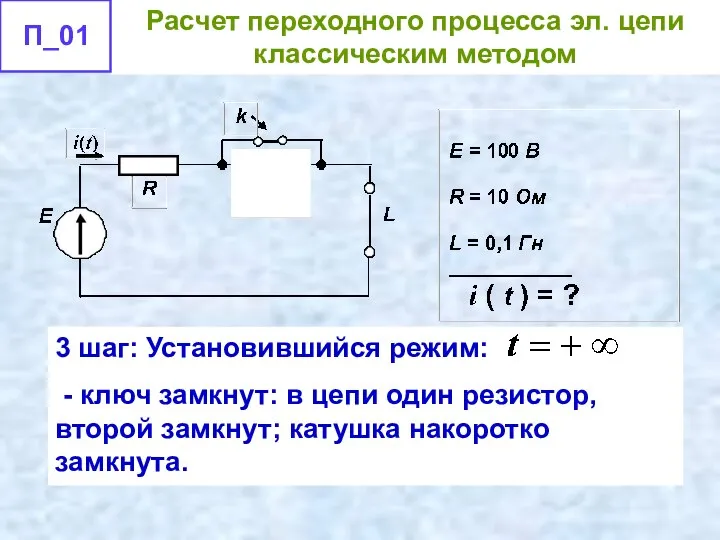
- 49. 3 шаг: Установившийся режим: - ключ замкнут: в цепи один резистор, второй замкнут; катушка накоротко замкнута.
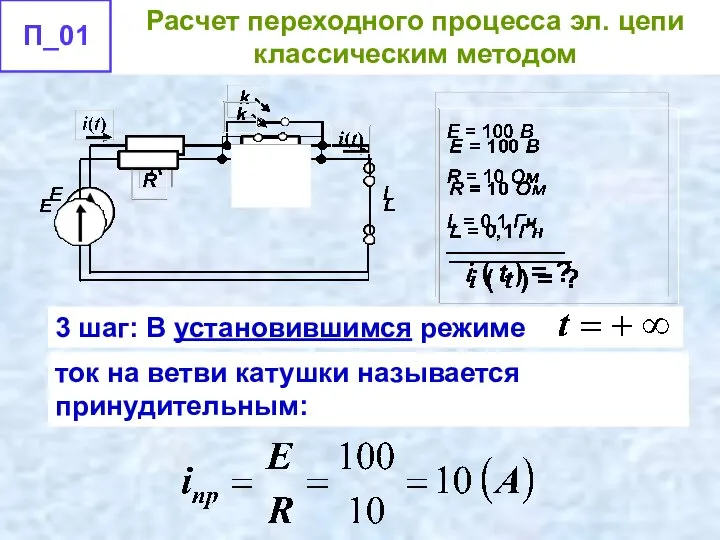
- 50. 3 шаг: В установившимся режиме ток на ветви катушки называется принудительным:
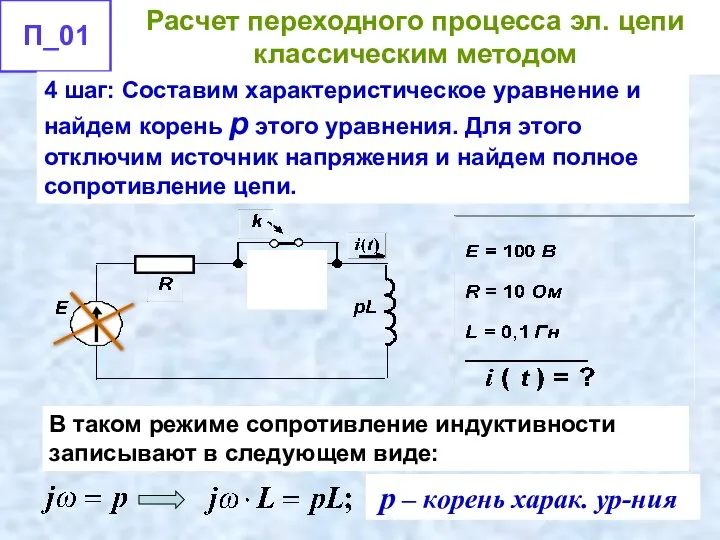
- 51. 4 шаг: Составим характеристическое уравнение и найдем корень p этого уравнения. Для этого отключим источник напряжения
- 52. где p – корень характеристического уравнения Тогда полное сопротивление цепи:
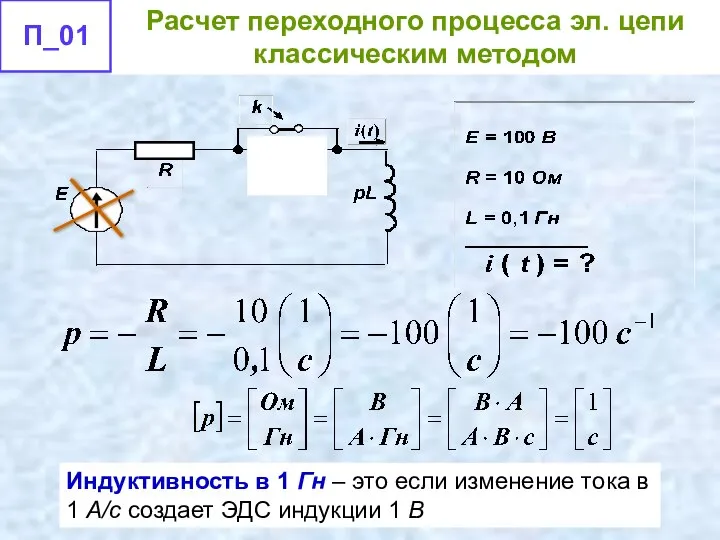
- 53. Индуктивность в 1 Гн – это если изменение тока в 1 А/с создает ЭДС индукции 1
- 54. 5 шаг: Запишем выражение для свободной составляющей тока: Здесь А – постоянная интегрирования
- 55. Найдем постоянную интегрирования А в момент времени t (0+) Выражение для полного решения ищут в виде:
- 56. Выражение для полного решения ищут в виде: Найдем постоянную интегрирования А в момент времени t (0+)
- 57. Выражение для полного решения ищут в виде: В окончательном виде, решения для тока, как функции времени,
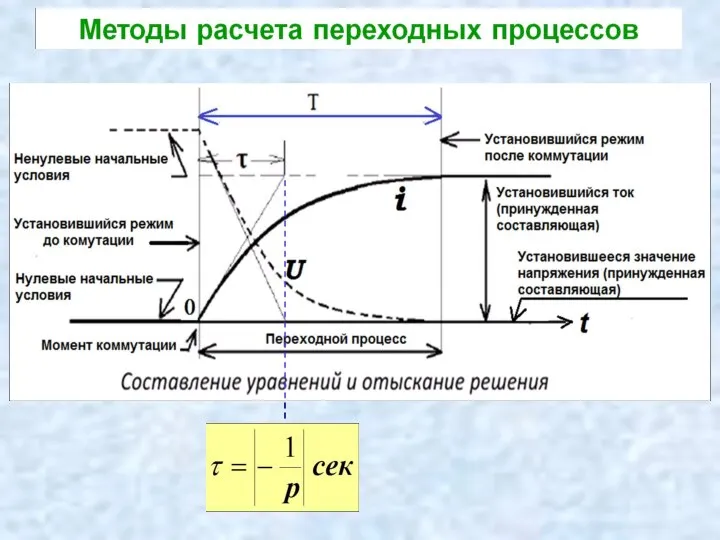
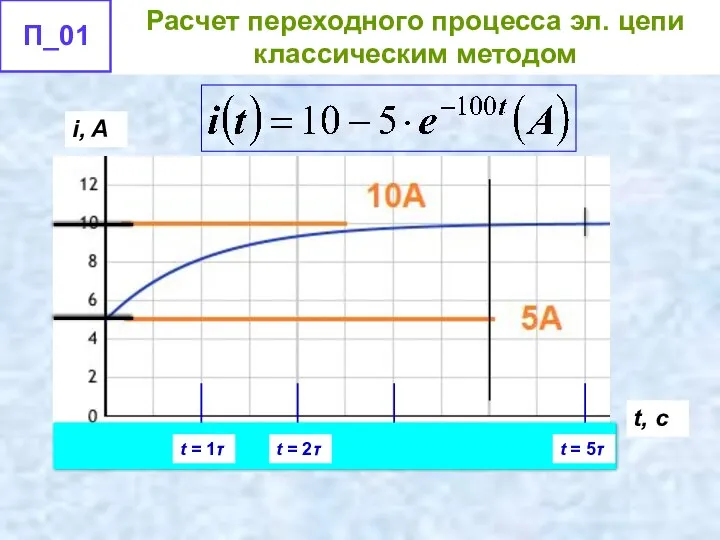
- 59. Построим график зависимости тока от времени: – до коммутвции в момент t (0– ) ток равнялся
- 60. t, c i, A t = 1τ t = 2τ t = 5τ
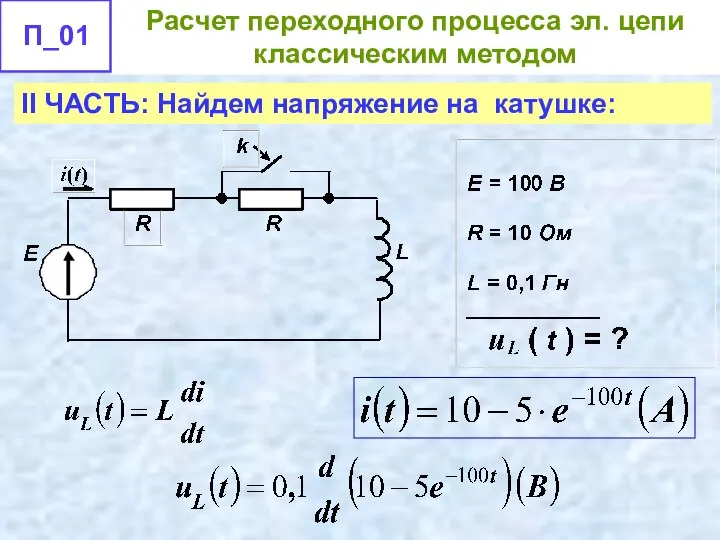
- 61. II ЧАСТЬ: Найдем напряжение на катушке:
- 62. II ЧАСТЬ: Найдем напряжение на катушке:
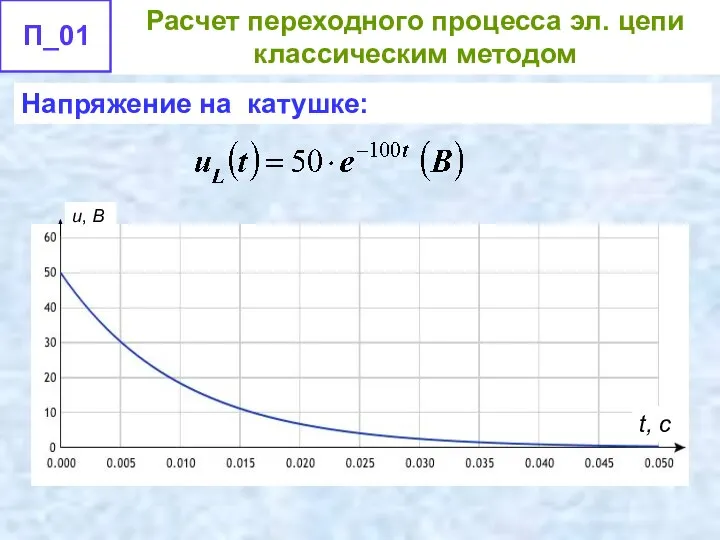
- 63. Напряжение на катушке:
- 65. Скачать презентацию







































 Расчёт кругового поворота автомобиля
Расчёт кругового поворота автомобиля История развития радио. Радиоквиз
История развития радио. Радиоквиз Ядерные силы. Энергия связи частиц в ядре. Деление ядер урана. Цепная реакция
Ядерные силы. Энергия связи частиц в ядре. Деление ядер урана. Цепная реакция Светодиоды. Применение светодиодов
Светодиоды. Применение светодиодов Дисперсия, интерференция, дифракция света
Дисперсия, интерференция, дифракция света Одномерное движение несжимаемой жидкости в условиях водонапорного режима
Одномерное движение несжимаемой жидкости в условиях водонапорного режима Сравнение основных параметров импульсных и линейных источников питания
Сравнение основных параметров импульсных и линейных источников питания Давление тел
Давление тел Double - beta decay of 96zr and double - electron capture of 156dy to excited final states
Double - beta decay of 96zr and double - electron capture of 156dy to excited final states Электропривод. Проектирование электроприводов
Электропривод. Проектирование электроприводов Магнитотерапия. Физическая характеристика
Магнитотерапия. Физическая характеристика Потенциальная энергия. Потенциал однородного поля. Разность потенциалов. Конденсаторы
Потенциальная энергия. Потенциал однородного поля. Разность потенциалов. Конденсаторы Физика космоса, кружок. Космология в ОТО
Физика космоса, кружок. Космология в ОТО Презентация на тему Звуковые колебания и волны
Презентация на тему Звуковые колебания и волны  Электрическое сопротивление. Закон Ома для участка цепи
Электрическое сопротивление. Закон Ома для участка цепи Физика твердого тела
Физика твердого тела Парабола и ее применение в жизни
Парабола и ее применение в жизни Теплообмен при поперечном обтекании труб и пучков
Теплообмен при поперечном обтекании труб и пучков Критерии оценки подвески
Критерии оценки подвески Диэлектрики и проводники в электрическом поле
Диэлектрики и проводники в электрическом поле ООО «ФЛЭР ИНЖИНИРИНГ» Профессиональное сварочное оборудование
ООО «ФЛЭР ИНЖИНИРИНГ» Профессиональное сварочное оборудование Отражение и преломление. Световые явления
Отражение и преломление. Световые явления Физические приборы вокруг нас
Физические приборы вокруг нас Рух тіла під дією кількох сил
Рух тіла під дією кількох сил Визуализация 3М сцен
Визуализация 3М сцен Модификатор зеркало и создание разрезов
Модификатор зеркало и создание разрезов Тепловые двигатели
Тепловые двигатели Презентация на тему Тепловые двигатели
Презентация на тему Тепловые двигатели