Слайд 2Естественный способ задания движения.
При естественном способе задания движения точки уравнение движения выражается

уравнением:
где S – путь точки по ее траектории.
Величина, характеризующая в каждый данный момент времени направление и быстроту движения точки, называется скоростью.
Слайд 3Вектор скорости всегда направлен вдоль касательной в ту сторону, куда движется точка
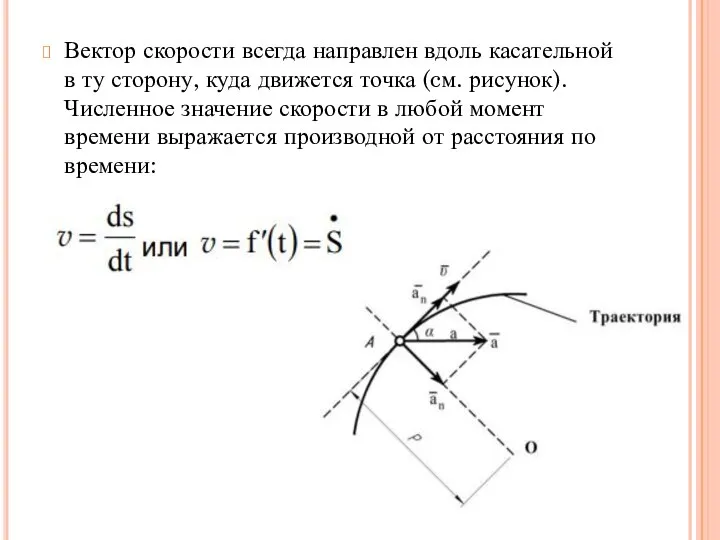
(cм. рисунок). Численное значение скорости в любой момент времени выражается производной от расстояния по времени:
Слайд 4Ускорение (а) точки в каждый данный момент времени характеризует быстроту изменения скорости.

При этом нужно помнить, что скорость — вектор, и, следовательно, изменение скорости может происходить по двум признакам: по числовой величине (по модулю) и по направлению.
Быстрота изменения модуля скорости характеризуется касательным ускорением — составляющей полного ускорения направленной по касательной к траектории как показано на рисунке
Численное значение касательного ускорения в общем случае определяется по формуле:
Слайд 5Направление касательного ускорения совпадает с направлением скорости, если они имеют одинаковые знаки.

Касательное ускорение направлено в сторону, противоположную направлению скорости в случае, когда знаки их разные.
Быстрота изменения направления скорости характеризуется нормальным ускорением составляющей полного ускорения , направленной по нормали к траектории в сторону центра кривизны
Слайд 6Численное значение нормального ускорения определяется в общем случае по формуле:
где v модуль

скорости точки в данный момент; ρ — радиус кривизны траектории в месте, где находится точка в данный момент времени. После того как определены касательное и нормальное ускорения, легко определить полное ускорение точки. Так как касательная и нормаль взаимно перпендикулярны, то численное значение полного ускорения a можно определить по теореме Пифагора:
Слайд 7Величину полного ускорения можно найти по формуле:
Касательное и нормальное ускорения точки являются

главными кинематическими величинами, определяющими вид и особенности движения точки.
Наличие касательного ускорения ( ≠ 0) или его отсутствие ( = 0) определяют, соответственно, неравномерность или равномерность движения точки.






 Механические явления
Механические явления Механические колебания и волны
Механические колебания и волны Баллистическое движение
Баллистическое движение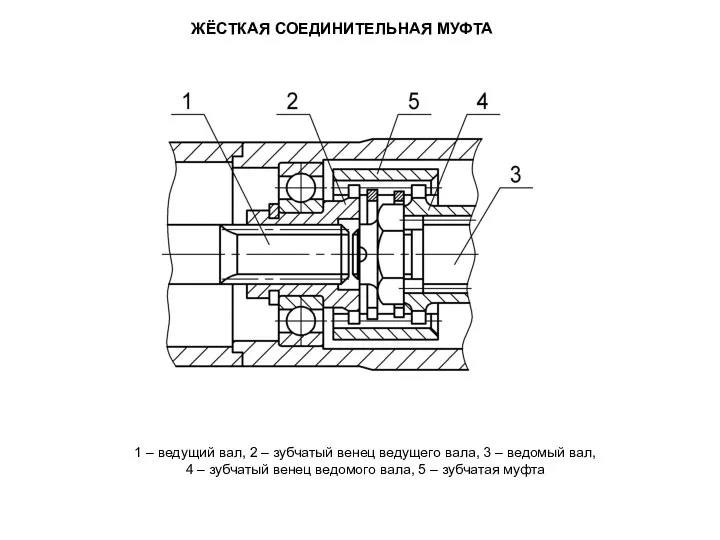 Шарнирные передачи
Шарнирные передачи Найкрутiша презентацiя
Найкрутiша презентацiя Силы в природе
Силы в природе Презентация на тему Ускорение
Презентация на тему Ускорение  Пневматика
Пневматика Электрическая цепь и её составные части
Электрическая цепь и её составные части Школа юного исследователя
Школа юного исследователя Сила тока. Измерение силы тока
Сила тока. Измерение силы тока Элементы трехфазных цепей
Элементы трехфазных цепей Измерение мощности в трехфазной цепи
Измерение мощности в трехфазной цепи Презентация на тему Ускоренное движение свободного падения
Презентация на тему Ускоренное движение свободного падения  Застосування комп’ютерних технологій у спектрофотометрії
Застосування комп’ютерних технологій у спектрофотометрії Второй закон Ньютона
Второй закон Ньютона Переменный электрический ток
Переменный электрический ток Презентация на тему Электростатика
Презентация на тему Электростатика  Prüfen und Einstellen
Prüfen und Einstellen Оценка прочности плоской фермы при нагреве
Оценка прочности плоской фермы при нагреве Метод наложения для расчета электрических цепей
Метод наложения для расчета электрических цепей Электроэнергия. Гидроэлектростанция. Линия электропередач. Электролампа
Электроэнергия. Гидроэлектростанция. Линия электропередач. Электролампа Температура. Виды термометров
Температура. Виды термометров Проводники и диэлектрики
Проводники и диэлектрики Формула Планка
Формула Планка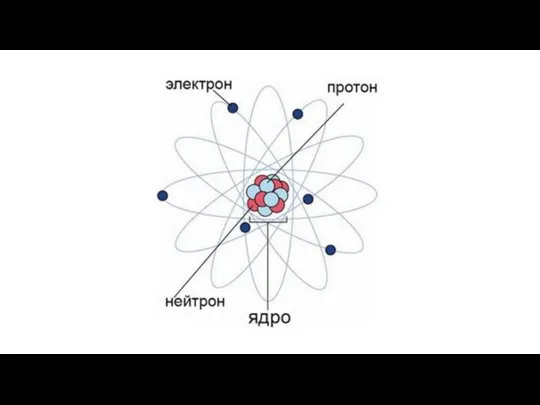 Строение атома
Строение атома Тонкослойная хроматография
Тонкослойная хроматография Основы термодинамики
Основы термодинамики