Содержание
- 2. Допуск Поле допуска Основное отклонение Отверстие и вал Посадки Допуск (обычно обозначается буквой "Т") – разность
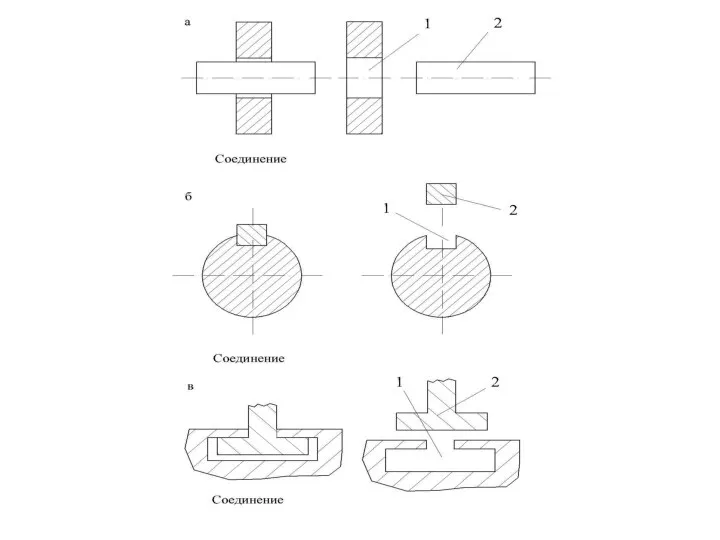
- 4. Рисунок 2 – Отверстия и валы:а, б, в – виды соединений элементов деталей; 1 – отверстие,
- 5. Тогда ES = Dмакс – Dн; EI = Dмин – Dн; es = dмакс – dн;
- 6. СИСТЕМА ДОПУСКОВ И ПОСАДОК ДЛЯ ЭЛЕМЕНТОВ ДЕТАЛЕЙ С ГЛАДКОЙ ПОВЕРХНОСТЬЮ Таким образом, при изготовлении деталей возникают
- 7. Отверстие и вал Верхнее отклонение ES, es - алгебраическая разность между наибольшим и номинальным размерами. ES
- 8. Посадка – характер соединения двух деталей, определяемый разностью их размеров до сборки. Допуск посадки – Сумма
- 9. Единая система допусков и посадок (ЕСДП) Системой допусков и посадок называется закономерно построенная совокупность стандартизованных допусков
- 10. Выбор размеров, ряды предпочтительных чисел Номинальные линейные размеры (диаметры, длины, уступы, глубины, расстояния между осями и
- 11. Исходя из особенностей взаимосвязи размера детали и возможности в отношении точности изготовления, установленные в системах допусков
- 12. Для некоторых квалитетов (0,1; 0; 1) допуски определяются по специальным формулам. В табл. 2.2 приведено количество
- 13. Второй принцип построения СДП (установлено 27 основных отклонений валов и 27 основных отклонений отверстий) Основные отклонения
- 14. El = -es; ES = -ei.
- 15. Третий принцип построения СДП (Предусмотрены системы образования посадок) Система отверстия и вала В системе отверстия различные
- 16. Сущность этих систем заключается в том, что при образовании всех трех видов посадок вводится ограничение на
- 19. Система вала применяется в следующих случаях: 1. Когда на вал одного диаметра требуется установить несколько деталей
- 20. Четвертый принцип построения СДП (установлена нормальная температура.) +200С Правила образования посадок 1. Посадки с 4-го по
- 21. Посадки в ЕСДП и их обозначение на чертежах В системе отверстия различные посадки образуются сочетанием всего
- 22. Обозначение посадок на чертежах деталей
- 24. Здесь G - основное отклонение для отверстия: 7 - квалитет для отверстия; h - основной вал
- 25. Посадки Посадка - характер соединения деталей, определяемый значениями получающихся в нем зазоров или натягов. Зазор -
- 26. . Dн = 105 мм. ES = 0,035 мм. EI = 0. dн = 105 мм.
- 27. Посадки с натягом Посадка с натягом - это посадка, при которой всегда образуется натяг в соединении,
- 28. Переходные посадки В этих посадках может образовываться как зазор, так и натяг. Переходная посадка - посадка,
- 29. В практической деятельности используются предпочтительные поля допусков. Это в значительной мере способствует экономической эффективности производства, поскольку
- 30. Практические рекомендации по выбору посадок Валы 4-5 квалитетов и отверстия 5-6 квалитетов получаются, в основном, круглым
- 31. Рекомендуемые посадки для использования в соединениях приведены в табл. 2.4.
- 32. Калибры. Требования к точности и контроль деталей калибрами Годность деталей с допуском от IT6 до IT17,
- 33. НОРМИРОВАНИЕ ТОЧНОСТИ ФОРМЫ И РАСПОЛОЖЕНИЯ ПОВЕРХНОСТЕЙ ДЕТАЛЕЙ Отклонение формы поверхностей Отклонением формы называется отклонение реальной поверхности
- 34. Отсчет этого отклонения производится от точек реального профиля до прилегающей прямой. Прилегающей называется прямая, которая касается
- 36. Прилегающим цилиндром называется цилиндр минимального диаметра, описанный вокруг реальной наружной поверхности или максимального диаметра, вписанный в
- 39. Таким образом, отклонение от прямолинейности в плоскости - это наибольшее расстояние Δ (E) от точек реального
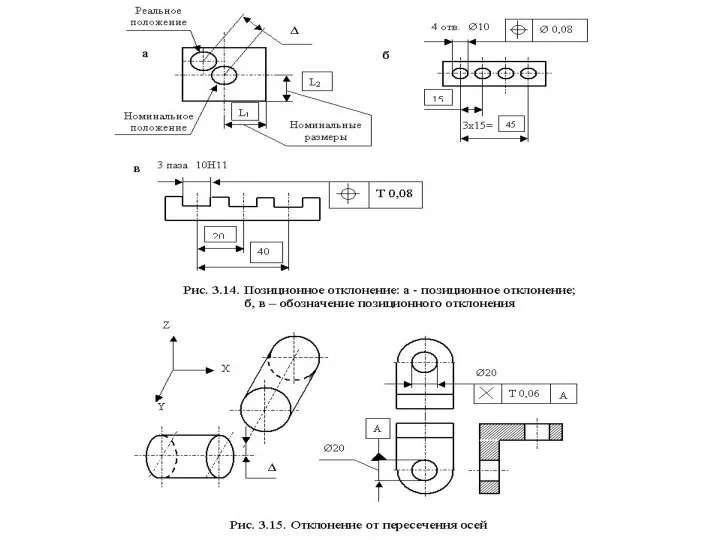
- 40. Отклонения расположения поверхностей Отклонение расположения поверхности или профиля детали - это отклонение их реального положения от
- 49. Суммарные отклонения формы и расположения поверхностей Допускается использовать любые сочетания отклонений формы и расположения, если между
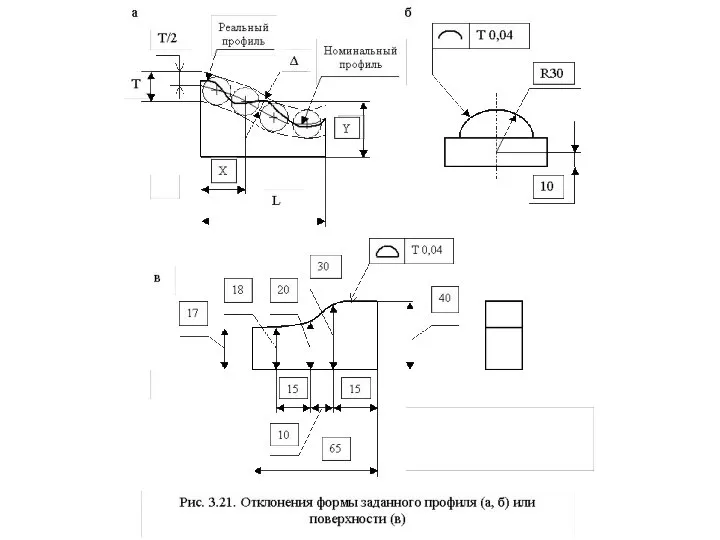
- 52. Отклонение формы заданного профиля или поверхности - это наибольшее отклонение точек реального профиля или поверхности от
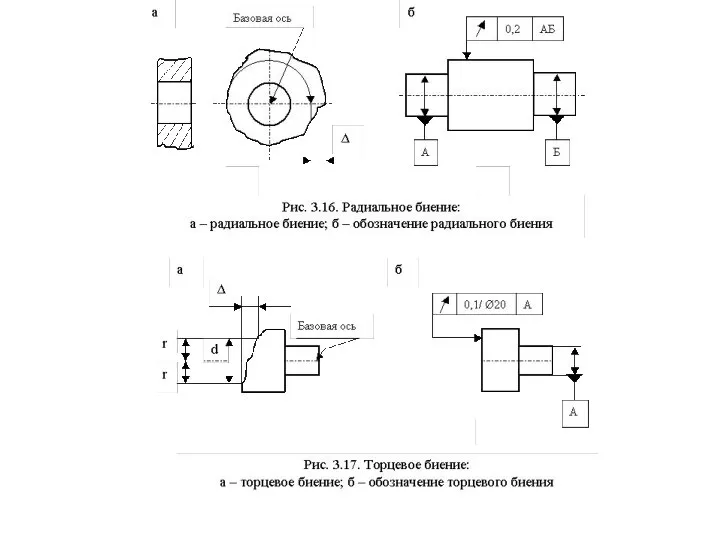
- 54. Радиальное биение - это разность наибольшего и наименьшего расстояний от точек реального профиля поверхности до базовой
- 55. Зависимые отклонения и допуски формы и расположения поверхностей Отклонения формы и расположения поверхностей могут зависеть от
- 56. Итак, зависимое отклонение (допуск) формы и расположения поверхностей - это отклонение (допуск), зависящее от действительных размеров
- 58. Числовые значения отклонений (допусков) формы и расположения поверхностей Согласно ГОСТ 24643 (Основные нормы взаимозаменяемости. Допуски расположения.
- 59. НОРМИРОВАНИЕ ТРЕБОВАНИЙ К НЕРОВНОСТЯМ НА ПОВЕРХНОСТИ ЭЛЕМЕНТОВ ДЕТАЛЕЙ (ШЕРОХОВАТОСТЬ ПОВЕРХНОСТИ) Шероховатостью поверхности называется совокупность неровностей поверхности
- 60. Высота неровностей по десяти точкам Высота неровностей по десяти точкам Rz - это сумма средних абсолютных
- 61. Указание требований к поверхностным неровностям, одинаковым для нескольких элементов детали Расположение знаков на чертеже детали с
- 62. Таблица 4.1 Соотношение между параметрами шероховатости
- 63. НОРМИРОВАНИЕ ТОЧНОСТИ ДЕТАЛЕЙ, СОПРЯГАЕМЫХ С ПОДШИПНИКАМИ КАЧЕНИЯ Подшипник - это деталь или узел механизма, являющийся опорой
- 64. Класс точности подшипника характеризуется целым комплексом точностных требований, относящихся к отклонениям размеров, формы и расположения: 1.
- 65. 1. Требования к точности присоединительных размеров D, d, В, отклонений формы и расположения поверхностей колец и
- 66. Посадки подшипников качения Поля допусков колец подшипников качения Классы точности подшипников качения характеризуются допуском на размер.
- 67. Поскольку кольца подшипника являются податливым звеном, то при их установке часто используются или переходные посадки, или
- 68. Поля допусков для размеров посадочных поверхностей валов и отверстий корпусов под подшипники качения Таблица 5.1 Поля
- 69. Таблица 5.2 Поля допусков отверстий для основных видов сопряжений посадочных поверхностей по наружному кольцу подшипника
- 70. Посадки подшипников качения на валы и отверстия корпусов Посадки по наружному диаметру подшипника осуществляются в системе
- 71. Технические требования к посадочным поверхностям валов и корпусов под подшипники качения
- 72. Выбор посадок для колец подшипников Рекомендации при выборе посадок подшипников Нельзя устанавливать с большим натягом наружное
- 73. Кольца подшипника во время работы могут испытывать различные виды нагружений. Бывают следующие виды нагружений: местное, циркуляционное
- 75. НОРМИРОВАНИЕ ТОЧНОСТИ ШПОНОЧНЫХ СОЕДИНЕНИЙ Шпоночное соединение вала с установленным на нем отверстием с по-мощью шпонки, т.е.
- 76. Глубина пазов под шпонку у валов t1 - от 1,2 до 31 мм, у втулок t2
- 77. Плотное соединение - соединение с переходной посадкой с приблизительно равной вероятностью зазоров и натягов. В этих
- 78. Иногда шпоночные соединения разделяют на затяжные, когда шпонка устанавливается с затяжкой вдоль оси, т.е. с натягом
- 79. НОРМИРОВАНИЕ ТОЧНОСТИ ЦИЛИНДРИЧЕСКИХ ЗУБЧАТЫХ КОЛЕС И ПЕРЕДАЧ Зубчатое колесо представляет собой деталь сложной геометрической формы в
- 80. Ряды точности (допуски) для зубчатых колес и передач по параметрам зацепления При нормировании точности зубчатых колес
- 81. Схема расположения полей допусков Tjn для принятых видов сопряжений зубьев зубчатых колес Так как на значение
- 82. Условные обозначения требований к точности зубчатых колес и передач Таблица 11.1. Чертежи колес выполняются в соответствии
- 83. Нормируемые параметры (показатели), характеризующие точность зубчатых колес и передач Показатель кинематической точности Кинематической погрешностью передачи (F'ior)
- 84. Таблица 11.2. Показатели кинематической точности (основные)
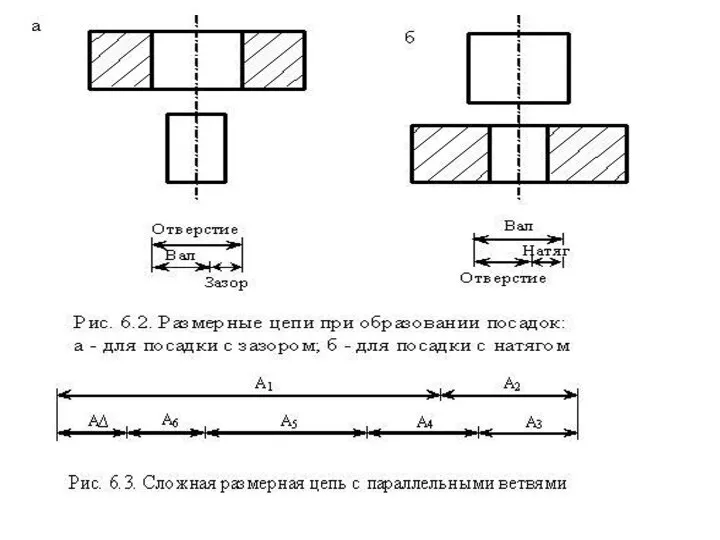
- 86. ОБЕСПЕЧЕНИЕ ТОЧНОСТИ РАЗМЕРНЫХ ЦЕПЕЙ Взаимосвязь размеров элементов детали или отдельных деталей, входящих в конструкцию сборочной единицы
- 88. Увеличивающим звеном размерной цепи называется звено, с увеличением которого размер замыкающего звена тоже увеличивается. На рис.6.3
- 89. Виды размерных цепей Задачи, решаемые при обеспечении точности размерных цепей Задача 1. Определение предельных размеров замыкающего
- 90. Задача 2. Определение предельных размеров составляющих звеньев размерной цепи, когда известны предельные размеры замыкающего звена и
- 91. Номинальный размер замыкающего звена равен сумме номинальных размеров увеличивающих звеньев (ΣАув) минус сумма размеров уменьшающих звеньев
- 92. Допуск замыкающего звена равен сумме допусков составляющих звеньев. Отсюда следует, что допуск любого звена может быть
- 93. Пример. Определить номинальное, наибольшее и наименьшее значения и допуск замыкающего звена (размера АΔ) - рис.6.6. Составляем
- 94. Определяем номинальное значение АΔ по формуле АΔ = (А1 + A2) - (А3 + А4 +
- 95. Пример. Определить допуски составляющих размеров деталей сборочной единицы, показанной на рис.6.6. Схема размерной цепи показана на
- 97. Скачать презентацию
Слайд 2Допуск Поле допуска Основное отклонение Отверстие и вал Посадки
Допуск (обычно обозначается буквой
Допуск Поле допуска Основное отклонение Отверстие и вал Посадки
Допуск (обычно обозначается буквой

Поле допуска - поле (заштрихованный прямоугольник на рис. 3.1, в), ограниченное наибольшим и наименьшим предельными размерами, определяемое значением допуска и его положением относительно номинального размера.
Основное отклонение – одно из двух отклонений (верхнее или нижнее), используемое для определения положения поля допуска относительно нулевой линии. Основным отклонением является отклонение, ближайшее к нулевой линии. У полей допусков, расположенных над нулевой линией, основными отклонениями являются нижние отклонения, а у расположенных под нулевой линией - верхние отклонения.
Вал – термин, условно применяемый для обозначения наружных элементов деталей (элемент с наружной охватываемой поверхностью), включая и нецилиндрические элементы.
Отверстие – термин, условно применяемый для обозначения внутренних элементов деталей (элемент с внутренней охватывающей поверхностью), включая и нецилиндрические.
Слайд 4Рисунок 2 – Отверстия и валы:а, б, в – виды соединений элементов
Рисунок 2 – Отверстия и валы:а, б, в – виды соединений элементов
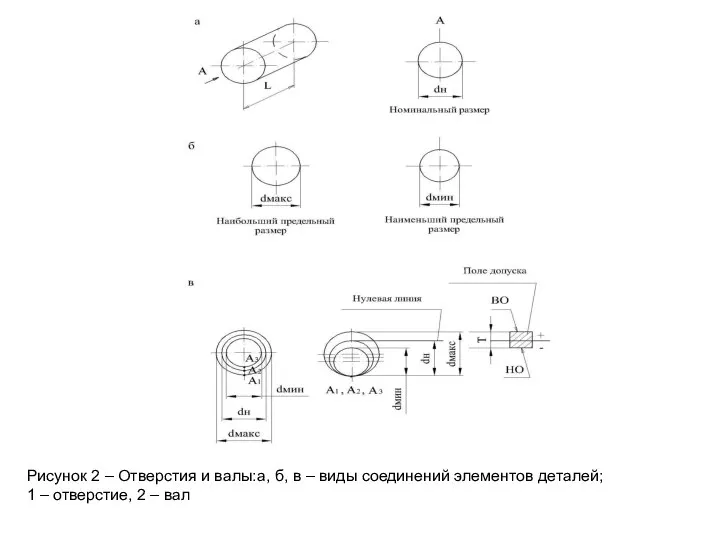
1 – отверстие, 2 – вал
Слайд 5 Тогда ES = Dмакс – Dн; EI = Dмин – Dн; es
Тогда ES = Dмакс – Dн; EI = Dмин – Dн; es

Разность между наибольшими и наименьшими предельными размерами, а следовательно, между верхним предельным и нижним предельным отклонениями называется допуском размера. Допуск размера обозначается ТD для отверстия и Td для вала. Таким образом
ТD = Dмакс – Dмин = ES – EI; Td = dмакс – dмин = es – ei.
Из приведенных формул следует, что допуск – величина всегда положительная, в то время как предельные отклонения, как уже было отмечено ранее, величины алгебраические, т.е. могут иметь знак “+” или “–“.
В результате соединения отверстия с валом образуется посадка. Посадкой определяется плотность соединения деталей.
Посадка – характер соединения деталей, определяемый значениями получающихся в нем зазоров или натягов.
Зазор – разность между размерами отверстия и вала до сборки, если размер отверстия больше размера вала (обозначается S).
Натяг – разность размеров вала и отверстия до сборки, если размер вала больше размера отверстия (обозначается N).
Добавление в определениях слов "до сборки" объясняется тем, что в результате сборки может происходить деформация сопрягаемых поверхностей (при натяге).
В зависимости от свободы относительного перемещения сопрягаемых деталей или степени сопротивления взаимному смещению посадки разделяются на три вида:
- посадки с зазором;
- посадки с натягом;
- переходные посадки.
Слайд 6СИСТЕМА ДОПУСКОВ И ПОСАДОК ДЛЯ ЭЛЕМЕНТОВ ДЕТАЛЕЙ С ГЛАДКОЙ ПОВЕРХНОСТЬЮ
Таким образом,
СИСТЕМА ДОПУСКОВ И ПОСАДОК ДЛЯ ЭЛЕМЕНТОВ ДЕТАЛЕЙ С ГЛАДКОЙ ПОВЕРХНОСТЬЮ
Таким образом,
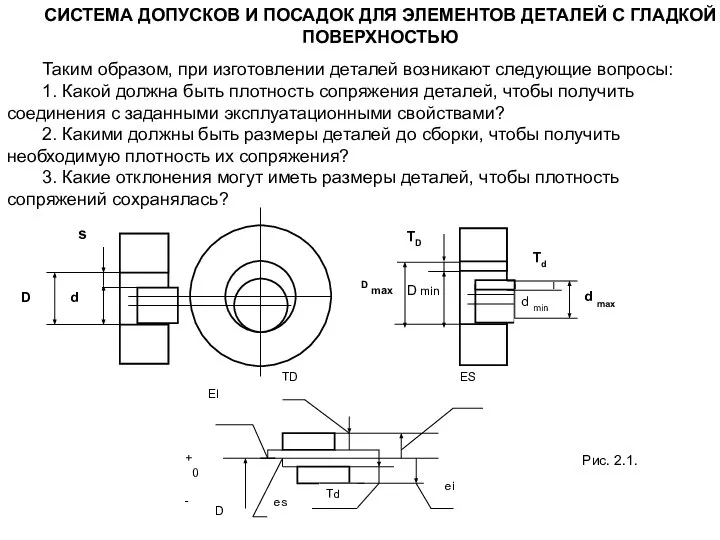
1. Какой должна быть плотность сопряжения деталей, чтобы получить соединения с заданными эксплуатационными свойствами?
2. Какими должны быть размеры деталей до сборки, чтобы получить необходимую плотность их сопряжения?
3. Какие отклонения могут иметь размеры деталей, чтобы плотность сопряжений сохранялась?
Рис. 2.1.
Слайд 7Отверстие и вал
Верхнее отклонение ES, es - алгебраическая разность между наибольшим и
Отверстие и вал
Верхнее отклонение ES, es - алгебраическая разность между наибольшим и

ES = Dmax – D; es = dmax - D.
Нижнее отклонение EI, ei – алгебраическая разность между наименьшим и номинальным размерами.
EI = Dmin – D; ei = dmin – D.
Поле допуска – поле, ограниченное наибольшим и наименьшим предельными размерами и определяемое величиной допуска и его положением относительно нулевой линии, соответствующей номинальному размеру.
Определение терминов, вошедших в раздел, по ГОСТ 25346-89
Размер – числовое значение линейной величины (диаметр, длина итп) в выбранных единицах измерения.
Действительный размер - размер элемента, установленный измерением с допустимой погрешностью.
Нулевая линия – линия соответствующая номинальному размеру, от которой откладываются отклонения размеров при графическом изображении полей допусков и посадок.
Вал – термин, условно применяемый для обозначения внутренних элементов деталей, включая и нецилиндрические элементы.
Отверстие – термин, условно применяемый для обозначения внутренних элементов деталей, включая и нецелендричкские элементы.
Слайд 8Посадка – характер соединения двух деталей, определяемый разностью их размеров до сборки.
Допуск
Посадка – характер соединения двух деталей, определяемый разностью их размеров до сборки.
Допуск

Зазор – разность между размерами отверстия и вала до сборки, если отверстие больше размера вала.
Натяг – Разность между размерами вала и отверстия , если размер вала больше размера отверстия.
Посадка с зазором – посадка, при которой всегда образуется зазор в соединении, т.е. наименьший предельный размер отверстия больше наименьшего предельного размера вала или равен ему. При графическом изображении поле допуска отверстия всегда выше поля допуска вала.
Посадка с натягом – посадка, при которой всегда образуется натяг в соединении, т.е. наибольший предельный размер отверстия меньше наименьшего предельного размера вала или равен ему. При графическом изображении поле допуска отверстия всегда расположено под полем допуска вала.
Переходная посадка – посадка, при которой возможно получение как зазороа так и натяга в соединении в зависимости от действительных размеров как отверстия так и вала. При графическом изображении поля допусков отверстия и вала перекрываются полностью или частично.
Квалитет – совокупность допусков, рассматриваемых как соответствующие одному уровню точности для всех номинальных размеров.
Слайд 9Единая система допусков и посадок (ЕСДП)
Системой допусков и посадок называется закономерно
Единая система допусков и посадок (ЕСДП)
Системой допусков и посадок называется закономерно

Можно дать еще одно определение системы допусков и посадок как совокупности рядов допусков и посадок, закономерно построенных на основе производственного опыта, экспериментальных исследований, теоретических обобщений и оформленных в виде стандартов.
Первый принцип построения СДП (установлено 20 квалитетов и определены формулы для расчета допусков)
Квалитет (класс, степень точности) - совокупность допусков, соответствующих одному уровню точности для всех номинальных размеров.
В ЕСДП предусмотрено 20 квалитетов, обозначаемых в порядке уменьшения точности (т.е. допуск увеличивается) 0,1; 0; 1; 2; 3 ... 17; 18. Сокращенно допуск по квалитету обозначается буквами IT (первые буквы английских слов International Tolerance - международный допуск) с указанием номера квалитета, например IT8 - означает допуск по 8-му квалитету. Нестандартный допуск (без отнесения к системе) обозначается буквой Т.
Стандартный допуск получают умножением единицы допуска i на постоянное для данного квалитета число k, которое называется числом единиц допуска
IT = ki.
Слайд 10Выбор размеров, ряды предпочтительных чисел
Номинальные линейные размеры (диаметры, длины, уступы, глубины,
Выбор размеров, ряды предпочтительных чисел
Номинальные линейные размеры (диаметры, длины, уступы, глубины,

Стандарт на нормальные линейные размеры построен на основе рядов предпочтительных чисел по ГОСТ 8032, представляющий собой геометрические прогрессии со знаменателем
где R равно 5; 10; 20; 40; 80 и 160.
Значение R указывает на количество чисел, содержащихся в каждом десятичном интервале (например, в интервале от 1 до 10 при R = 5 содержатся следующие пять стандартных чисел: 1,0; 1,6; 2,5; 4,0; 6,3), и входит в обозначение ряда. Эти ряды условно названы R5, R10, R20, R40 - основные ряды - и R80, R160 - дополнительные ряды. Почему выбрана геометрическая прогрессия? Потому что число членов ряда получается меньшим по сравнению с арифметической прогрессией.
Единицы допуска
При назначении допусков необходимо было выбрать закономерность изменения допусков с учетом значения номинального размера. Поэтому в каждой системе имеется так называемая единица допуска (обозначается i), которая является как бы масштабом (мерой) допуска.
Единица допуска зависит от крайних значений интервала номинальных размеров Dн мин и Dн макс. В ЕСДП для размеров от 1 до 500 мм единица допуска определяется по выражениям (для квалитетов≥5):
где D - среднегеометрическое крайних значений интервала номинальных размеров
Слайд 11Исходя из особенностей взаимосвязи размера детали и возможности в отношении точности изготовления,
Исходя из особенностей взаимосвязи размера детали и возможности в отношении точности изготовления,
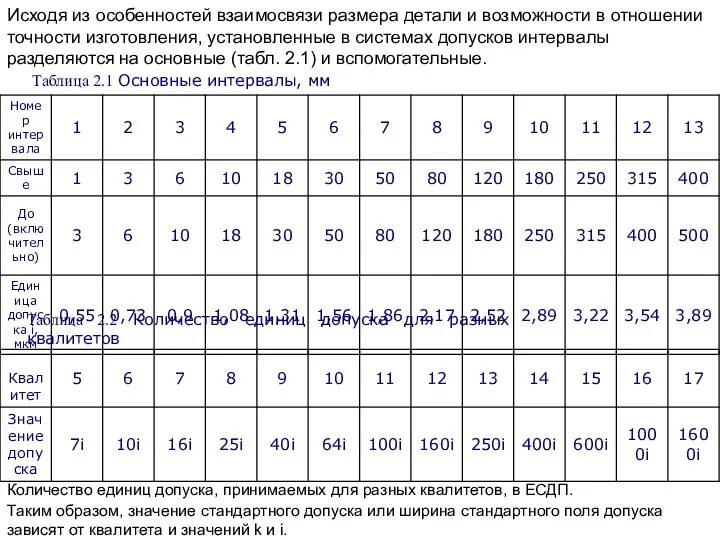
Таблица 2.1 Основные интервалы, мм
Таблица 2.2 Количество единиц допуска для разных квалитетов
Количество единиц допуска, принимаемых для разных квалитетов, в ЕСДП.
Таким образом, значение стандартного допуска или ширина стандартного поля допуска зависят от квалитета и значений k и i.
Слайд 12Для некоторых квалитетов (0,1; 0; 1) допуски определяются по специальным формулам.
В табл.
Для некоторых квалитетов (0,1; 0; 1) допуски определяются по специальным формулам.
В табл.
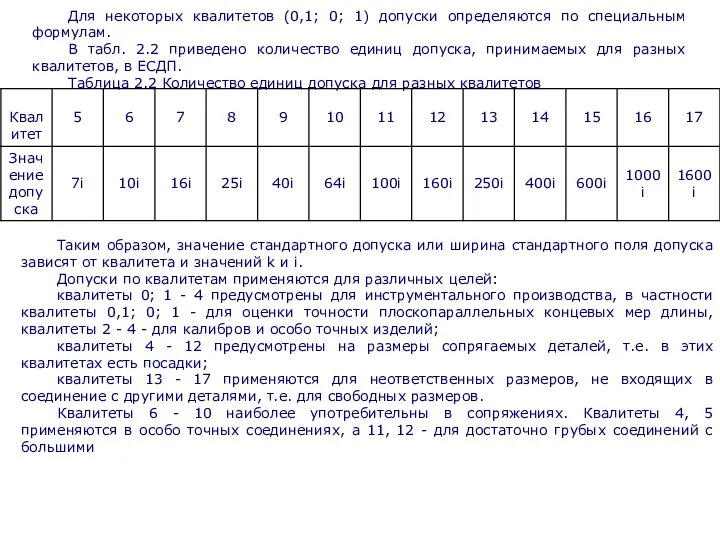
Таблица 2.2 Количество единиц допуска для разных квалитетов
Таким образом, значение стандартного допуска или ширина стандартного поля допуска зависят от квалитета и значений k и i.
Допуски по квалитетам применяются для различных целей:
квалитеты 0; 1 - 4 предусмотрены для инструментального производства, в частности квалитеты 0,1; 0; 1 - для оценки точности плоскопараллельных концевых мер длины, квалитеты 2 - 4 - для калибров и особо точных изделий;
квалитеты 4 - 12 предусмотрены на размеры сопрягаемых деталей, т.е. в этих квалитетах есть посадки;
квалитеты 13 - 17 применяются для неответственных размеров, не входящих в соединение с другими деталями, т.е. для свободных размеров.
Квалитеты 6 - 10 наиболее употребительны в сопряжениях. Квалитеты 4, 5 применяются в особо точных соединениях, а 11, 12 - для достаточно грубых соединений с большими
Слайд 13Второй принцип построения СДП (установлено 27 основных отклонений валов и 27 основных
Второй принцип построения СДП (установлено 27 основных отклонений валов и 27 основных

Основные отклонения и поля допусков
Ранее было отмечено, что основное отклонение - это минимальное по абсолютной величине предельное отклонение. Графической интерпретацией основного отклонения является расстояние от нулевой линии до ближайшей границы поля допуска.
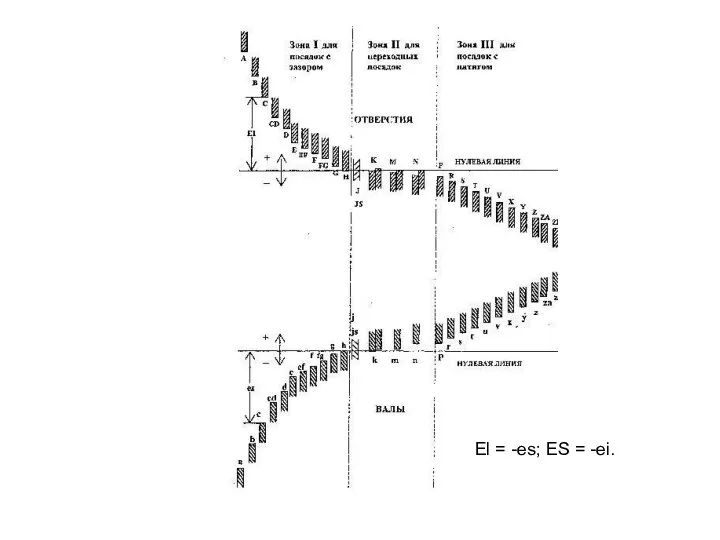
В ЕСДП основные отклонения обозначаются буквами латинского алфавита или сочетанием этих букв в количестве не более двух. Прописными буквами указываются основные отклонения для отверстий [сначала были А, В, С, D, Е, F, G, H, J, К, М, N, P, R, S, Т, U, V, X, Y, Z (21 наименование); затем добавились еще FG, EF, CD, ZA, ZB, ZC, JS (7 наименований)]. Строчными буквами - для валов [сначала были а, b, с, d, f, g, h, 3, k, m, n, p, r, s, t, u, v, x, y, z (21 наименование); затем добавились fg, et, cd, za, zb, zc, js (7 наименований)]. Система обозначений построена в алфавитном порядке.
Основные отклонения валов от а до h и отверстий от А до Н предназначены для образования посадок с зазором.
Основные отклонения валов от js до n и отверстий от JS до N предназначены для образования переходных посадок.
Основные отклонения валов от р до zc и отверстий от Р до ZC предназначены для образования посадок с натягом. Таким образом, первыми буквами (а; А) обозначены основные отклонения для посадки с наибольшими зазорами, а последними (zc; ZC) - для посадки с наибольшими натягами.
Слайд 14El = -es; ES = -ei.
El = -es; ES = -ei.
Слайд 15Третий принцип построения СДП
(Предусмотрены системы образования посадок)
Система отверстия и вала
В
Третий принцип построения СДП
(Предусмотрены системы образования посадок)
Система отверстия и вала
В
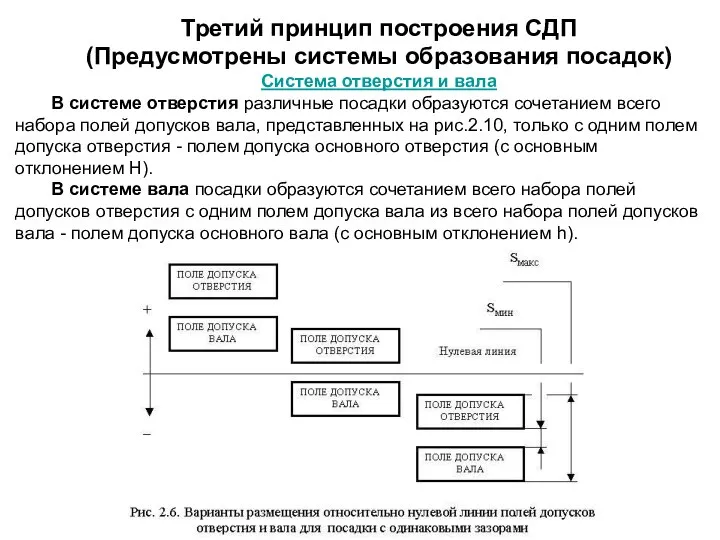
В системе вала посадки образуются сочетанием всего набора полей допусков отверстия с одним полем допуска вала из всего набора полей допусков вала - полем допуска основного вала (с основным отклонением h).
Слайд 16Сущность этих систем заключается в том, что при образовании всех трех видов
Сущность этих систем заключается в том, что при образовании всех трех видов

Основное отверстие - отверстие, нижнее отклонение которого равно нулю.
Основной вал - вал, верхнее отклонение которого равно нулю.
Таким образом, у основного отверстия с номинальным размером совпадает наименьший предельный размер, а у вала - наибольший предельный размер.
Существует два способа формирования посадок в системе отверстия и в системе вала.
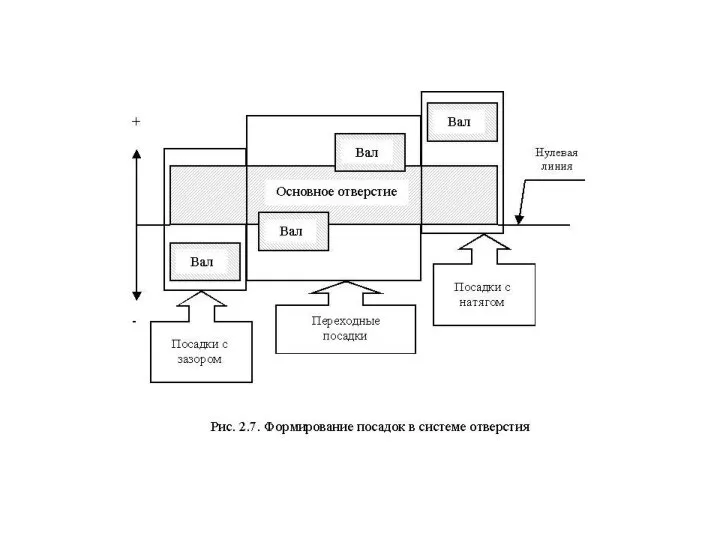
В системе отверстия посадки формируются изменением положения поля допуска вала относительно поля допуска основного отверстия (рис.2.7).
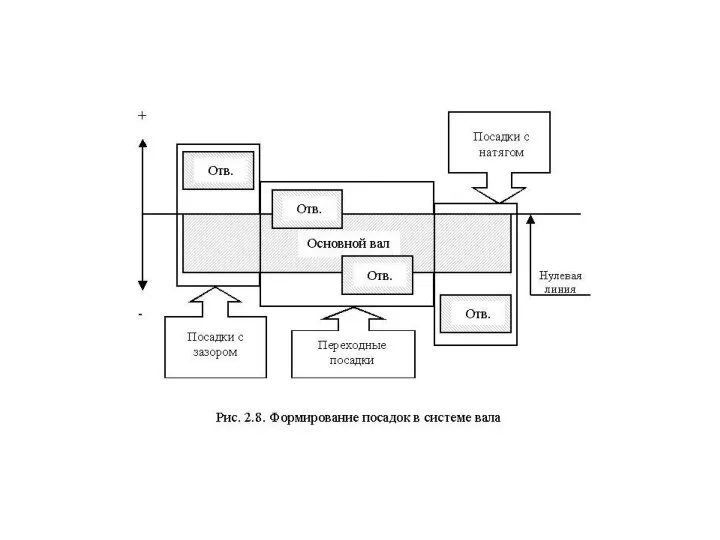
В системе вала посадки формируются изменением положения поля допуска отверстия относительно поля допуска основного вала (рис.2.8).
Слайд 19Система вала применяется в следующих случаях:
1. Когда на вал одного диаметра требуется
Система вала применяется в следующих случаях:
1. Когда на вал одного диаметра требуется
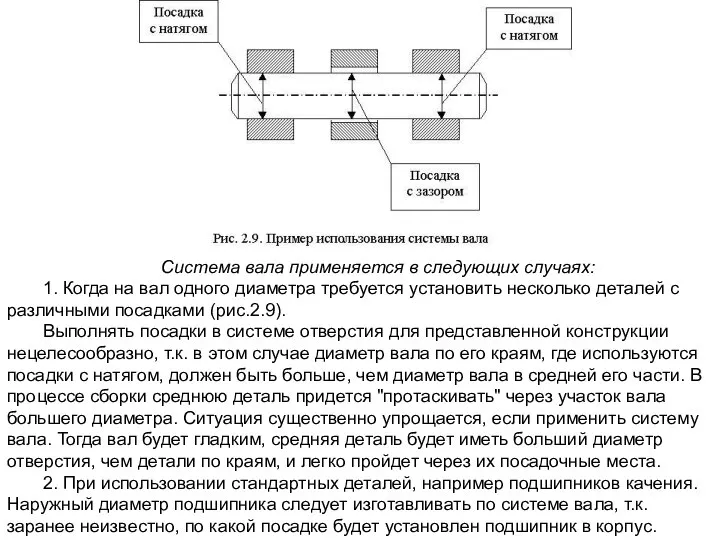
Выполнять посадки в системе отверстия для представленной конструкции нецелесообразно, т.к. в этом случае диаметр вала по его краям, где используются посадки с натягом, должен быть больше, чем диаметр вала в средней его части. В процессе сборки среднюю деталь придется "протаскивать" через участок вала большего диаметра. Ситуация существенно упрощается, если применить систему вала. Тогда вал будет гладким, средняя деталь будет иметь больший диаметр отверстия, чем детали по краям, и легко пройдет через их посадочные места.
2. При использовании стандартных деталей, например подшипников качения. Наружный диаметр подшипника следует изготавливать по системе вала, т.к. заранее неизвестно, по какой посадке будет установлен подшипник в корпус.
Слайд 20Четвертый принцип построения СДП
(установлена нормальная температура.)
+200С
Правила образования посадок
1. Посадки с
Четвертый принцип построения СДП
(установлена нормальная температура.)
+200С
Правила образования посадок
1. Посадки с

отверстия на квалитет грубее, чем вал.
2. Отверстия при прочих равных условиях изготавливаются с большими
погрешностями, чем валы, поэтому и допуск посадки делится не поровну, большая
часть отдается отверстию, меньшая - валу.
Слайд 21Посадки в ЕСДП и их обозначение на чертежах
В системе отверстия различные
Посадки в ЕСДП и их обозначение на чертежах
В системе отверстия различные

В системе вала посадки образуются сочетанием всего набора полей допусков отверстия с одним полем допуска вала из всего набора полей допусков вала - полем допуска основного вала (с основным отклонением h).
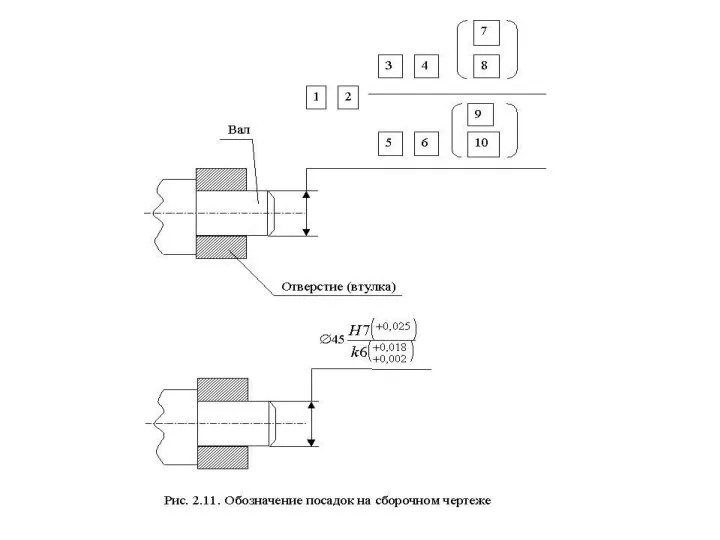
На сборочных чертежах посадки обозначаются дробью, представленной совокупностью цифр и букв латинского алфавита (рис.2.11).
Слайд 22Обозначение посадок на чертежах деталей
Обозначение посадок на чертежах деталей
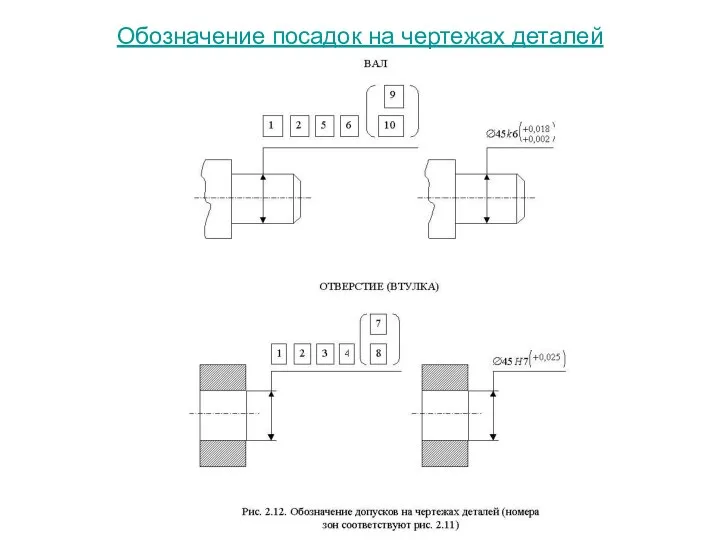
Слайд 24Здесь G - основное отклонение для отверстия: 7 - квалитет для отверстия;
Здесь G - основное отклонение для отверстия: 7 - квалитет для отверстия;

(основное отклонение для вала); 6 - квалитет для вала.
Для перевода посадок из одной системы в другую сохраняют квалитеты у отверстия и вала,
а основные отклонения заменяются, например:
Эти посадки совершенно одинаковые по своим характеристикам, т.к.:
максимальный диаметр отверстия (Dмакс):
40,034 мм | 40,025 мм
минимальный диаметр отверстия (Dмин):
40,009 мм | 40,0 мм
масимальный диаметр вала (dмакс):
40,000 мм | 39,991 мм
минимальный диаметр вала (dмин):
39,984 мм | 39,975 мм
максимальный зазор между отверстием и валом (Dмакс - dмин):
40,034 - 39,984 = 0,05 мм | 40,025 - 39,975 = 0,05 мм
минимальный зазор между отверстием и валом (Dмин - dмакс):
40,009 - 40,00 = 0,009 мм | 40,0 - 39,991 = 0,009 мм.
Слайд 25Посадки
Посадка - характер соединения деталей, определяемый значениями получающихся в нем зазоров
Посадки
Посадка - характер соединения деталей, определяемый значениями получающихся в нем зазоров

Зазор - разность между размерами отверстия и вала до сборки, если размер отверстия больше размера вала (обозначается S).
Натяг - разность размеров вала и отверстия до сборки, если размер вала больше размера отверстия (обозначается N).
Добавление в определениях слов "до сборки" объясняется тем, что в результате сборки может происходить деформация сопрягаемых поверхностей (при натяге).
В зависимости от свободы относительного перемещения сопрягаемых деталей или степени сопротивления взаимному смещению посадки разделяются на три вида:
- посадки с заром;
- посадки с натягом;
- переходные посадки.
Посадки с зазором
Посадка с зазором - посадка, при которой всегда образуется зазор в соединении,
т.е. наименьший предельный размер отверстия больше наибольшего размера
вала или равен ему.
Таким образом, в этих посадках при любых размерах отверстия и вала, находящихся в пределах допуска, гарантирован зазор.
Посадки с зазором характеризуются (отличаются одна от другой) значениями наибольшего и наименьшего зазоров, которые определяются так:
Sмакс = Dмакс - dмин = ES - ei; Sмин = Dмин - dмакс = El - es.
Слайд 26.
Dн = 105 мм.
ES = 0,035 мм.
EI = 0.
dн = 105
.
Dн = 105 мм.
ES = 0,035 мм.
EI = 0.
dн = 105
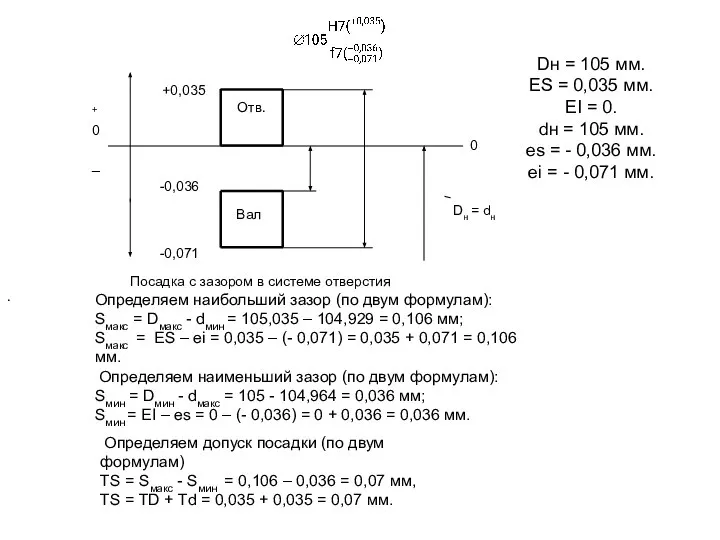
es = - 0,036 мм.
ei = - 0,071 мм.
Определяем наибольший зазор (по двум формулам):
Sмакс = Dмакс - dмин = 105,035 – 104,929 = 0,106 мм;
Sмакс = ES – ei = 0,035 – (- 0,071) = 0,035 + 0,071 = 0,106 мм.
Определяем наименьший зазор (по двум формулам):
Sмин = Dмин - dмакс = 105 - 104,964 = 0,036 мм;
Sмин = EI – es = 0 – (- 0,036) = 0 + 0,036 = 0,036 мм.
Определяем допуск посадки (по двум формулам)
TS = Sмакс - Sмин = 0,106 – 0,036 = 0,07 мм,
TS = TD + Td = 0,035 + 0,035 = 0,07 мм.
Слайд 27Посадки с натягом
Посадка с натягом - это посадка, при которой всегда
Посадки с натягом
Посадка с натягом - это посадка, при которой всегда

Посадка с натягом в системе отверстия
Посадки с натягом характеризуются (отличаются одна от другой) значением наименьшего и наибольшего натягов, которые определяются по следующим формулам:
Nмакс = dмакс - Dмин = es - EI; Nмин = dмин -Dмакс = ei - ES.
Слайд 28Переходные посадки
В этих посадках может образовываться как зазор, так и натяг.
Переходная
Переходные посадки
В этих посадках может образовываться как зазор, так и натяг.
Переходная
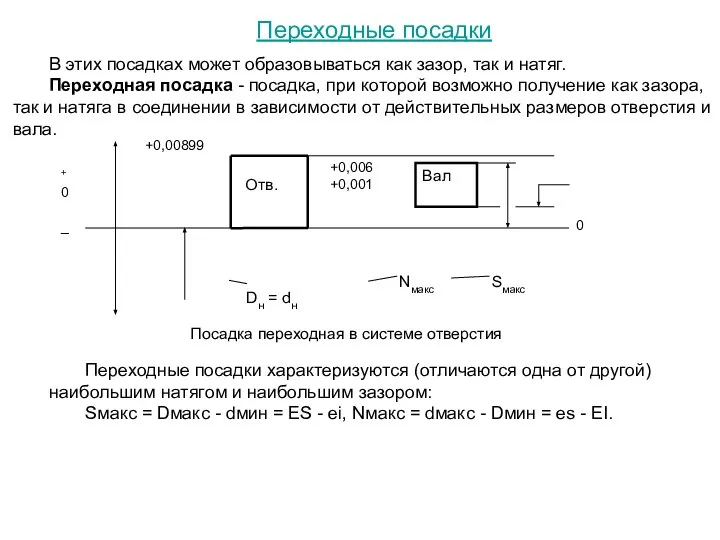
Переходные посадки характеризуются (отличаются одна от другой) наибольшим натягом и наибольшим зазором:
Sмакс = Dмакс - dмин = ES - ei, Nмакс = dмакс - Dмин = es - EI.
Слайд 29В практической деятельности используются предпочтительные поля допусков. Это в значительной мере способствует
В практической деятельности используются предпочтительные поля допусков. Это в значительной мере способствует
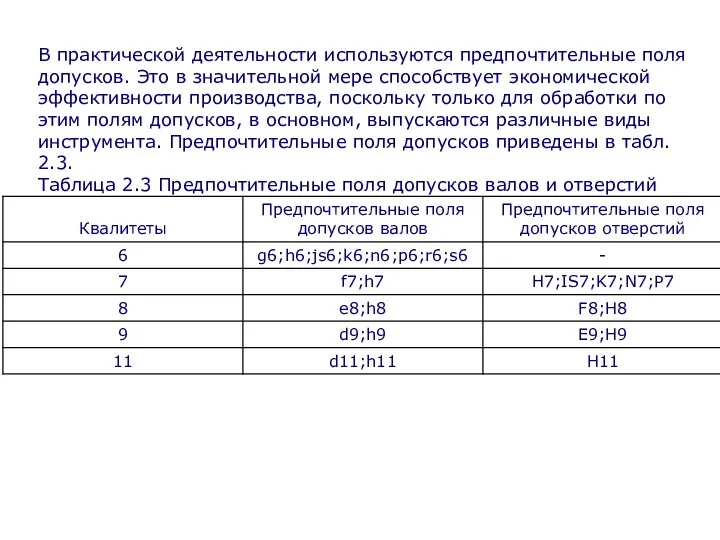
Таблица 2.3 Предпочтительные поля допусков валов и отверстий
Слайд 30Практические рекомендации по выбору посадок
Валы 4-5 квалитетов и отверстия 5-6 квалитетов
Практические рекомендации по выбору посадок
Валы 4-5 квалитетов и отверстия 5-6 квалитетов

Валы 6-7 и отверстия 7-8 квалитетов получаются, в основном, тонким точением или растачиванием (алмазным), чистовым развертыванием, чистовым протягиванием, притиркой, хонингованием плоскости, холодной штамповкой в вырубных штампах.
Валы 8-9 и отверстия 9 квалитета получают тонким строганием, получистовым развертыванием, тонким шабрением, холодной штамповкой в вытяжных штампах
Валы и отверстия 10 квалитета получают чистовым зенкерованием и способами, применяемыми для обработки по 9 квалитету.
Валы и отверстия 11 квалитета получаются чистовым строганием, чистовым фрезерованием, чистовым обтачиванием, сверлением по кондуктору, литьем по выплавляемым моделям.
Валы и отверстия 12 и 13 квалитетов получают черновым строганием, чистовым долблением, черновым фрезерованием, сверлением без кондуктора, черновым зенкерованием, получистым растачиванием.
Валы и отверстия 14-17 квалитетов получают отрезкой ножницами и пилами, автоматической газовой резкой, отрезкой резцом и фрезой, черновым долблением, литьем в песчаные формы.
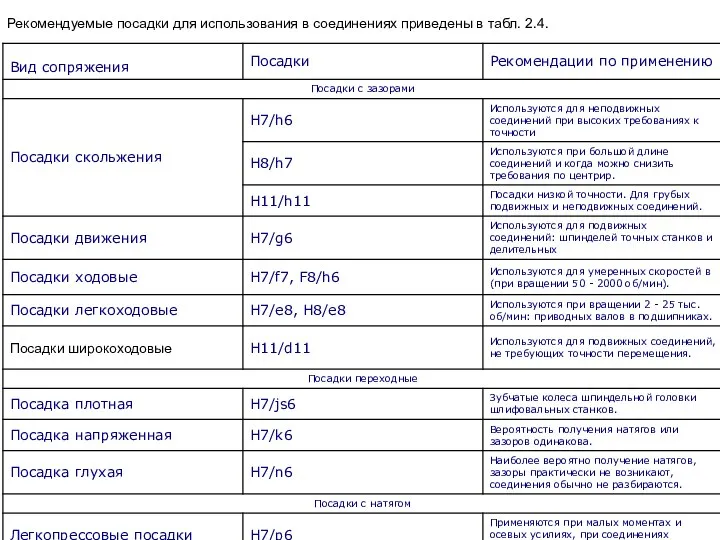
Слайд 31Рекомендуемые посадки для использования в соединениях приведены в табл. 2.4.
Рекомендуемые посадки для использования в соединениях приведены в табл. 2.4.
Слайд 32Калибры. Требования к точности и контроль деталей калибрами
Годность деталей с допуском
Калибры. Требования к точности и контроль деталей калибрами
Годность деталей с допуском
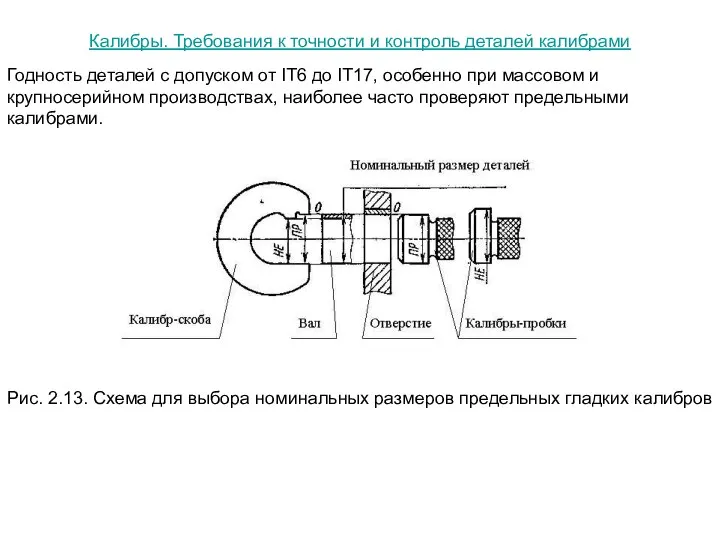
Рис. 2.13. Схема для выбора номинальных размеров предельных гладких калибров
Слайд 33НОРМИРОВАНИЕ ТОЧНОСТИ ФОРМЫ И РАСПОЛОЖЕНИЯ ПОВЕРХНОСТЕЙ
ДЕТАЛЕЙ
Отклонение формы поверхностей
Отклонением формы
НОРМИРОВАНИЕ ТОЧНОСТИ ФОРМЫ И РАСПОЛОЖЕНИЯ ПОВЕРХНОСТЕЙ
ДЕТАЛЕЙ
Отклонение формы поверхностей
Отклонением формы

Профиль - это линия пересечения поверхностей. Профилем может быть прямая линия. В частном случае профиль - это линия пересечения с плоско-стью. Наиболее часто в машиностроении профиль рассматривается в плос-кости, перпендикулярной к поверхности.
Допуск формы - это величина, в пределах которой может изменяться от-клонение формы.
Будем использовать следующие обозначения:
ЕF - отклонение формы; ТF - допуск формы; L - длина участка, на котором определяется отклонение.
Отсчет отклонений формы или профиля производится от прилегающей плоскости или прилегающего профиля.
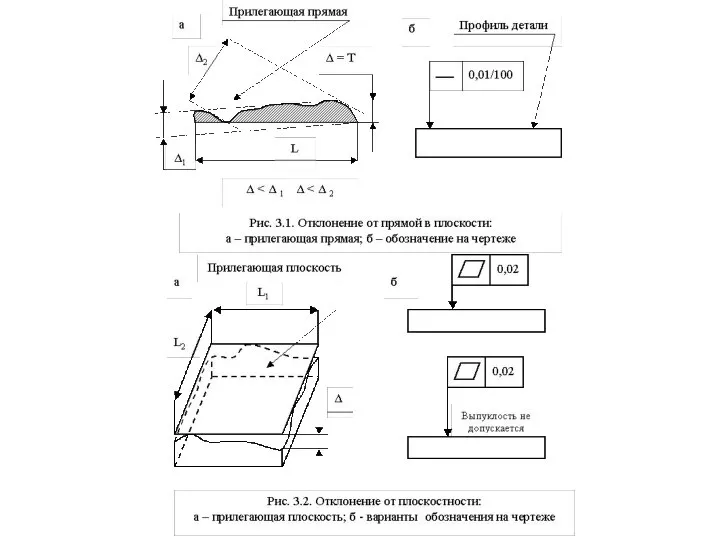
Виды и обозначение отклонений формы приведены в табл.3.1.
Слайд 34Отсчет этого отклонения производится от точек реального профиля до прилегающей прямой. Прилегающей
Отсчет этого отклонения производится от точек реального профиля до прилегающей прямой. Прилегающей

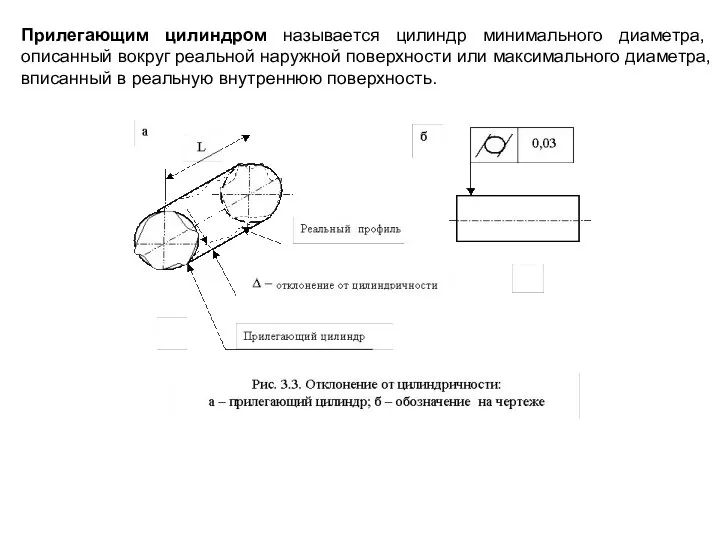
Слайд 36Прилегающим цилиндром называется цилиндр минимального диаметра, описанный вокруг реальной наружной поверхности или
Прилегающим цилиндром называется цилиндр минимального диаметра, описанный вокруг реальной наружной поверхности или
Слайд 39Таким образом, отклонение от прямолинейности в плоскости - это наибольшее расстояние Δ
Таким образом, отклонение от прямолинейности в плоскости - это наибольшее расстояние Δ

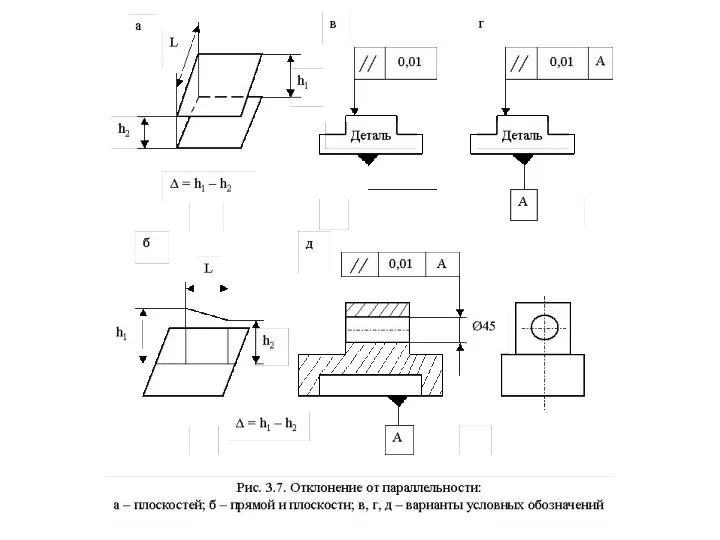
Отклонение от плоскостности - это наибольшее расстояние Δ от точек реальной поверхности до прилегающей плоскости.
Отклонение от цилиндричности - это максимальное расстояние Δ от точек реальной поверхности до прилегающего цилиндра.
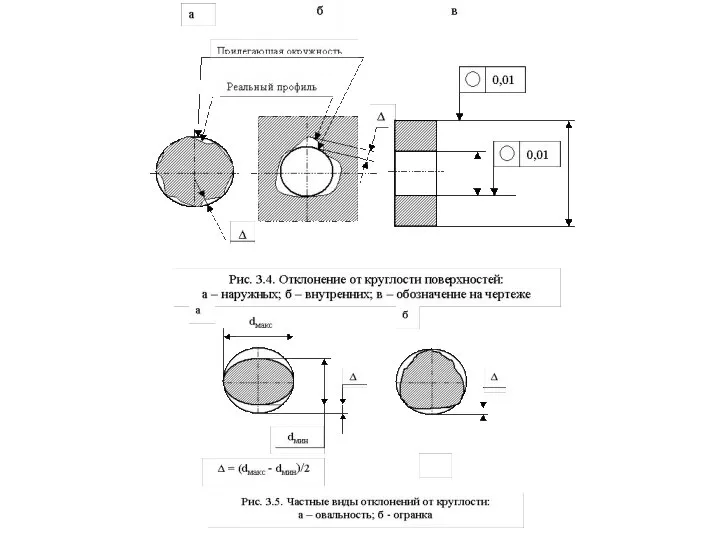
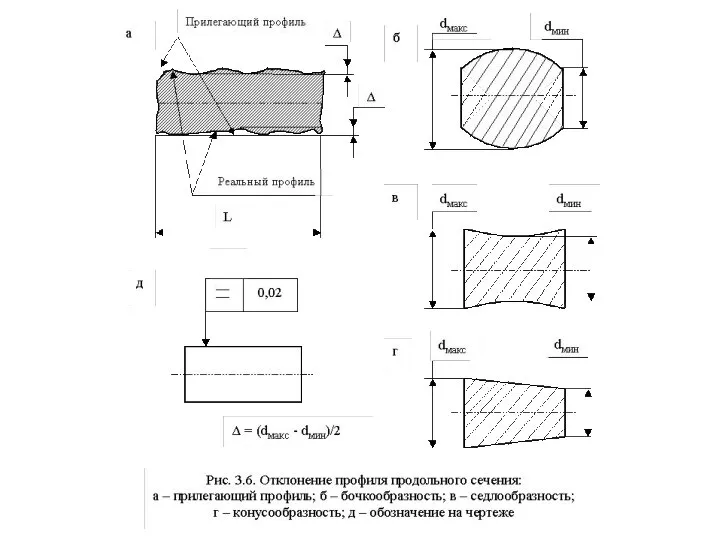
Отклонение от круглости - это максимальное расстояние Δ от точек реального профиля до прилегающей окружности. Этим показателем опре-деляется отклонение формы цилиндрических деталей в плоскости, перпендикулярной оси симметрии.
Отклонение профиля продольного сечения - это максимальное расстояние от точек образующих реальной поверхности, лежащих в плоскости, проходящих через ее ось симметрии, до соответствующей стороны прилегающего профиля.
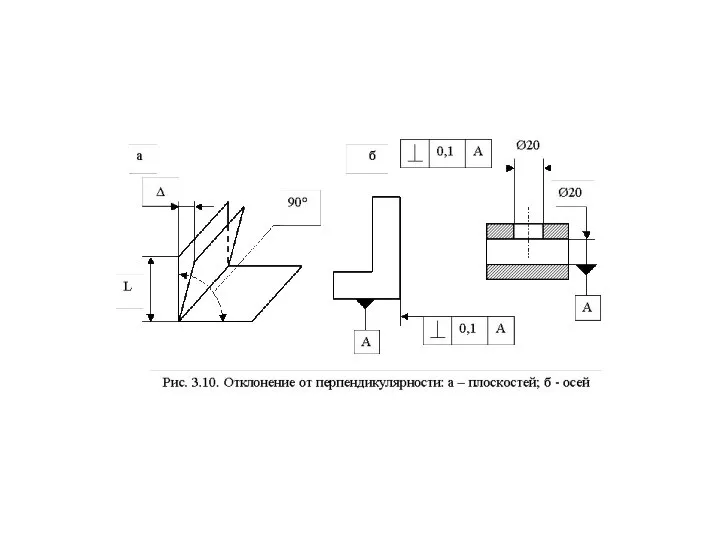
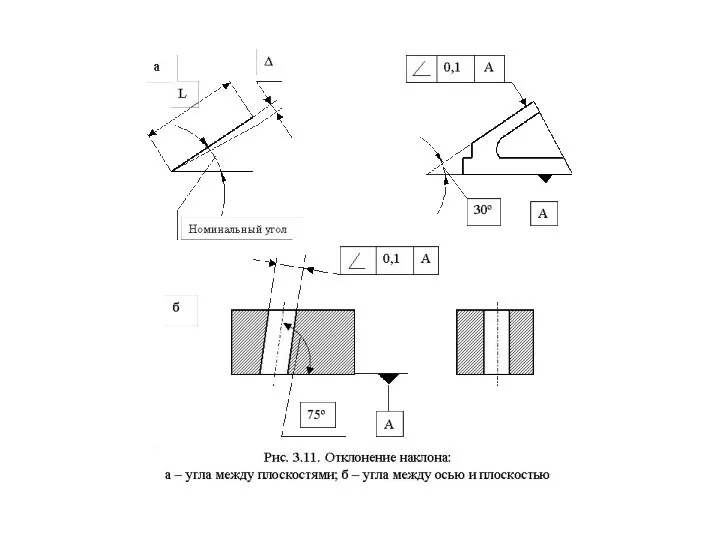
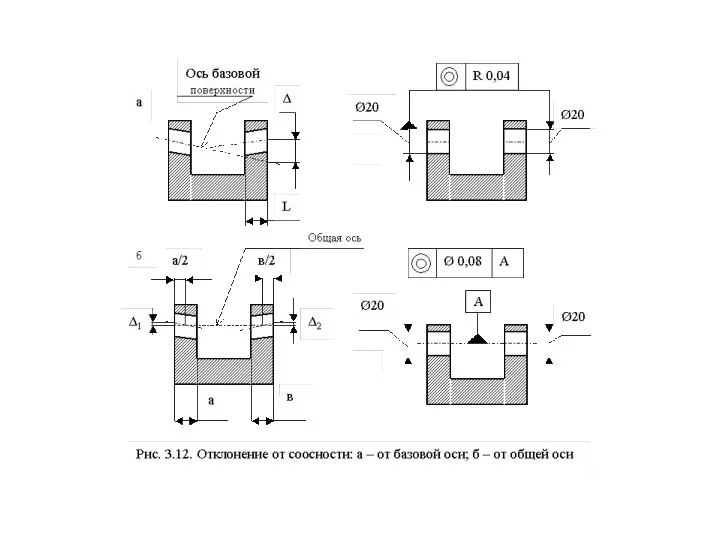
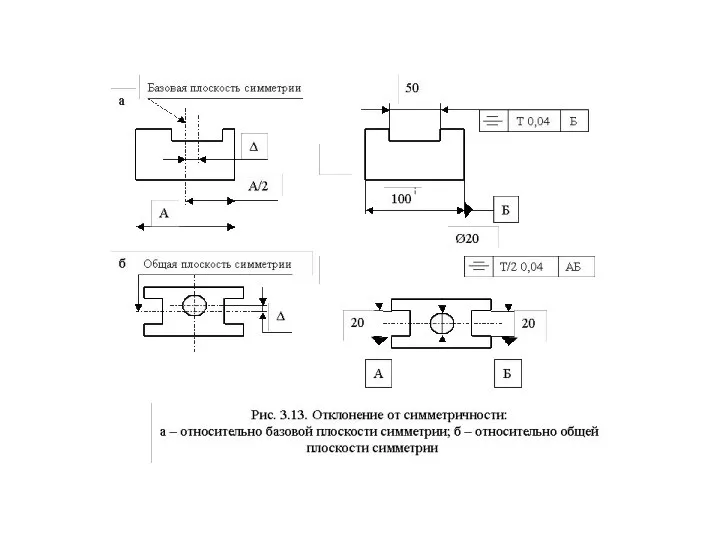
Слайд 40Отклонения расположения поверхностей
Отклонение расположения поверхности или профиля детали - это отклонение
Отклонения расположения поверхностей
Отклонение расположения поверхности или профиля детали - это отклонение

Слайд 49Суммарные отклонения формы и расположения поверхностей
Допускается использовать любые сочетания отклонений формы
Суммарные отклонения формы и расположения поверхностей
Допускается использовать любые сочетания отклонений формы

Однако есть такие сочетания отклонений, которые постоянно используются при нормировании точности деталей цилиндрической формы.
Для этих сочетаний установлены специальные знаки. Эти отклонения и знаки, которыми они обозначены, рассмотрены ниже.
Слайд 52Отклонение формы заданного профиля или поверхности - это наибольшее отклонение точек реального
Отклонение формы заданного профиля или поверхности - это наибольшее отклонение точек реального
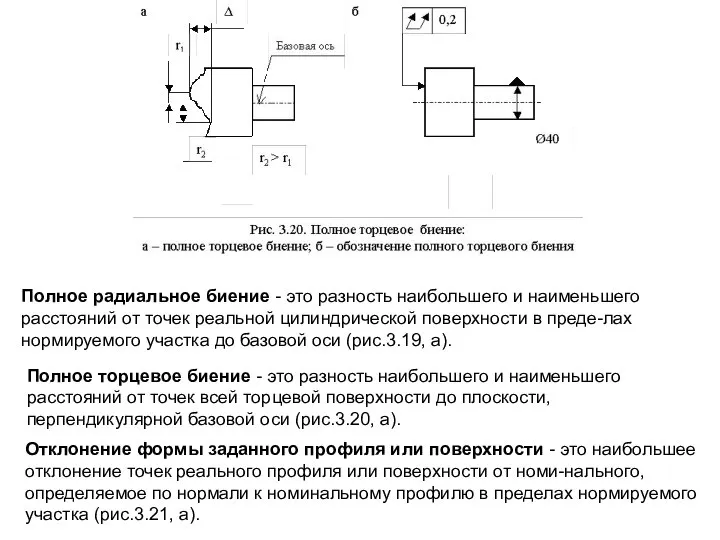
Полное торцевое биение - это разность наибольшего и наименьшего расстояний от точек всей торцевой поверхности до плоскости, перпендикулярной базовой оси (рис.3.20, а).
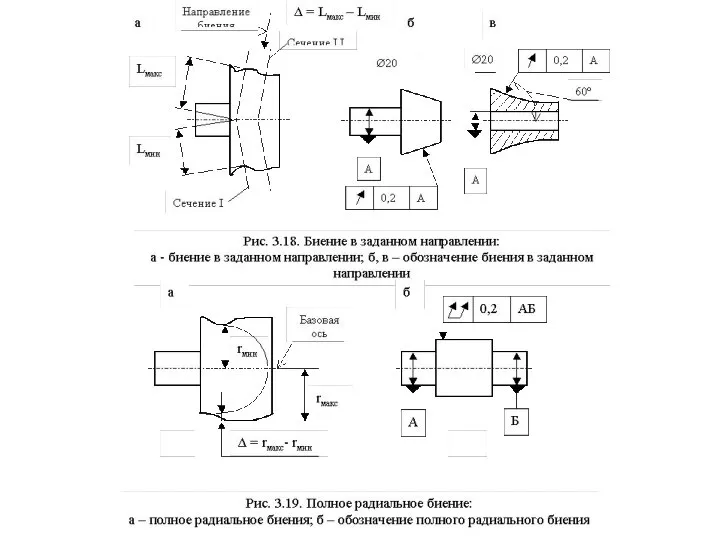
Полное радиальное биение - это разность наибольшего и наименьшего расстояний от точек реальной цилиндрической поверхности в преде-лах нормируемого участка до базовой оси (рис.3.19, а).
Слайд 54Радиальное биение - это разность наибольшего и наименьшего расстояний от точек реального
Радиальное биение - это разность наибольшего и наименьшего расстояний от точек реального

Радиальное биение является суммой отклонений от круглости и соосности.
Торцевое биение - это разность наибольшего и наименьшего расстояний от точек реального профиля торцевой поверхности до плоскости пер-пендикулярной базовой оси, измеренной на определенном (заданном) диаметре (рис.3.17, а).
Биение в заданном направлении - это разность наибольшего и наименьшего расстояний от точек реального профиля поверхности вращения в сечении этой поверхности конусом, ось которого совпадает с базовой осью, а образующая параллельна направлению биения (рис.3.18, а).
Торцевое биение является суммой отклонений от плоскостности и перпендикулярности.
Биение в заданном направлении является суммой отклонений от круглости и соосности.
Для того чтобы определить полное торцевое биение, надо найти в пределах всей нормируемой торцевой поверхности наибольшее и наименьшее расстояния до плоскости, перпендикулярной базовой оси и взять их разность. В то время как торцевое биение определяется как разность наибольшего и наименьшего расстояний до вышеуказанной плоскости для той окружности в пределах нормируемой торцевой поверхности, где эта разность имеет максимальное значение. Полное торцевое биение является суммой отклонений от плоскостности и перпендикулярности.
Слайд 55Зависимые отклонения и допуски формы и расположения поверхностей
Отклонения формы и расположения поверхностей
Зависимые отклонения и допуски формы и расположения поверхностей
Отклонения формы и расположения поверхностей
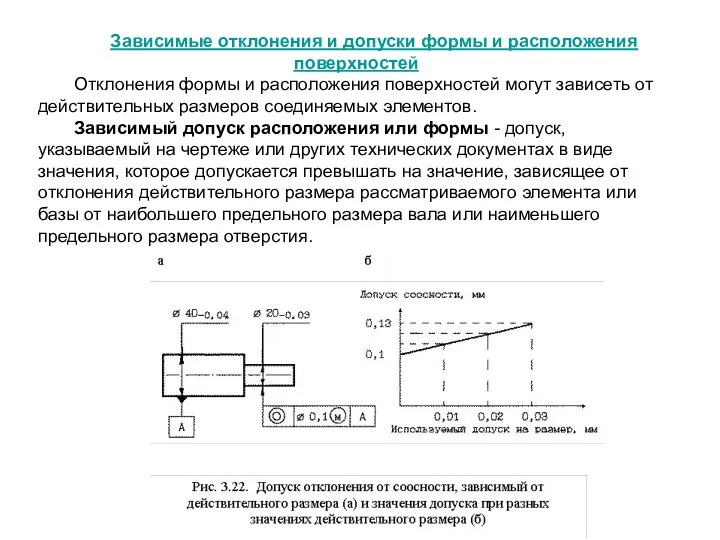
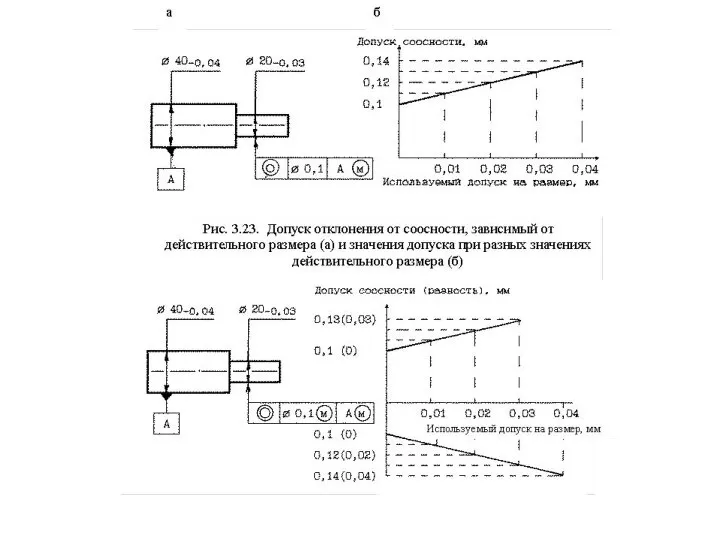
Зависимый допуск расположения или формы - допуск, указываемый на чертеже или других технических документах в виде значения, которое допускается превышать на значение, зависящее от отклонения действительного размера рассматриваемого элемента или базы от наибольшего предельного размера вала или наименьшего предельного размера отверстия.
Слайд 56Итак, зависимое отклонение (допуск) формы и расположения поверхностей - это отклонение (допуск),
Итак, зависимое отклонение (допуск) формы и расположения поверхностей - это отклонение (допуск),

Так, если диаметры вала сделаны по наименьшим предельным размерам, т.е. 19,97 мм и 39,96 мм, то допуск на соосность будет равен:
0,1 (заданный) +0,03 (при O19,97) +0,04 (при O39,96) = 0,17 мм.
Слайд 58Числовые значения отклонений (допусков) формы и расположения поверхностей
Согласно ГОСТ 24643 (Основные
Числовые значения отклонений (допусков) формы и расположения поверхностей
Согласно ГОСТ 24643 (Основные

Установлено три уровня зависимости отклонений от допуска размера в процентах; А - нормальная точность, когда отклонение составляет примерно
60% от допуска размера; В - повышенная точность, когда отклонение
составляет примерно 40% от допуска размера; С - высокая точность, когда отклонение составляет 25% от допуска размера.
Отклонения от формы цилиндрической поверхности (отклонение от круглости, радиальное биение и полное радиальное биение), соответствующие указанным уровням, составляют примерно 30, 20 и 12% допуска размера, т.к. в данном
случае нормируется отклонение радиуса цилиндрической поверхности.
Слайд 59НОРМИРОВАНИЕ ТРЕБОВАНИЙ К НЕРОВНОСТЯМ НА ПОВЕРХНОСТИ ЭЛЕМЕНТОВ ДЕТАЛЕЙ (ШЕРОХОВАТОСТЬ ПОВЕРХНОСТИ)
Шероховатостью поверхности
НОРМИРОВАНИЕ ТРЕБОВАНИЙ К НЕРОВНОСТЯМ НА ПОВЕРХНОСТИ ЭЛЕМЕНТОВ ДЕТАЛЕЙ (ШЕРОХОВАТОСТЬ ПОВЕРХНОСТИ)
Шероховатостью поверхности
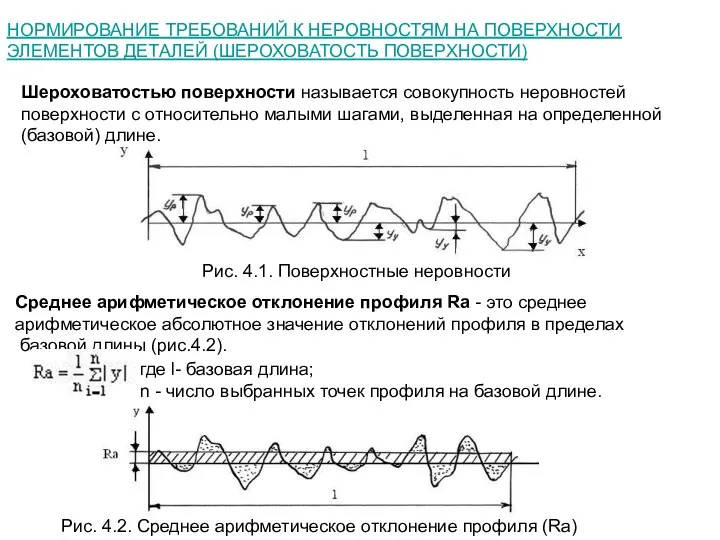
Рис. 4.1. Поверхностные неровности
Среднее арифметическое отклонение профиля Ra - это среднее арифметическое абсолютное значение отклонений профиля в пределах
базовой длины (рис.4.2).
где l- базовая длина;
n - число выбранных точек профиля на базовой длине.
Рис. 4.2. Среднее арифметическое отклонение профиля (Ra)
Слайд 60 Высота неровностей по десяти точкам
Высота неровностей по десяти точкам Rz
Высота неровностей по десяти точкам
Высота неровностей по десяти точкам Rz
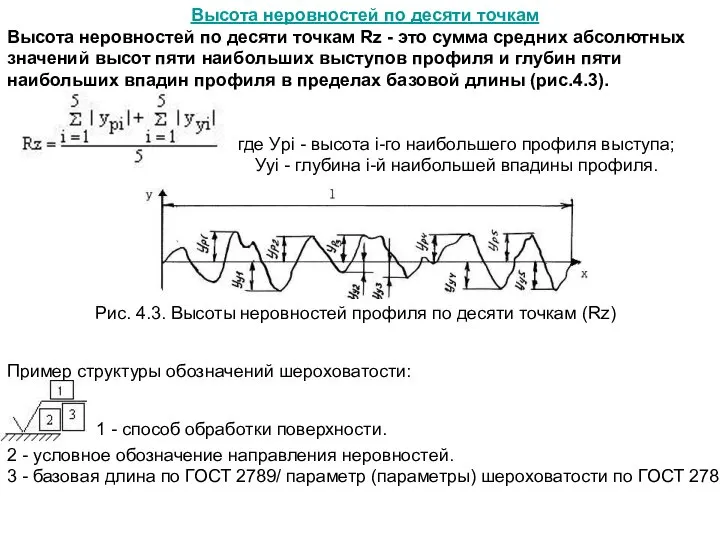
где Уpi - высота i-го наибольшего профиля выступа;
Уyi - глубина i-й наибольшей впадины профиля.
Рис. 4.3. Высоты неровностей профиля по десяти точкам (Rz)
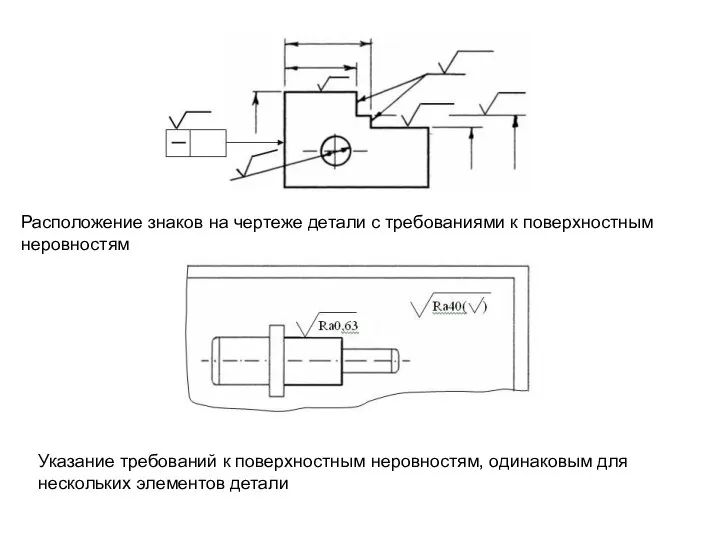
Пример структуры обозначений шероховатости:
1 - способ обработки поверхности.
2 - условное обозначение направления неровностей.
3 - базовая длина по ГОСТ 2789/ параметр (параметры) шероховатости по ГОСТ 2789.
Слайд 61Указание требований к поверхностным неровностям, одинаковым для нескольких элементов детали
Расположение знаков
Указание требований к поверхностным неровностям, одинаковым для нескольких элементов детали
Расположение знаков
Слайд 62Таблица 4.1 Соотношение между параметрами шероховатости
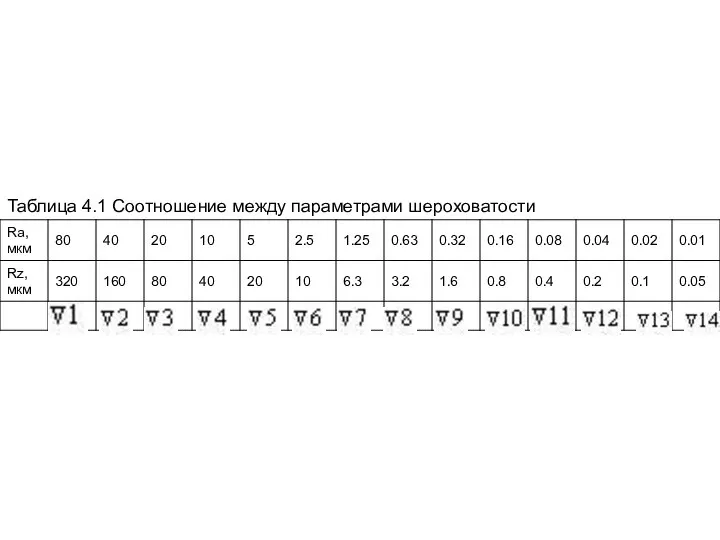
Таблица 4.1 Соотношение между параметрами шероховатости
Слайд 63НОРМИРОВАНИЕ ТОЧНОСТИ ДЕТАЛЕЙ, СОПРЯГАЕМЫХ С ПОДШИПНИКАМИ КАЧЕНИЯ
Подшипник - это деталь или
НОРМИРОВАНИЕ ТОЧНОСТИ ДЕТАЛЕЙ, СОПРЯГАЕМЫХ С ПОДШИПНИКАМИ КАЧЕНИЯ
Подшипник - это деталь или

По принципу работы подшипники разделяются на подшипники скольжения и качения. Подшипники скольжения образуют комплект цилиндрических или сферических поверхностей и работают в условиях жидкостного, смешанного или сухого трения.
Подшипники качения изготавливаются специализированной отраслью промышленности, в которой имеются отличия от других отраслей машиностроения в отношении некоторых вопросов нормирования точности.
Подшипник качения - это стандартный узел, обладающий внешней взаимозаменяемостью своими присоединительными поверхностями; D - наружный диаметр наружного кольца (рис.5.1), d - внутренний диаметр внутреннего кольца, В - ширина (высота) колец подшипника при одинаковой ширине наружного и внутреннего колец.
Установлено несколько классов точности подшипников (ГОСТ 520) в зависимости от используемых тел качения и от направления воспринимаемой нагрузки:
классы 0, 6, 5, 4, 2, Т - для шариковых и роликовых.
классы 0, 6, 5, 4, 2 - для упорных и упорно-радиальных подшипников;
классы 0, 6Х, 6, 5, 4, 2 - для роликовых конических подшипников.
Наиболее грубым является класс 0, а наиболее точными - классы 2 и Т. Помимо этих классов, нормируются дополнительные, более грубые классы 8 и 7, по точности ниже, чем класс 0. Эти классы поставляются по заказам потребителей.
Слайд 64Класс точности подшипника характеризуется целым комплексом точностных требований, относящихся к отклонениям размеров,
Класс точности подшипника характеризуется целым комплексом точностных требований, относящихся к отклонениям размеров,

1. Требования к точности присоединительных размеров D, d, В, отклонений формы и расположения поверхностей колец и тел вращения, шероховатости присоединительных поверхностей.
2. Радиальное и торцевое (осевое) биение либо подшипника в сборе, либо отдельных колец.
Помимо класса точности для подшипников качения устанавливают три категории А, В и С в зависимости от нормирования других показателей точности, являющихся дополнительными к основным точностным требованиям.
К категории А относятся подшипники классов точности 5, 4, 2, Т, если к ним предъявляются дополнительные повышенные требования в отношении вибрации или в отношении волнистости и отклонения от круглости и волнистости поверхности качения и т.д.
К категории В относятся подшипники классов точности 0, 6Х, 6, 5, для которых нормируется дополнительно одно из требований, например регламентируются требования в отношении вибрации и т.д. аналогично категории А.
К категории С относятся подшипники классов точности 8, 7, 0, 6, к которым не предъявляются требования по уровню вибраций, момента трения и другим требованиям.
Слайд 651. Требования к точности присоединительных размеров D, d, В, отклонений формы и
1. Требования к точности присоединительных размеров D, d, В, отклонений формы и

2. Радиальное и торцевое (осевое) биение либо подшипника в сборе, либо отдельных колец.
Помимо класса точности для подшипников качения устанавливают три категории А, В и С в зависимости от нормирования других показателей точности, являющихся дополнительными к основным точностным требованиям.
К категории А относятся подшипники классов точности 5, 4, 2, Т, если к ним предъявляются дополнительные повышенные требования в отношении вибрации или в отношении волнистости и отклонения от круглости и волнистости поверхности качения и т.д.
К категории В относятся подшипники классов точности 0, 6Х, 6, 5, для которых нормируется дополнительно одно из требований, например регламентируются требования в отношении вибрации и т.д. аналогично категории А.
К категории С относятся подшипники классов точности 8, 7, 0, 6, к которым не предъявляются требования по уровню вибраций, момента трения и другим требованиям.
Слайд 66Посадки подшипников качения
Поля допусков колец подшипников качения
Классы точности подшипников качения
Посадки подшипников качения
Поля допусков колец подшипников качения
Классы точности подшипников качения

Основное отклонение посадочных мест колец подшипников обозначается буквой L для диаметра отверстия (внутреннего кольца подшипника), а основное отклонение вала (наружного кольца подшипника) - буквой 1.
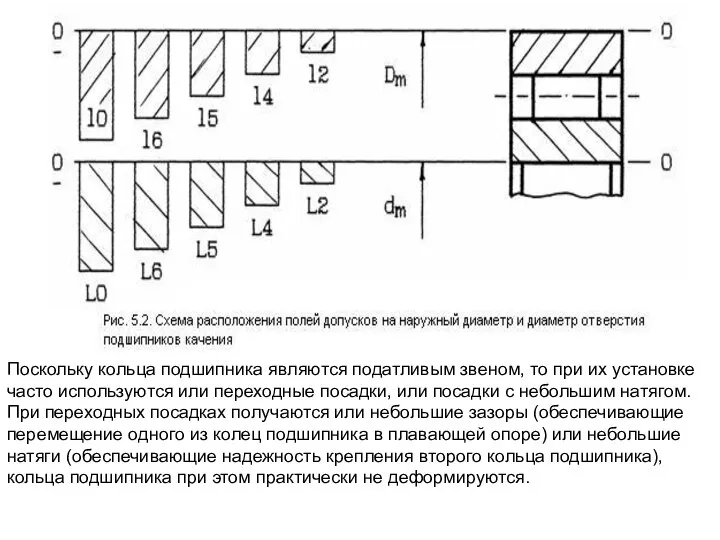
Для среднего диаметра отверстия подшипника (внутреннего кольца подшипника) установлены поля допусков LO, L6, L5, L4, L2.
Для среднего диаметра вала (наружного кольца подшипника) установлены поля допусков 10, 16, 15, 14, 12 (рис. 5.2).
Поле допуска для среднего диаметра наружного кольца Dm расположено, как и поле допуска основного вала, в системе допусков и посадок, т.е. "в тело" вала (в минус).
Расположение поля допуска для среднего диаметра dm кольца (внутреннего диаметра) отличается от расположения поля допуска для основного отверстия в системе допусков и посадок (поле допуска для внутреннего кольца подшипника dm также расположено в минус, как для вала, т.е. "из тела" детали, а в системе допусков и посадок для основного отверстия поле допуска расположено со знаком плюс).
Слайд 67Поскольку кольца подшипника являются податливым звеном, то при их установке часто используются
Поскольку кольца подшипника являются податливым звеном, то при их установке часто используются
Слайд 68Поля допусков для размеров посадочных поверхностей валов и отверстий корпусов под подшипники
Поля допусков для размеров посадочных поверхностей валов и отверстий корпусов под подшипники

Таблица 5.1 Поля допусков валов для основных видов сопряжений по внутреннему кольцу подшипника
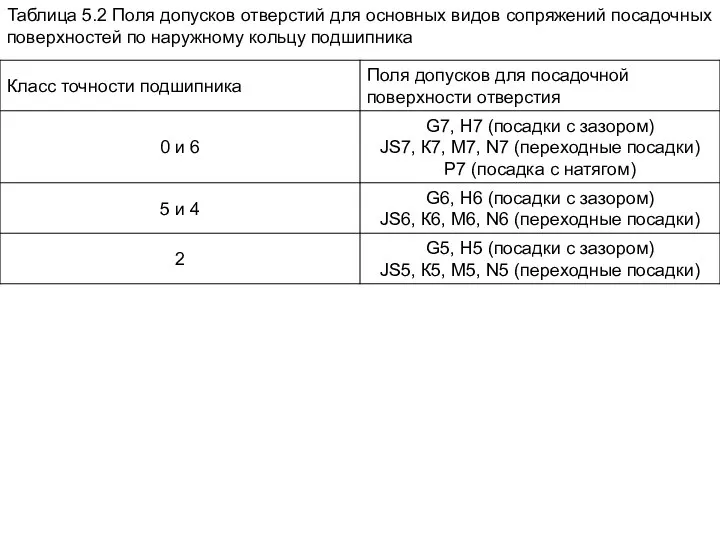
Слайд 69Таблица 5.2 Поля допусков отверстий для основных видов сопряжений посадочных поверхностей по
Таблица 5.2 Поля допусков отверстий для основных видов сопряжений посадочных поверхностей по
Слайд 70Посадки подшипников качения на валы и отверстия корпусов
Посадки по наружному диаметру
Посадки подшипников качения на валы и отверстия корпусов
Посадки по наружному диаметру
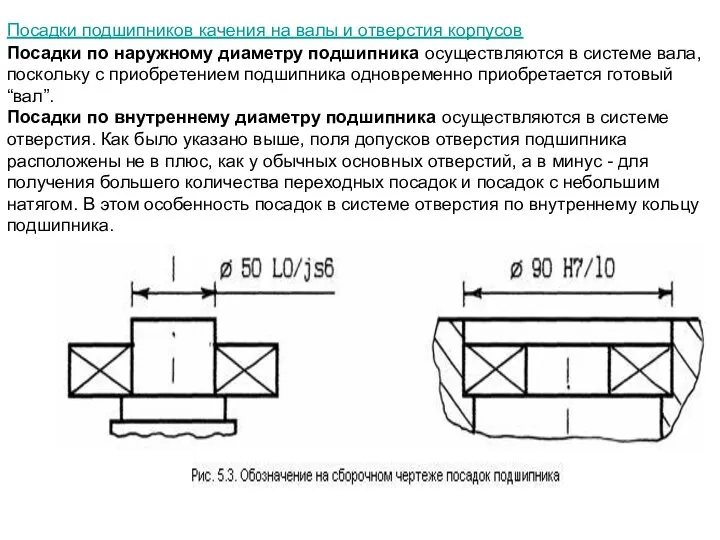
Посадки по внутреннему диаметру подшипника осуществляются в системе отверстия. Как было указано выше, поля допусков отверстия подшипника расположены не в плюс, как у обычных основных отверстий, а в минус - для получения большего количества переходных посадок и посадок с небольшим натягом. В этом особенность посадок в системе отверстия по внутреннему кольцу подшипника.
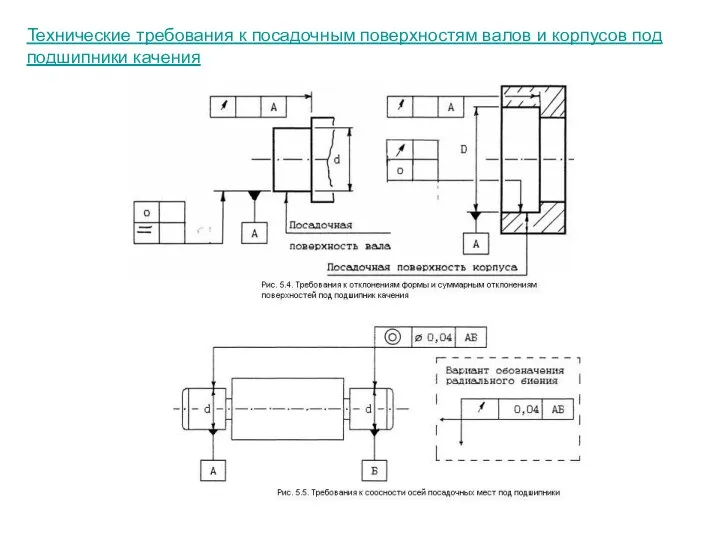
Слайд 71Технические требования к посадочным поверхностям валов и корпусов под подшипники качения
Технические требования к посадочным поверхностям валов и корпусов под подшипники качения
Слайд 72Выбор посадок для колец подшипников
Рекомендации при выборе посадок подшипников
Нельзя устанавливать
Выбор посадок для колец подшипников
Рекомендации при выборе посадок подшипников
Нельзя устанавливать

Вращающееся кольцо (на валу или в корпусе) должно устанавливаться с гарантированным натягом.
При двухопорном вале (два подшипника на концах вала) посадка одного из невращающихся колец должна быть с гарантированным зазором для компенсации температурных деформаций вала или корпуса.
Таблица 5.3 Шероховатость по параметру Ra для посадочных мест
Слайд 73Кольца подшипника во время работы могут испытывать различные виды нагружений.
Бывают следующие виды
Кольца подшипника во время работы могут испытывать различные виды нагружений.
Бывают следующие виды

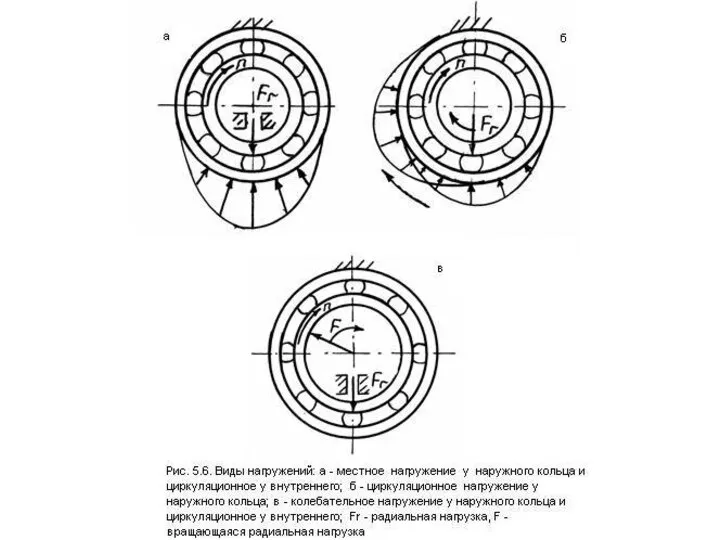
Местное нагружение - такой вид нагружения, при котором действующая на подшипник результирующая радиальная нагрузка постоянно воспринимается одним и тем же ограниченным участком дорожки качения кольца и передается соответствующему участку посадочной поверхности вала или корпуса (рис.5.6, а). Кольца, которые подвергаются местному нагружению, должны устанавливаться с гарантированным зазором или по переходной посадке при минимальном натяге.
Циркуляционным нагружением колец называется такой вид нагружения, при котором действующая на подшипник результирующая радиальная нагрузка воспринимается и передается телами качения в процессе вращения последовательно по всей длине дорожки качения, а, следовательно, и по всей посадочной поверхности вала или корпуса (рис.5.6, б).
Колебательным нагружением кольца называется такой вид нагружения, при котором неподвижное кольцо подшипника подвергается одновременно воздействию радиальной нагрузки, постоянной по направлению, и вращаю-щейся, меньшей или равной по значению. Их равнодействующая совершает периодическое колебательное движение, симметричное относительно неподвижной силы, причем она периодически воспринимается и передается соответствующему участку посадочной поверхности (рис.5.6,в).
Слайд 75НОРМИРОВАНИЕ ТОЧНОСТИ ШПОНОЧНЫХ СОЕДИНЕНИЙ
Шпоночное соединение вала с установленным на нем отверстием
НОРМИРОВАНИЕ ТОЧНОСТИ ШПОНОЧНЫХ СОЕДИНЕНИЙ
Шпоночное соединение вала с установленным на нем отверстием
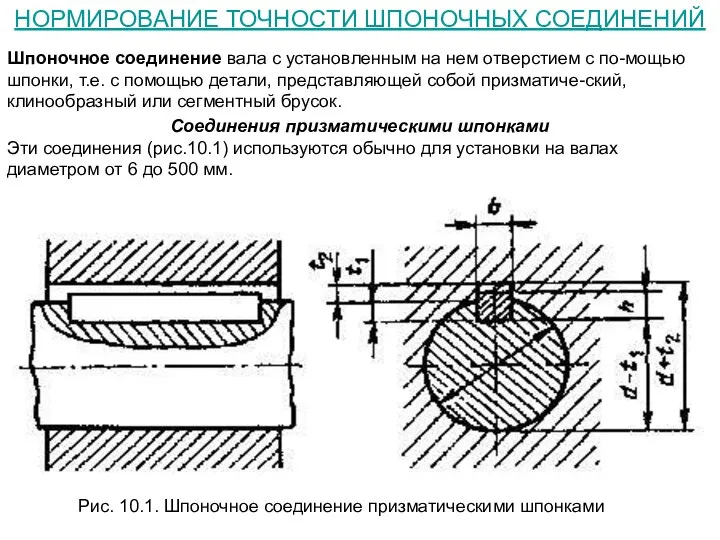
Соединения призматическими шпонками
Эти соединения (рис.10.1) используются обычно для установки на валах диаметром от 6 до 500 мм.
Рис. 10.1. Шпоночное соединение призматическими шпонками
Слайд 76Глубина пазов под шпонку у валов t1 - от 1,2 до 31
Глубина пазов под шпонку у валов t1 - от 1,2 до 31

Допускаемые отклонения на размер глубины пазов вала и втулки нормируются одинаковыми с плюсовым отклонением, а при нормировании с учетом диаметра отклонение для вала берется со знаком "минус".
Б. Нормирование точности размеров элементов шпоночного соединения аналогично гладким сопряжениям в виде полей допусков на сопрягаемые элементы. Эти поля допусков взяты из ГОСТ 25347, соответственно для отверстий и валов.
1. Нормирование точности шпонок ("валов" - охватываемых размеров) производится в зависимости от их габаритных размеров. Для ширины шпонки b нормируется одно поле допуска h9, для высоты h - обычно поле допуска h11 и h9 (для шпонок высотой от 2 до 6 мм соответственно) и для длины 1 - поле допуска hl4. (Дается одно поле допуска и обозначение поля допуска как для основного вала, так как деталь (шпонка) с наружной - (охватываемой) поверхностью).
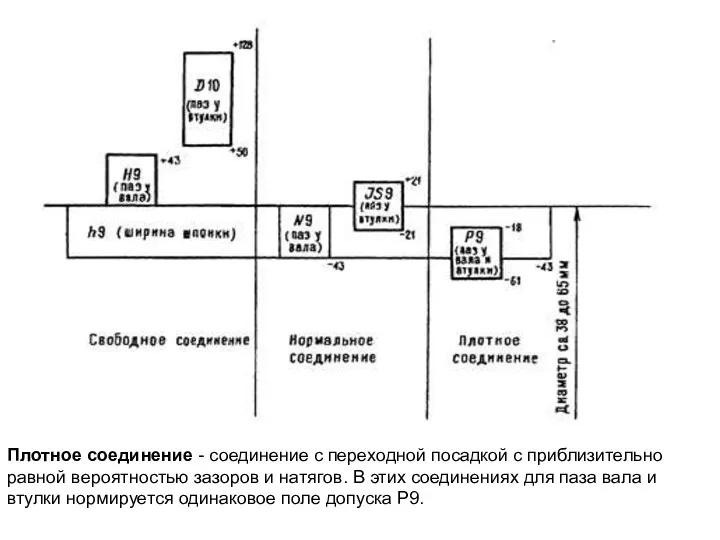
2. Нормирование точности шпоночных пазов на валу и во втулке ("отверстия") осуществляется в зависимости от вида соединений, которые разделяются на три группы с различными требованиями к размерам ширины пазов. На рис.10.2 приведены схемы полей допусков шпоночного соединения для конкретных размеров (d 38-65 мм).
Свободное соединение - соединение с гарантированным зазором. Для этих соединений задается поле допуска Н9 для ширины паза на валу и D10 - и на втулке.
Нормальное соединение - соединение с переходной посадкой с большей вероятностью получения зазора. Для этих соединений поле допуска N9 задается для паза на валу и JS9 - на втулке.
Слайд 77Плотное соединение - соединение с переходной посадкой с приблизительно равной вероятностью зазоров
Плотное соединение - соединение с переходной посадкой с приблизительно равной вероятностью зазоров
Слайд 78Иногда шпоночные соединения разделяют на затяжные, когда шпонка устанавливается с затяжкой вдоль
Иногда шпоночные соединения разделяют на затяжные, когда шпонка устанавливается с затяжкой вдоль

Слайд 79НОРМИРОВАНИЕ ТОЧНОСТИ ЦИЛИНДРИЧЕСКИХ ЗУБЧАТЫХ КОЛЕС И ПЕРЕДАЧ
Зубчатое колесо представляет собой деталь
НОРМИРОВАНИЕ ТОЧНОСТИ ЦИЛИНДРИЧЕСКИХ ЗУБЧАТЫХ КОЛЕС И ПЕРЕДАЧ
Зубчатое колесо представляет собой деталь

Зубчатыми передачами называются механизмы, состоящие из зубчатых колес, которые сцепляются между собой и передают вращательное движение, обычно преобразуя угловые скорости и крутящие моменты.
Наибольшее распространение имеют цилиндрические зубчатые колеса и передачи, т.е. передачи с параллельными осями.
Принцип нормирования точности зубчатых колес и передач
Называются эти нормы:
нормы кинематической точности (3 – 12);
нормы плавности работы (3 – 12);
нормы контакта зубьев (Мгновенное пятно контакта, суммарное пятно контакта);
нормы бокового зазора (a, b, c, d, h, z, y, x).
Слайд 80Ряды точности (допуски) для зубчатых колес и передач по параметрам зацепления
При
Ряды точности (допуски) для зубчатых колес и передач по параметрам зацепления
При

Допуски" нормируется 12 степеней точности для зубчатых колес и передач.
Основным показателем бокового зазора в стандартах указывается гарантированный боковой зазор - это наименьший зазор, который получается при выполнении требований к колесу пары и обозначается jn min. При проектировании передач гарантированный зазор является исходным значением для выбора требований к параметрам колеса и передачи, определяющим этот зазор.
Для этих шести групп точности введены условные обозначения: H, E, D, C, B, A (Н - гарантированный зазор равен нулю, А - наибольший боковой зазор). Эти виды сопряжений - первый ряд (основной) точности для нормирования наименьшего (гарантированного) бокового зазора.
Установлено восемь видов допуска Tjn на боковой зазор, обозначенных буквами h, d, c, b, a, z, y, x в порядке возрастания допуска. Видам сопряжений Н и Е должен соответствовать вид допуска h, а видам сопряжений D, C, B и А - виды допусков d, c, b и а соответственно. Однако соответствие можно изменять и использовать виды допусков x, y, z, т.е. и эти ряды точности имеют рекомендательный характер. Эти нормы являются третьим рядом точности нормирования бокового зазора.
Слайд 81Схема расположения полей допусков Tjn для принятых видов сопряжений зубьев зубчатых колес
Схема расположения полей допусков Tjn для принятых видов сопряжений зубьев зубчатых колес
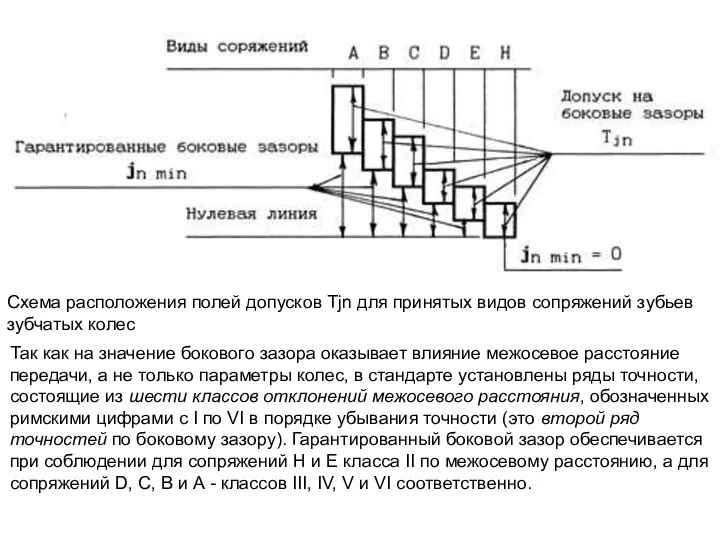
Так как на значение бокового зазора оказывает влияние межосевое расстояние передачи, а не только параметры колес, в стандарте установлены ряды точности, состоящие из шести классов отклонений межосевого расстояния, обозначенных римскими цифрами с I по VI в порядке убывания точности (это второй ряд точностей по боковому зазору). Гарантированный боковой зазор обеспечивается при соблюдении для сопряжений Н и Е класса II по межосевому расстоянию, а для сопряжений D, C, B и А - классов III, IV, V и VI соответственно.
Слайд 82Условные обозначения требований к точности зубчатых колес и передач
Таблица 11.1.
Чертежи
Условные обозначения требований к точности зубчатых колес и передач
Таблица 11.1.
Чертежи
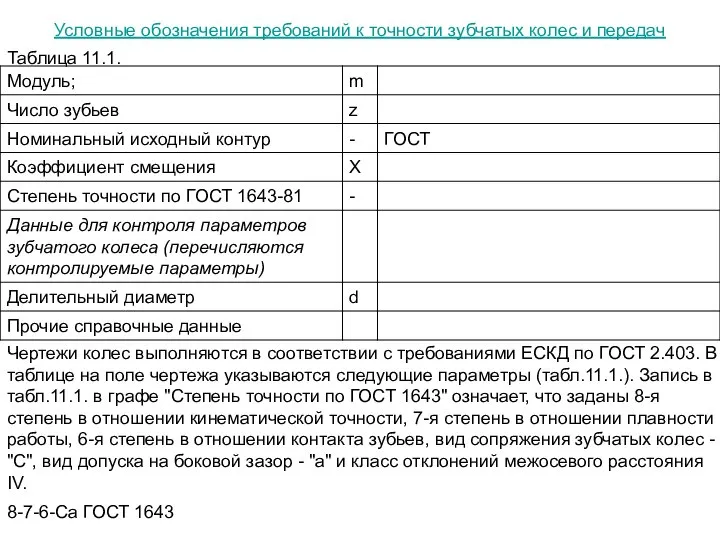
8-7-6-Са ГОСТ 1643
Слайд 83 Нормируемые параметры (показатели), характеризующие точность зубчатых колес и передач
Показатель кинематической точности
Кинематической
Нормируемые параметры (показатели), характеризующие точность зубчатых колес и передач
Показатель кинематической точности
Кинематической

Показатель плавности
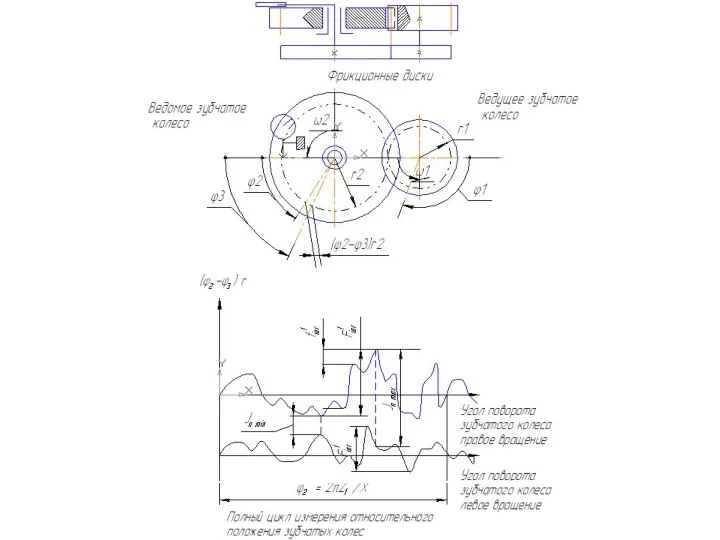
Местная кинематическая погрешность передачи (f 'ior) Наибольшая разность между местными соседними экстремальными значениями кинематической погрешности передачи за полный цикл измерения относительного положения зубчатых колес передачи
Показатель контакта зубьев
Мгновенное пятно контакта Часть активной боковой поверхности зуба колеса передачи, на которой располагаются следы его прилегания к зубьям шестерни, покрытым красителем, после поворота колеса на полный оборот
Показатель бокового зазора
Гарантированный боковой зазор J n min Наименьший предписанный боковой зазор
Слайд 84Таблица 11.2. Показатели кинематической точности (основные)
Таблица 11.2. Показатели кинематической точности (основные)

Слайд 86ОБЕСПЕЧЕНИЕ ТОЧНОСТИ РАЗМЕРНЫХ ЦЕПЕЙ
Взаимосвязь размеров элементов детали или отдельных деталей, входящих
ОБЕСПЕЧЕНИЕ ТОЧНОСТИ РАЗМЕРНЫХ ЦЕПЕЙ
Взаимосвязь размеров элементов детали или отдельных деталей, входящих

Размеры, образующие размерную цепь, называются составляющими звеньями, или просто звеньями, и обозначаются прописными русскими буквами с индексами (рис.6.1 - звенья А1,А2, А3).
Замыкающим звеном называется размер (звено), получаемый в размерной цепи последним при обработке или сборке.
Слайд 88Увеличивающим звеном размерной цепи называется звено, с увеличением которого размер замыкающего звена
Увеличивающим звеном размерной цепи называется звено, с увеличением которого размер замыкающего звена

Уменьшающим звеном размерной цепи называется звено, с увеличением которого замыкающее звено уменьшается. На рис.6.3 звенья А3, А4, А5, А6 являются уменьшающими звеньями.
Таким образом, обеспечение точности размерной цепи заключается в нормировании точности, т.е. указании предельных значений размеров всех звеньев цепи применительно к требованиям конструкции или технологического процесса.
Слайд 89Виды размерных цепей
Задачи, решаемые при обеспечении точности размерных цепей
Задача 1.
Виды размерных цепей
Задачи, решаемые при обеспечении точности размерных цепей
Задача 1.
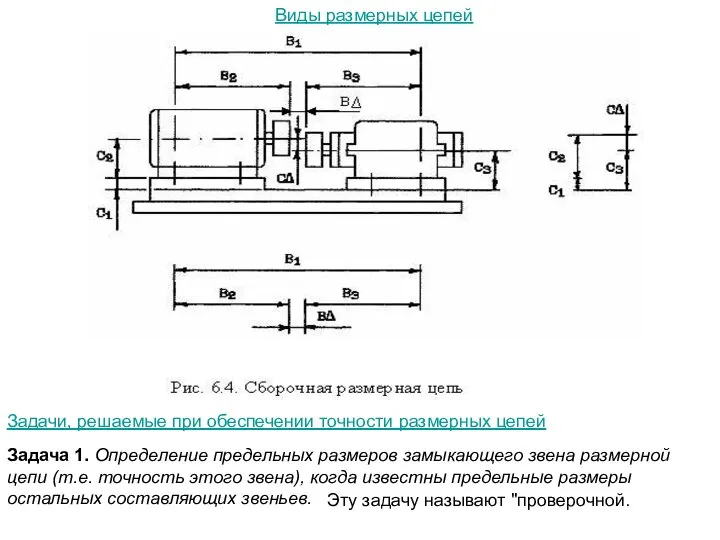
Эту задачу называют "проверочной.
Слайд 90Задача 2. Определение предельных размеров составляющих звеньев размерной цепи, когда известны предельные
Задача 2. Определение предельных размеров составляющих звеньев размерной цепи, когда известны предельные

Эту задачу называют "проектировочной", поскольку решать ее приходится при проектировании конструкции.
При решении этих двух задач (или иначе "решение размерной цепи") возможны два подхода. При одном подходе назначаются предельные значения всех звеньев, при которых обеспечивается полная взаимозаменяемость.
Метод называют расчетом на "максимум - минимум".
Расчет точности размерных цепей при обеспечении полной взаимозаменяемости (расчет на “максимум – минимум”)
При этом расчете необходимо нормировать точность размеров составляющих звеньев, чтобы точность замыкающего звена была обеспечена даже тогда, когда все размеры звеньев будут или максимально, или минимально допустимыми.
Задача 1 (проверочная). Известны предельные допустимые значения всех составляющих звеньев и требуется определить возможные предельные размеры замыкающего звена. Решение задачи осуществляется в следующей последовательности (рис.6.5).
1. Определяем номинальный размер замыкающего звена:
АΔ = (А1 + A2) - (А3 + А4),
т.е. АΔ = ΣАув - ΣАум.
Слайд 91Номинальный размер замыкающего звена равен сумме номинальных размеров увеличивающих звеньев (ΣАув) минус
Номинальный размер замыкающего звена равен сумме номинальных размеров увеличивающих звеньев (ΣАув) минус

2. Определение допуска замыкающего звена.
Из рис.6.5 определим:
АΔнб = А1нб + А2нб – А3нм – А4нм;
АΔнм = А1нм + А2нм – А3нб – А4нб.
Разность между наибольшим и наименьшим размерами замыкающего звена равна допуску на это звено, так же как и разность размеров составляющих звеньев:
(АΔнб - АΔнм) = (А1нб - А1нм) + (А2нб - А2нм) + (А3нм - А3нб) + (А4нм - А4нб)
или ТАΔ = ТА1 + ТА2 + ТА3 + ТА4,
Слайд 92
Допуск замыкающего звена равен сумме допусков составляющих звеньев. Отсюда следует, что
Допуск замыкающего звена равен сумме допусков составляющих звеньев. Отсюда следует, что

3. Определение предельных отклонений замыкающего звена
Из рис.6.5 может быть сделана запись с использованием понятий о верхнем и нижнем отклонениях составляющих звеньев:
где n - общее число увеличивающих звеньев; p - общее число уменьшающих звеньев. n + p = m –1.
Таким образом, выявлены все данные, необходимые для определения требований к точности замыкающего звена.
Слайд 93Пример. Определить номинальное, наибольшее и наименьшее значения и допуск замыкающего звена (размера
Пример. Определить номинальное, наибольшее и наименьшее значения и допуск замыкающего звена (размера
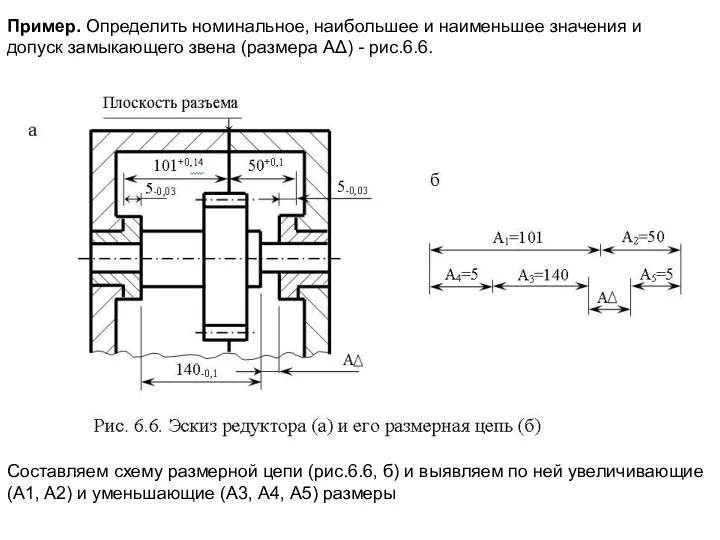
Составляем схему размерной цепи (рис.6.6, б) и выявляем по ней увеличивающие (A1, A2) и уменьшающие (А3, А4, A5) размеры
Слайд 94Определяем номинальное значение АΔ по формуле
АΔ = (А1 + A2) - (А3
Определяем номинальное значение АΔ по формуле АΔ = (А1 + A2) - (А3

Определяем допуск замыкающего звена по формулам АΔнб = (A1нб + А2нб) – (А3нм + А4нм + А5нм) = = (101,14 + 50,1) - (4,97 + 139,9 + 4,97) = 151,24 - 149,84 = 1,4 мм, АΔнм = (A1нм + A2нм) - (А3нб + А4нб + А5нб) = = (101,0 + 50,0) - (5,0 + 140,0 + 5,0) = 151,0 - 149,0 = 1,0 мм, ТАΔ = (АΔнб - АΔнм) = 1,4 – 1,0 = 0,4 мм, или второй вариант ТАΔ = (АΔнб - АΔнм) = (A1нб - A1нм) + (A2нб – A2нм) + (A3нб – A3нм) + (A4нб – A4нм) + (A5нб – A5нм) =(101,14 - 101,0) + (50,1 - 50,0) + (5,0 - 4,97) + (140,0 - 139,9) + (5,0 - 4,97) = 0,14 + 0,1 + 0,03 + 0,1 + 0,03 = 0,4 мм.
Определяем предельные отклонения замыкающего звена: верхнее отклонение (замыкающее звено отверстие) (ES) AΔ = [(ES)A1+ (ES)A2] - [(еi)А3+ (еi)А4 + (ei)A5] = [0,14 + 0,1] - [- 0,03 + (-0,1) + (-0,03)] = +0, 4 мм; нижнее отклонение (ЕI)АΔ = [(EI)A11+ (EI)A2] - [(еs)А3+ (es)A4+ (es)A5] = [0 + 0] - [0 + 0 + 0] = 0.
Таким образом, при заданных номинальных размерах и предельных отклонениях составляющих размеров замыкающий размер должен быть выполнен с верхним предельным отклонением 0,4 мм и нижним 0, т.е. АΔ = 1+0,4 мм.
Слайд 95Пример. Определить допуски составляющих размеров деталей сборочной единицы, показанной на рис.6.6. Схема
Пример. Определить допуски составляющих размеров деталей сборочной единицы, показанной на рис.6.6. Схема

Заданы номинальные значения составляющих размеров цепи и предельные отклонения исходного размера АΔмакс = 1,75 мм; АΔмин = 1 мм.
Находим номинальный размер исходного звена по формуле
АΔ = (A1 + A2) - (A3 + А4 + A5) = (101 + 50) - (5 + 140 +5) = 1 мм.
Наименьший предельный размер совпадает с номинальным, поэтому АΔ = 1+0,75, а допуск замыкающего звена равен ТАΔ = 0,75 мм.
Среднее число единиц допуска в размерной цепи определяем по формуле
 Данное видео посвещается автобусу Икарус 256, ушедшему с дорог Кирова
Данное видео посвещается автобусу Икарус 256, ушедшему с дорог Кирова Три состояния вещества. Различие в молекулярном строении твердых тел, жидкостей и газов
Три состояния вещества. Различие в молекулярном строении твердых тел, жидкостей и газов Osnovy_AU
Osnovy_AU Молекулярная физика. Основные положения молекулярно-кинетической теории
Молекулярная физика. Основные положения молекулярно-кинетической теории Идеальный газ
Идеальный газ Время и его измерение. Основы кинематики
Время и его измерение. Основы кинематики Урок 9п
Урок 9п Технологический расчет комплекса технического обслуживания с разработкой проекта зоны
Технологический расчет комплекса технического обслуживания с разработкой проекта зоны Лист лотоса. Оптические и СЗМ изображения
Лист лотоса. Оптические и СЗМ изображения Реактивное движение
Реактивное движение Рентгеновские трубки (РТ). Классификация. Обозначение. Основные характеристики. (Лекция 4)
Рентгеновские трубки (РТ). Классификация. Обозначение. Основные характеристики. (Лекция 4) Спектрометрия ультрафиолетовой и видимой части спектра
Спектрометрия ультрафиолетовой и видимой части спектра Эволюция физики в видеоиграх
Эволюция физики в видеоиграх Safarov_Krasnov
Safarov_Krasnov Что за знаки перед нами?
Что за знаки перед нами? Повышение КПД ГТУ путём внедрения регенеративного цикла
Повышение КПД ГТУ путём внедрения регенеративного цикла Инфракрасное излучение
Инфракрасное излучение Телескопы
Телескопы 7_Sily_v_prirode_sila_tyazhesti_ves (1)
7_Sily_v_prirode_sila_tyazhesti_ves (1) Типы линз. Формула линзы. Применение насадочных линз в фотографии
Типы линз. Формула линзы. Применение насадочных линз в фотографии Презентация на тему: Физика в современном театре
Презентация на тему: Физика в современном театре Поперечная дифференциальная токовая защита. Выключатели с одной стороны линий
Поперечная дифференциальная токовая защита. Выключатели с одной стороны линий Электрический ток в газах
Электрический ток в газах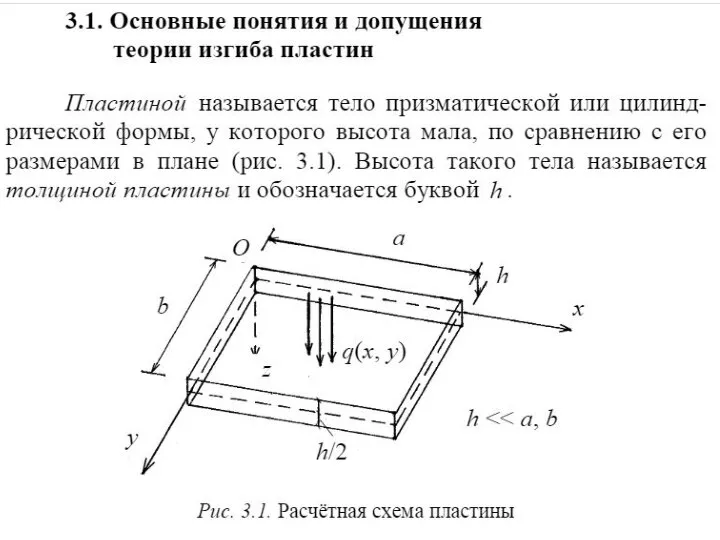 Основные понятия и допущения теории и изгиба пластин
Основные понятия и допущения теории и изгиба пластин Защитное зануление
Защитное зануление Презентация на тему Изменение агрегатного состояния вещества
Презентация на тему Изменение агрегатного состояния вещества  Вес. Невесомость. Перегрузки
Вес. Невесомость. Перегрузки Пеленгация РЭC
Пеленгация РЭC