Принцип Даламбера для материальной точки. Лекция 2

Сила , равная по модулю произведению массы точки на ее ускорение и направленная в сторону, противоположную ускорению, называется силой инерции (даламберовой силой).

Если в каждый данный момент к действующим на точку активным силам и силам реакции связей прибавить силу инерции, то полученная система сил будет находиться в равновесии и по отношению к ней будут справедливы все уравнения статики.
Принцип Даламбера для точки
Значение принципа Даламбера состоит в том, что он позволяет при решении динамических задач составлять уравнения движения в форме уравнений равновесия.

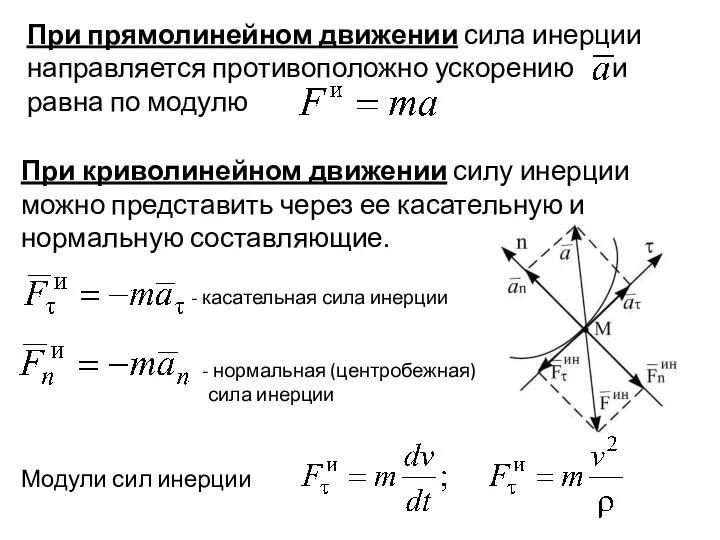
- касательная сила инерции
нормальная (центробежная)
сила инерции
Модули сил инерции
При криволинейном движении силу инерции можно представить через ее касательную и нормальную составляющие.
При прямолинейном движении сила инерции направляется противоположно ускорению и равна по модулю

Принцип Даламбера для
механической системы

Если в любой момент времени к каждой из точек системы, кроме действующих на нее внешних и внутренних сил, приложить соответствующие силы инерции, то полученная система сил будет находиться в равновесии и к ней можно будет применять все уравнения статики.
Принцип Даламбера для системы:

геометрическая сумма сил, находящихся в равновесии, и сумма их моментов относительно любого центра О равны нулю
Тогда на основании принципа Даламбера:
Введем обозначения:
Главный вектор сил инерции
Главный момент сил инерции относительно центра О.

Главный вектор и главный момент сил инерции твердого тела.

Главный вектор сил инерции тела, совершающего любое движение, равен произведению массы тела на ускорение его центра масс и направлен противоположно этому ускорению.
– масса тела;
– ускорение центра масс тела.
где

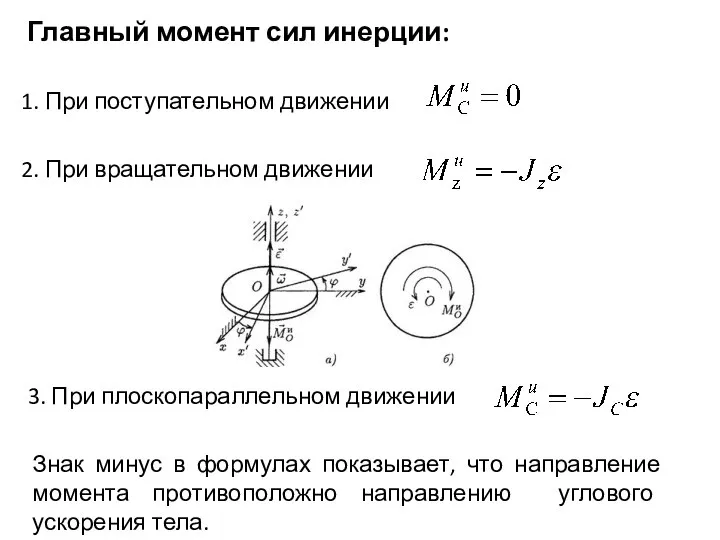
Главный момент сил инерции:
1. При поступательном движении
2. При вращательном движении
3. При плоскопараллельном движении
Знак минус в формулах показывает, что направление момента противоположно направлению углового ускорения тела.