Электромагнитные колебания и волны

Волна - это процесс распространения колебаний в пространстве с течением времени

Классификации волн
В зависимости от физической среды, в которой распространяются волны, их свойства различны и поэтому различают:
Электромагнитные волны (радиоволны, свет, рентгеновские лучи);
Упругие волны (звук, сейсмические волны);
Волны в плазме;
Гравитационные волны;
Объёмные волны (распространяющиеся в толще среды);
Волны на поверхности жидкости.

Виды волн
Продольные волны (волны сжатия) — волна распространяется параллельно колебаниям частиц среды (звук);
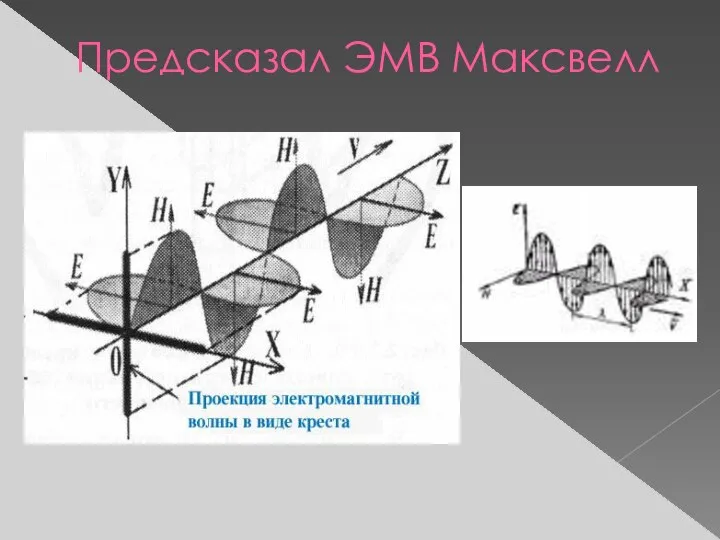
Поперечные волны (волны сдвига) — частицы среды колеблются перпендикулярно направлению распространения волны (электромагнитные волны, волны на поверхностях разделения сред);

Виды волн
Продольные-плоская Поперечные

Виды волн
Продольная Поперечная сферическая сферическая

Характеристики волны
временная периодичность — скорость изменения фазы с течением времени в какой-то заданной точке, называемую частотой волны f ; период Т
пространственная периодичность — скорость изменения фазы в определённый момент времени с изменением координаты — длина волны λ

Интенсивность волны
О силе волны судят по её амплитудеО силе волны судят по её амплитуде. В отличии от колебания амплитуда волны — векторная величина.
Но для количественной характеристике переносимой волной энергии используется вектор плотности потока энергии I. Его направление совпадает с направлением переноса энергии, а абсолютная величина равна количеству энергии, переносимой волной за единицу времени через единичную площадку, перпендикулярную направлению вектора. При небольших амплитудах: I=kAA
где A — амплитуда; k — коэффициент пропорциональности, зависящий от природы волны и свойств среды, где эта волна распространяется

Предсказал ЭМВ Максвелл

Открыл ЭМВ Герц

Применение ЭМВ

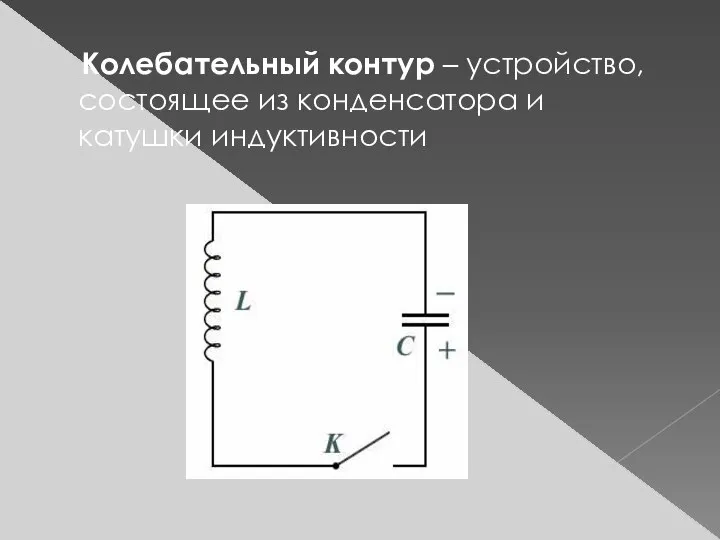
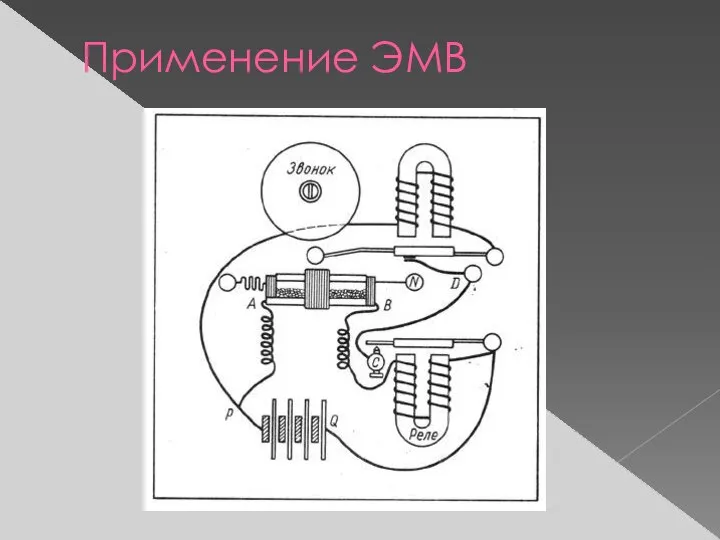
Колебательный контур – устройство, состоящее из конденсатора и катушки индуктивности

Колебания физических величин, характеризующих электромагнитные взаимодействия, называют электромагнитными колебаниями.
Как известно из математики, если функция y(t) удовлетворяет условию:
где В, С, D – числовые множители, не зависящие от времени, то y(t) – гармоническая функция следующего вида:
y(t) = A cos (wt + j0),
причем , а значения А и j0 определяются исходя из начальных условий.
Это позволяет получить уравнение гармонических колебаний в колебательном контуре из закона сохранения энергии.

Для произвольного момента времени, когда заряд на конденсаторе равен q(t), а ток в цепи равен I(t), закон сохранения энергии приобретает следующий вид:
где q0 – заряд на конденсаторе в начальный момент времени. Учитывая, что , можно утверждать, что это уравнение имеет вид
и аналогично уравнению, где роль меняющейся во времени величины играет заряд: y(t) = q(t).
Тогда решением данного уравнения является функция
q(t) = q0 cos (wt + j0),
где , т.е. изменение заряда в колебательном контуре происходит по гармоническому закону. Значение j0 определяется из начальных условий; в частности, если в начальный момент времени q(0) = q0, то j0 = 0.