Содержание
- 2. 3.1. Приведение произвольной плоской системы сил к простейшему виду
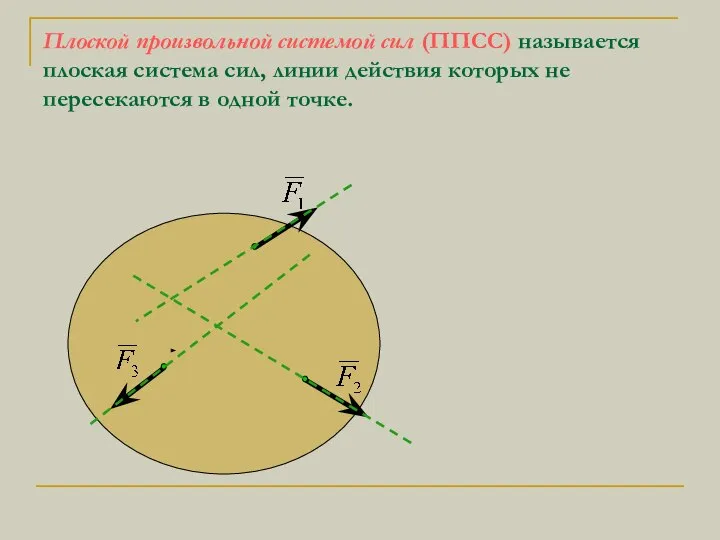
- 3. Плоской произвольной системой сил (ППСС) называется плоская система сил, линии действия которых не пересекаются в одной
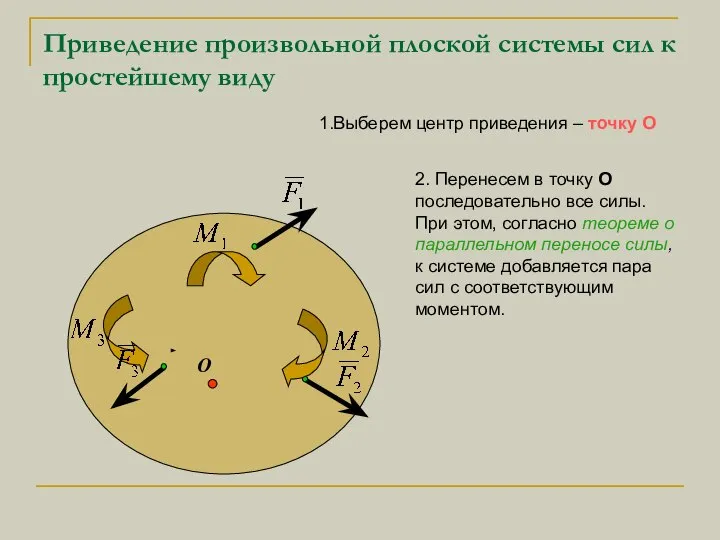
- 4. Приведение произвольной плоской системы сил к простейшему виду 1.Выберем центр приведения – точку О О 2.
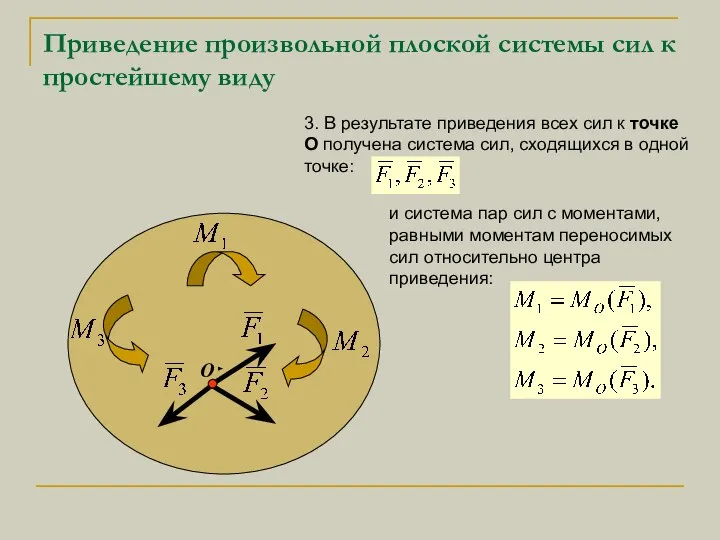
- 5. Приведение произвольной плоской системы сил к простейшему виду 3. В результате приведения всех сил к точке
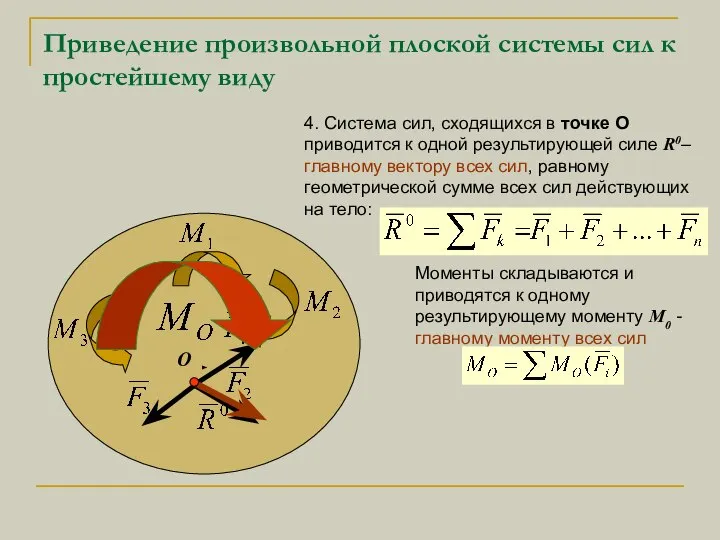
- 6. Приведение произвольной плоской системы сил к простейшему виду 4. Система сил, сходящихся в точке О приводится
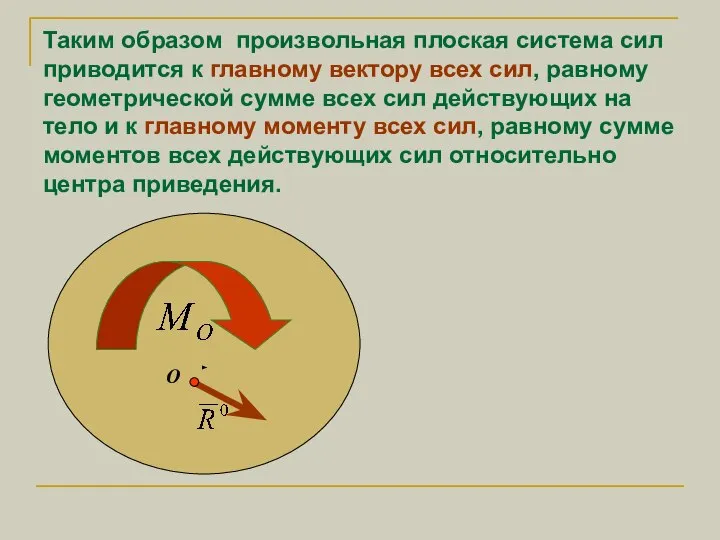
- 7. Таким образом произвольная плоская система сил приводится к главному вектору всех сил, равному геометрической сумме всех
- 8. 3.2. Условия равновесия произвольной плоской системы сил
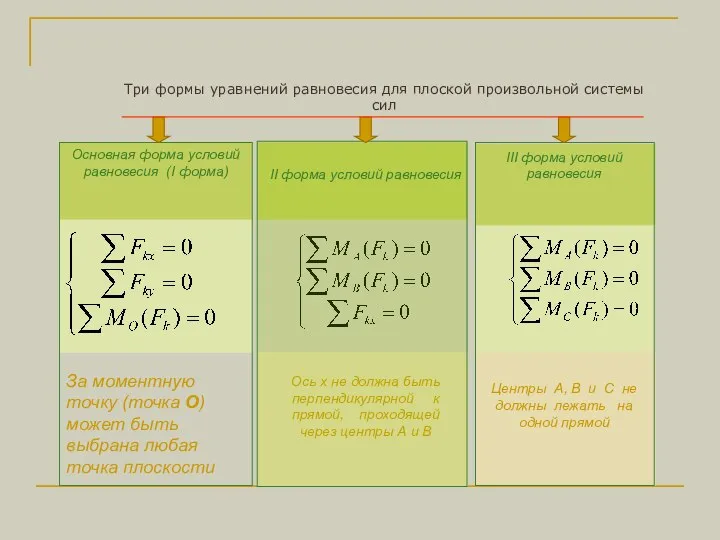
- 9. Условия равновесия произвольной плоской системы сил Необходимым и достаточным условием равновесия плоской системы сил являются равенство
- 10. Ось х не должна быть перпендикулярной к прямой, проходящей через центры А и В Центры А,
- 11. - уравнение проекций всех сил на ось х - уравнение проекций всех сил на ось у
- 12. Важно ! Для одного твердого тела можно составить только три (!) независимых уравнения равновесия по одной
- 13. Важно ! В задаче на равновесие одного твердого тела может быть только три неизвестные силы (обычно
- 14. 3.3. Виды сил, действующих на тело
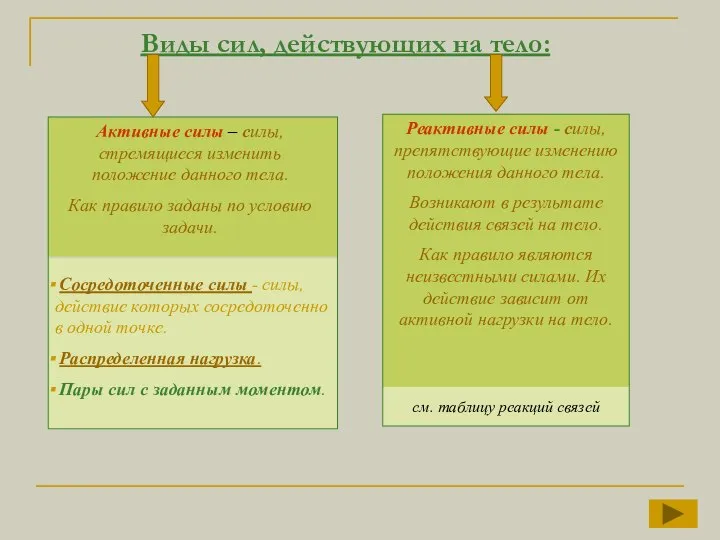
- 15. Виды сил, действующих на тело: см. таблицу реакций связей Активные силы – силы, стремящиеся изменить положение
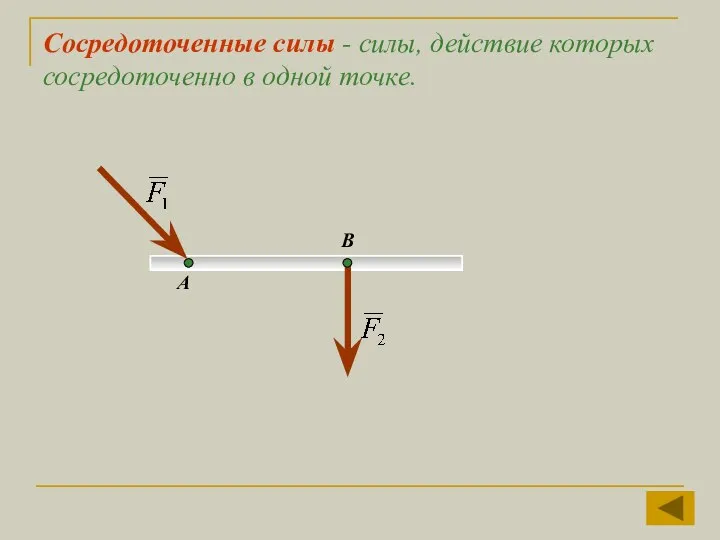
- 16. Сосредоточенные силы - силы, действие которых сосредоточенно в одной точке. А В
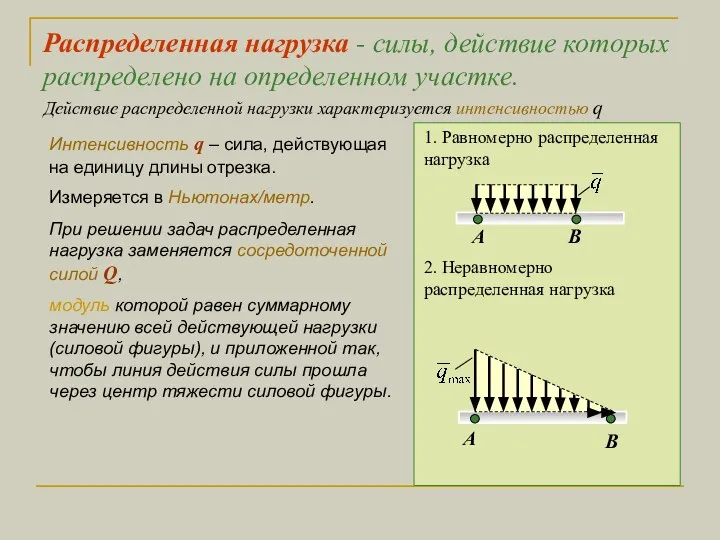
- 17. Распределенная нагрузка - силы, действие которых распределено на определенном участке. Действие распределенной нагрузки характеризуется интенсивностью q
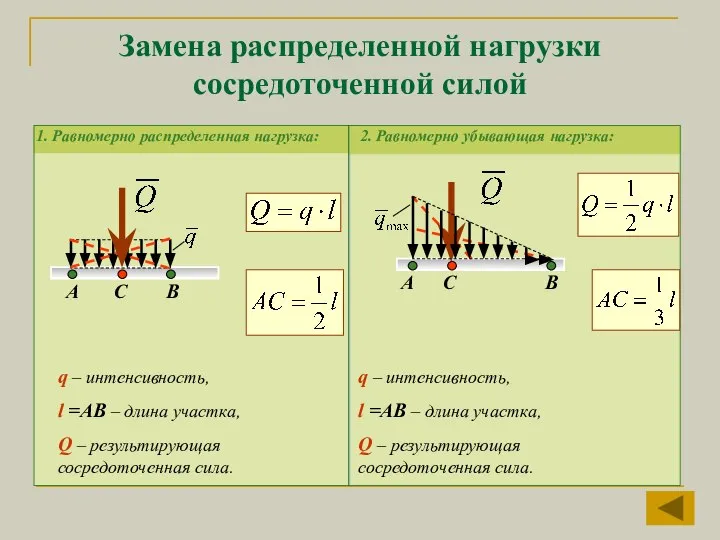
- 18. Замена распределенной нагрузки сосредоточенной силой 1. Равномерно распределенная нагрузка: А В С 2. Равномерно убывающая нагрузка:
- 20. Скачать презентацию







 Проект Радиация
Проект Радиация Последовательное соединение
Последовательное соединение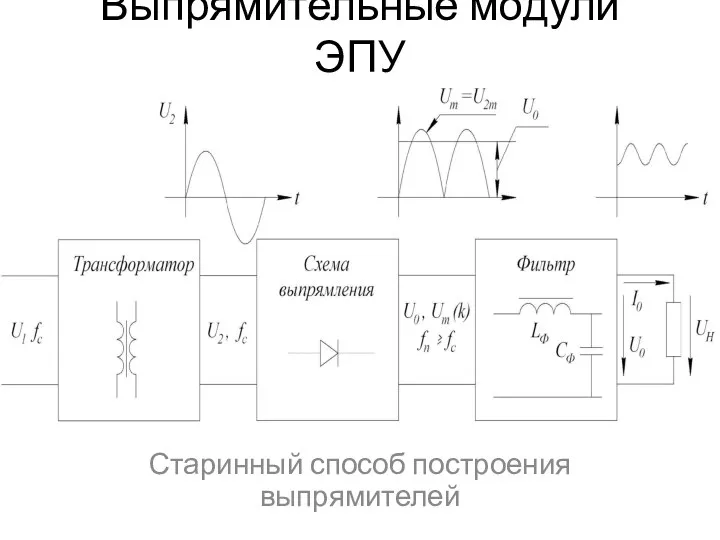 Выпрямительные модули ЭПУ
Выпрямительные модули ЭПУ Многоповерхностная теория пластичности с одной активной поверхностью
Многоповерхностная теория пластичности с одной активной поверхностью Динамика. Первый закон Ньютона
Динамика. Первый закон Ньютона Электрический ток в электролитах. Урок 4
Электрический ток в электролитах. Урок 4 Модель атома Томсона
Модель атома Томсона Метрология. МНК. Результаты измерений
Метрология. МНК. Результаты измерений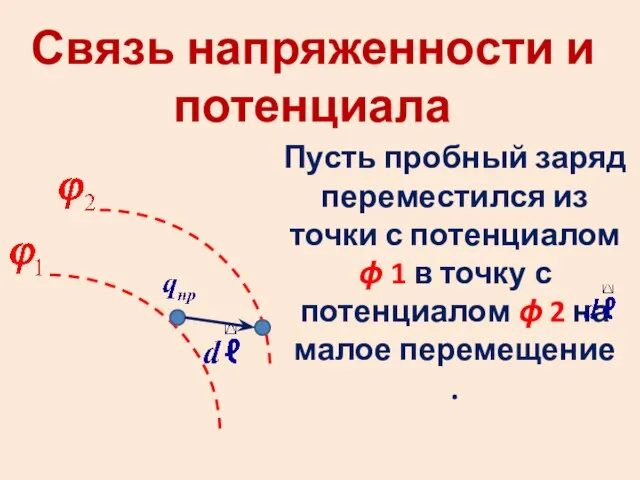 Связь напряженности и потенциала
Связь напряженности и потенциала Магнитное поле тока
Магнитное поле тока Магнитопорошковая дефектоскопия (МПД)
Магнитопорошковая дефектоскопия (МПД) Фундаментальные физические величины. Упражнения. Часть 2
Фундаментальные физические величины. Упражнения. Часть 2 Техника высоких напряжений
Техника высоких напряжений Парогенератор. Оболочка ТВЕЛа
Парогенератор. Оболочка ТВЕЛа Самоиндукция. Индуктивность
Самоиндукция. Индуктивность Приближенное подобие и моделирование
Приближенное подобие и моделирование Строение атома. Состав атомных ядер. Изотопы. (8 класс)
Строение атома. Состав атомных ядер. Изотопы. (8 класс) Микронометр
Микронометр Состав атомного ядра
Состав атомного ядра Электронные фильтры
Электронные фильтры Всемирное тяготение
Всемирное тяготение Кипение воды
Кипение воды Внутренняя энергия
Внутренняя энергия Энергия. Потенциальная и кинетическая энергия. Закон сохранения энергии
Энергия. Потенциальная и кинетическая энергия. Закон сохранения энергии Явление электромагнитной индукции
Явление электромагнитной индукции Мощность как физическая величина
Мощность как физическая величина Семинар 15. Изгибные колебания стержня (самостоятельная)
Семинар 15. Изгибные колебания стержня (самостоятельная) Интерференция и дифракция световых волн
Интерференция и дифракция световых волн