Дифракция. Дифракционная решетка

Содержание
Дифракция волн
Наблюдение дифракции волн
Объяснение дифракции волн
Дифракция волн в природе
Дифракция света
Наблюдение дифракции света
Зоны Френеля
Дифракция света в природе
Дифракционная решетка
Ключевые задачи
Рисунки в задачах
Почему «0» max белый
Максимальный порядок спектра

Многообразие оптических явлений делает окружающий мир загадочным и потрясающе красивым. Явления, подтверждающие волновую природу света, – интерференция и дифракция.

Явление огибания механическими волнами преград наблюдается когда речные волны свободно огибают выступающие из воды предметы и распространяются так, как будто этих предметов не было совсем.
Явление, свойственное всем волновым процессам.
Звуковые волны так же огибают препятствия и мы можем слышать сигнал автомобиля за углом дома, когда самого автомобиля не видно.

В середине 17-го века итальянский ученый
Ф. Гримальди наблюдал странные тени от небольших предметов, помещенных в узкий пучок света. Эти тени не имели четких границ, были окаймлены цветными полосами.

Томас Юнг
(13.06.1773-10.05.1829)

Христиан Гюйгенса
(14.04.1629 - 8.07.1695) :
В становлении представлений о том, что распространение света является волновым процессом, большую роль сыграл Христиан Гюйгенс.

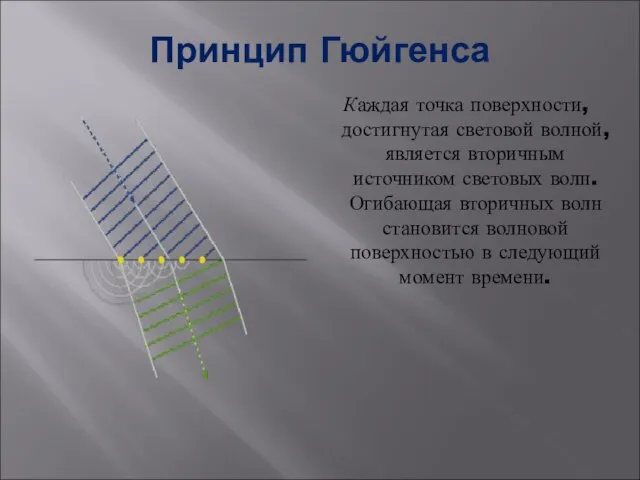
Принцип Гюйгенса
Каждая точка поверхности, достигнутая световой волной, является вторичным источником световых волн. Огибающая вторичных волн становится волновой поверхностью в следующий момент времени.

Зависимость отклонения волн от размеров отверстия
Дифракция Волн - явление огибания волнами препятствий и проникновение их в область геометрической тени.
Наблюдение дифракции волн
Далее

Дифракция света – огибание световой волной непрозрачных тел с проникновением в область геометрической тени и образованием там интерференционной картины.

Качественное объяснение дифракции
Волны огибают большую скалу и область тени постепенно исчезает
По принципу Гюйгенса-Френеля огибающая вторичных волн на краях препятствия заходит в область тени.
Далее

Френель Огюстен Жан
(10.05.1788–14.06.1827).
Огюстен Френель заложил основы волновой оптики, дополнив принцип Гюйгенса идеей интерференции вторичных волн: он построил количественную теорию дифракции.

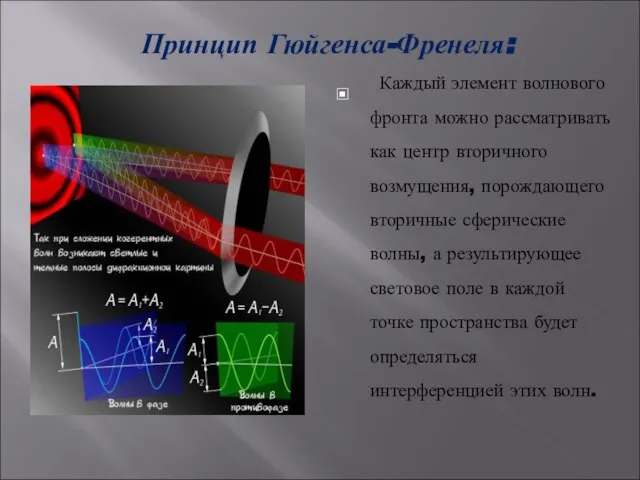
Принцип Гюйгенса-Френеля:
Каждый элемент волнового фронта можно рассматривать как центр вторичного возмущения, порождающего вторичные сферические волны, а результирующее световое поле в каждой точке пространства будет определяться интерференцией этих волн.

Качественное объяснение дифракции света
Модель дифракции
здесь
Огюстен Жан Френель в 1818 году предложил разбить волновую поверхность на отдельные зоны так, чтобы волны от ближайших зон шли в противофазе. При трех открытых зонах в центре экрана светлое пятно, т.к. для 1 и 2 зоны выполняется условие min, а третья создает светлое пятно.
Далее

Наблюдение дифракции света

Дифракционная картина, возникающей на экране при дифракции света на линейном препятствии (щель)

Модель дифракционной картины, возникающей на экране при дифракции света на линейном препятствии (щель), при различных длинах волн падающего света.

Модель дифракционной картины, возникающей на экране при дифракции света на круглом препятствии (шарик), при различных длинах волн падающего света и размерах препятствия.

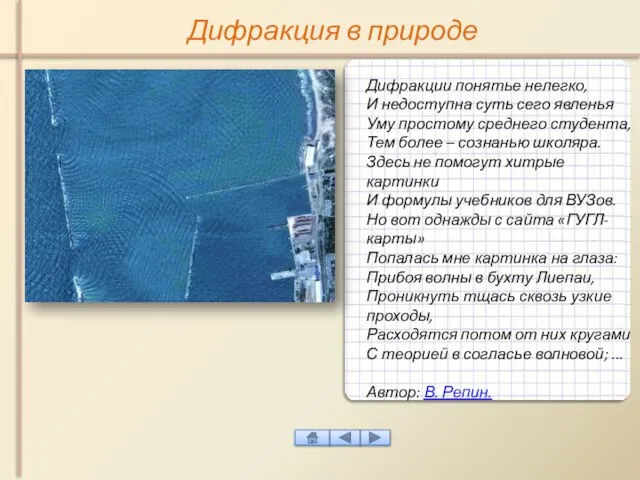
Дифракция в природе
Гло́рия (лат. gloria — украшение; ореол) — оптическое явление в облаках.
Наблюдается на облаках, расположенных прямо напротив источника света. Наблюдатель должен находиться на горе или на самолёте, а источник света (Солнце или Луна) — за его спиной. Глория объясняется дифракцией света, ранее уже отражённого в капельках облака так, что он возвращается от облака в том же направлении, по которому падал, то есть к наблюдателю.
В Китае глорию называют «светом Будды». Первые письменные свидетельства о наблюдении явления с горы Эмэйшань датируются 63 г. н. э. Цветное гало всегда окружает тень наблюдателя, что часто толковалось как степень его просветления (приближённости к Будде и другим божествам).
Википедия.
Далее

Дифракция в природе
Дифракции понятье нелегко,
И недоступна суть сего явленья
Уму простому среднего студента,
Тем более – сознанью школяра.
Здесь не помогут хитрые картинки
И формулы учебников для ВУЗов.
Но вот однажды с сайта «ГУГЛ-карты»
Попалась мне картинка на глаза:
Прибоя волны в бухту Лиепаи,
Проникнуть тщась сквозь узкие проходы,
Расходятся потом от них кругами
С теорией в согласье волновой; ...
Автор: В. Репин.

Лунные венцы.

Границы применимости геометрической оптики.
Наиболее отчетливо дифракция света проявляется тогда, когда выполняется данное условие (условие наблюдения дифракции).
Где D- размер препятствия или отверстия, λ- длина световой волны, L- расстояние от препятствия до места, где наблюдается дифракционная картина.

Разрешающая способность оптических приборов.
Дифракция налагает также предел на разрешающую способность телескопа. Предельное угловое расстояние(δ) между светящимися точками, при котором их можно различать, определяется отношением длины волны(λ) к диаметру объектива (D).

Дифракцию света используют для создания чувствительных спектральных приборов.
Дифракционные явления приносят не только пользу,
но и вред, ограничивая разрешающую способность оптических приборов.

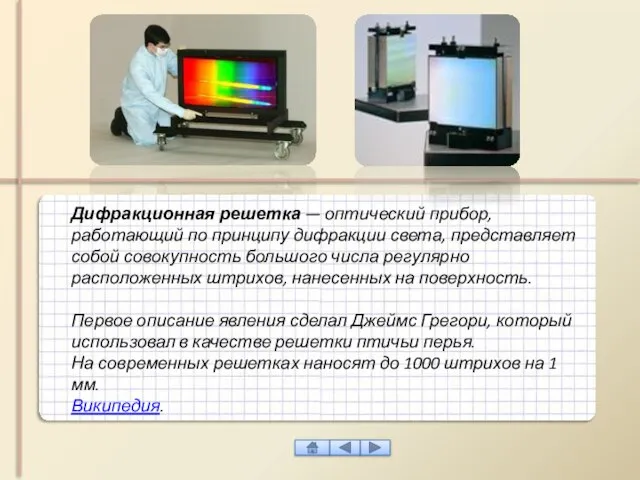
Дифракционная решетка — оптический прибор, работающий по принципу дифракции света, представляет собой совокупность большого числа регулярно расположенных штрихов, нанесенных на поверхность.
Первое описание явления сделал Джеймс Грегори, который использовал в качестве решетки птичьи перья.
На современных решетках наносят до 1000 штрихов на 1 мм.
Википедия.

ДИФРАКЦИОННАЯ РЕШЕТКА
– оптический прибор, представляющий собой совокупность большого числа регулярно расположенных штрихов (щелей, выступов),
нанесенных на некоторую поверхность
(от 0,25 до 6000
штрихов на 1 мм).

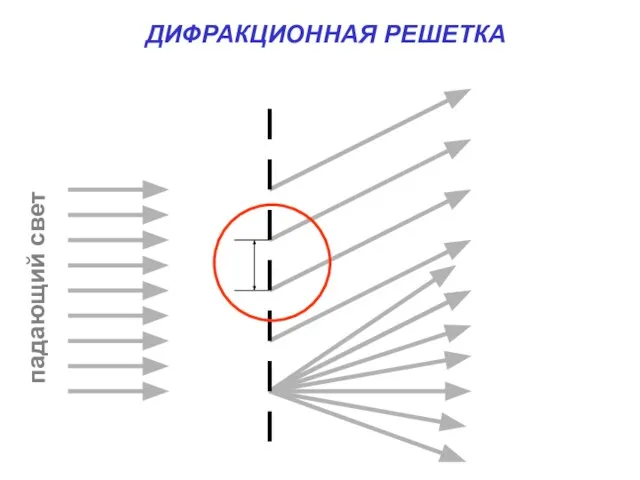
ДИФРАКЦИОННАЯ РЕШЕТКА

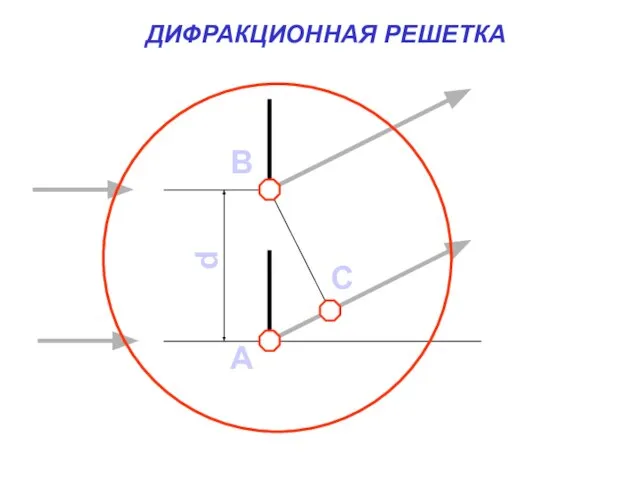
d
B
A
C
ДИФРАКЦИОННАЯ РЕШЕТКА

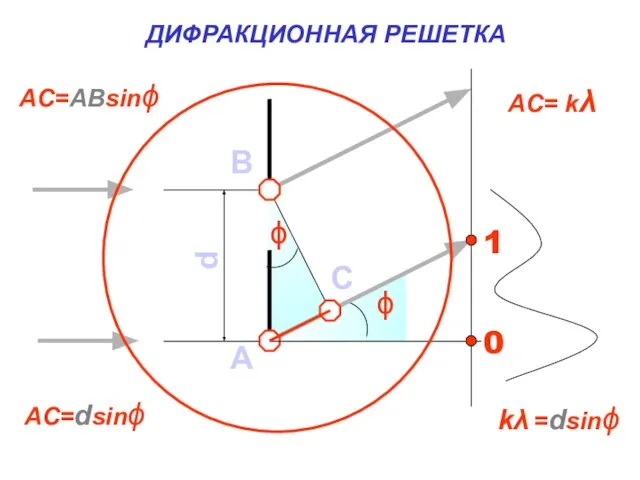
d
B
A
C
ϕ
ϕ
AC=ABsinϕ
AC= kλ
AC=dsinϕ
kλ =dsinϕ
ДИФРАКЦИОННАЯ РЕШЕТКА

В упрощенной теории каждую прозрачную часть можно считать точечным источником света, который излучает вторичные волны по всем направлениям.
Разность хода между волнами от ближайших источников зависит от выбранного направления.
Чем больше угол отклонения, тем больше разность хода.
Принцип действия дифракционной решетки

Величина, равная сумме ширины прозрачной и непрозрачной части, называется постоянной дифракционной решетки (d).
Из прямоугольного треугольника:
Для некоторых углов разность хода кратна длине волны, следовательно, для этих углов выполняется условие max:
Принцип действия дифракционной решетки
Далее

d sinϕ = kλ
d – период решетки
- длина световой волны
k = 0,1,2,3…- максимумы
ϕ - угол на соответствующий максимум
ДИФРАКЦИОННАЯ РЕШЕТКА

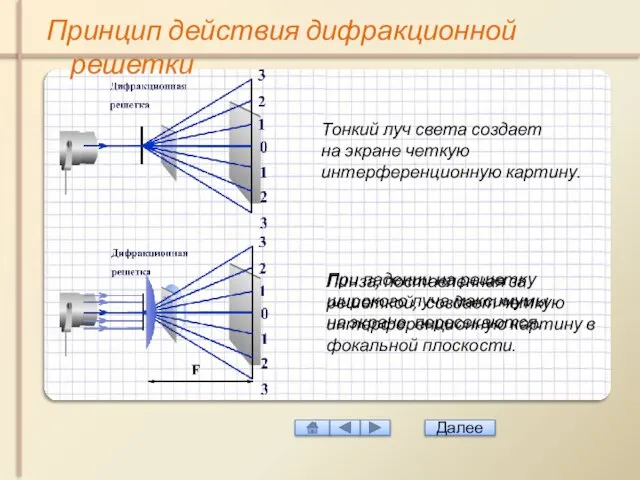
Тонкий луч света создает
на экране четкую
интерференционную картину.
При падении на решетку широкого луча максимумы на экране пересекаются.
Линза, поставленная за решеткой, создает четкую интерференционную картину в фокальной плоскости.
Принцип действия дифракционной решетки
Далее

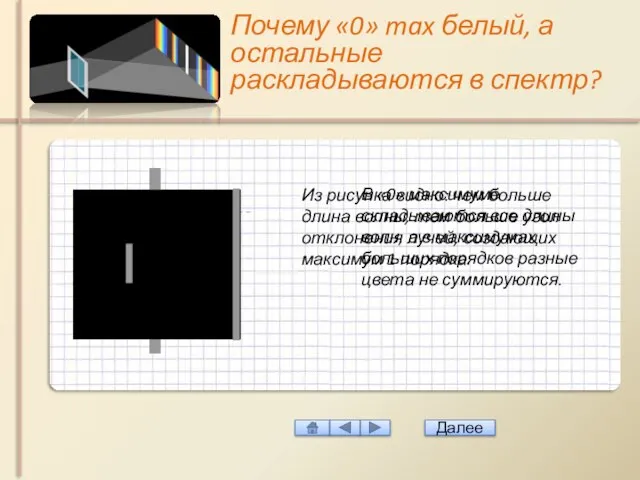
Почему «0» max белый, а остальные раскладываются в спектр?
Из рисунка видно: чем больше длина волны, тем больше угол отклонения лучей, создающих максимум 1 порядка.
В «0» максимуме складываются все длины волн, а в максимумах больших порядков разные цвета не суммируются.
Далее

И
И
Почему решетки не создают спектры любого порядка?
Из формулы дифракционной решетки выражаем порядок спектра:
Поскольку sinφ ≤ 1, то
Аналитическое решение
1. Из рисунка видно, что максимальная разность хода не превышает период решетки Δd ≤ d
Графическое решение
2. Применяя условие максимума Δd = kλ, получаем:
Далее

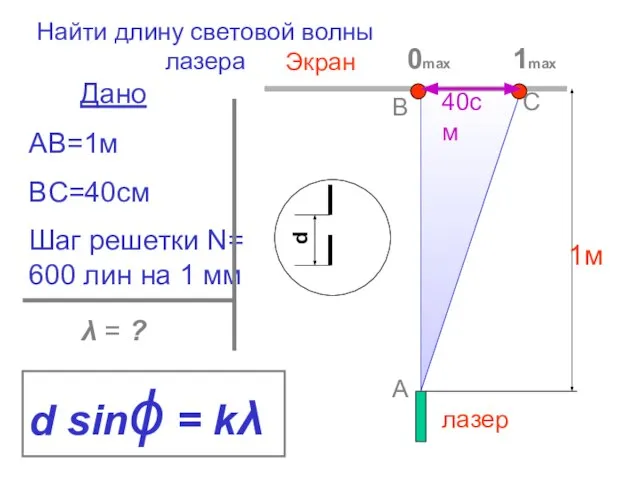
Дано
AB=1м
BC=40см
Шаг решетки N=
600 лин на 1 мм
λ = ?
d sinϕ = kλ
Найти длину световой волны лазера

задача
На дифракционную решетку имеющую 500 штрихов на 1 мм падает плоская монохроматическая волна длиной λ= 500 нм.
Определите угол направления на 2 максимум.
Определите наибольший порядок спектра k, который можно наблюдать с данной решеткой.

ход решения задачи
d sinϕ = kλ λ= 500 нм = 500*10-9м найдем d
1мм = 0,001м
0,001м/500 = 0,000 002 м = 2*10-6м
Найдем угол ϕ
sinϕ = kλ /d
sinϕ = 2 * 500*10-9м/ 2*10-6м = 0,5
sinϕ = 0,5
∠ϕ = 30°
Найдем наибольший порядок спектра k
максимальному k соответствует sinϕ =1 ⇒ k =d/λ = 4