Содержание
- 2. Механическая работа – скалярная величина, характеризующая действие силы на некотором участке пути; [A]=Дж.
- 3. Формулы (3.1) справедливы при вычислении работы в случае когда, тело движется по прямолинейной траектории, а сила,
- 4. Мощность - скалярная величина, характеризующая быстроту совершения работы; [P]=Вт. Средняя мощность: (3.4) Мгновенная мощность: (3.5)
- 5. Понятие работы тесно связано с понятием энергии, так как совершение работы всегда сопровождается изменением энергии. Энергия
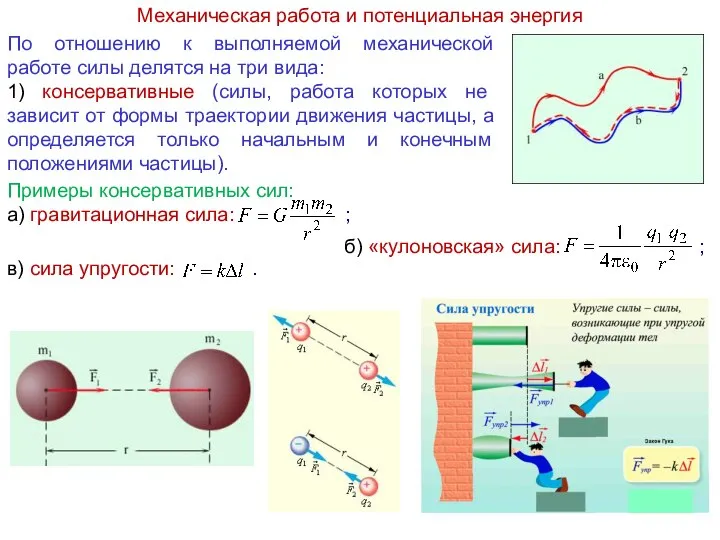
- 6. Механическая работа и потенциальная энергия Примеры консервативных сил: а) гравитационная сила: ; в) сила упругости: .
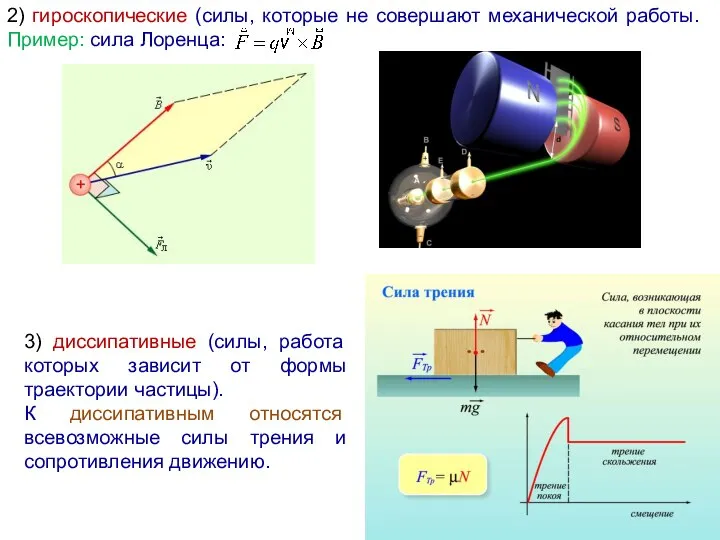
- 7. 2) гироскопические (силы, которые не совершают механической работы. Пример: сила Лоренца: 3) диссипативные (силы, работа которых
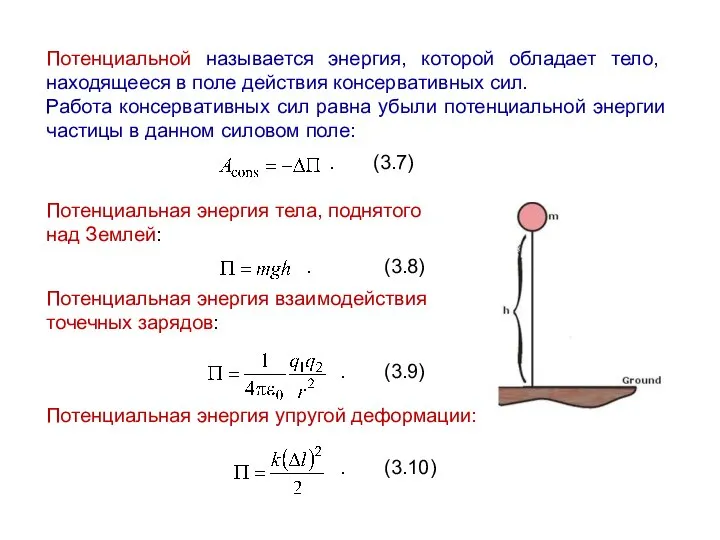
- 8. Потенциальной называется энергия, которой обладает тело, находящееся в поле действия консервативных сил. Работа консервативных сил равна
- 10. Скачать презентацию
![Механическая работа – скалярная величина, характеризующая действие силы на некотором участке пути; [A]=Дж.](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1028787/slide-1.jpg)

![Мощность - скалярная величина, характеризующая быстроту совершения работы; [P]=Вт. Средняя мощность: (3.4) Мгновенная мощность: (3.5)](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1028787/slide-3.jpg)

 Порядок осмотра, выявления неисправностей
Порядок осмотра, выявления неисправностей Физические величины и их измерения. Урок 2. 7 класс
Физические величины и их измерения. Урок 2. 7 класс Надежность
Надежность Кинематика вращательного движения
Кинематика вращательного движения Квантовая физика, часть1
Квантовая физика, часть1 Поверхностное натяжение
Поверхностное натяжение Определение массы небесных тел
Определение массы небесных тел Уход за швейной машиной
Уход за швейной машиной авторы: Маньков Данил И пономарёв глеб Электромагнитные явления
авторы: Маньков Данил И пономарёв глеб Электромагнитные явления 693034 (2)
693034 (2) Устройство и работа ДВС (двигателя внутреннего сгорания)
Устройство и работа ДВС (двигателя внутреннего сгорания) Прямолинейное равноускоренное движение
Прямолинейное равноускоренное движение Сила Ампера
Сила Ампера Стоячие волны Урок физики в 10 классе (естественно-научный профиль) © Автор Богданова Ирина Викторовна
Стоячие волны Урок физики в 10 классе (естественно-научный профиль) © Автор Богданова Ирина Викторовна Средства связи: принцип действия, виды, назначение
Средства связи: принцип действия, виды, назначение Физические основы микроэлектроники. Радиоматериалы и радиокомпоненты
Физические основы микроэлектроники. Радиоматериалы и радиокомпоненты Сравнительная характеристика проводниковых материалов. Медь и алюминий
Сравнительная характеристика проводниковых материалов. Медь и алюминий Экспериментальное исследование влияния несинусоидальности напряжения на работу трансформаторов
Экспериментальное исследование влияния несинусоидальности напряжения на работу трансформаторов Ручное солнце. Когда термоядерные реакторы станут реальностью?
Ручное солнце. Когда термоядерные реакторы станут реальностью? Уравнения материального баланса. Уравнение Бернулли, уравнение неразрывности
Уравнения материального баланса. Уравнение Бернулли, уравнение неразрывности Кривошипно-шатунный механизм
Кривошипно-шатунный механизм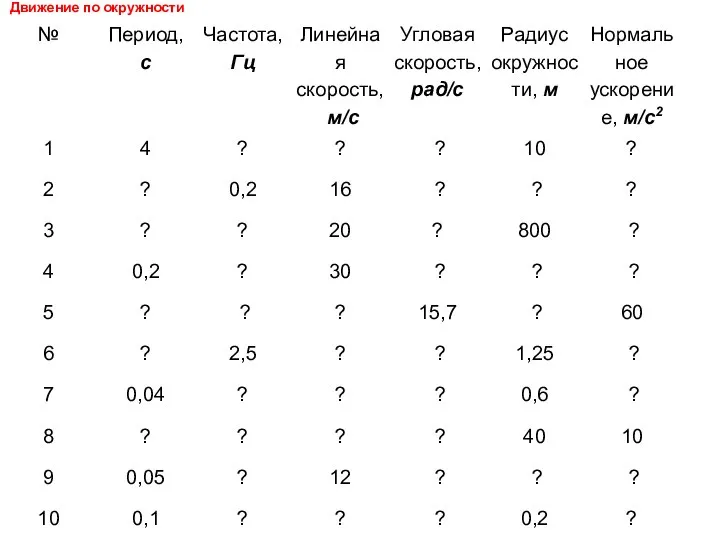 Движение по окружности
Движение по окружности Последовательное соединение проводников
Последовательное соединение проводников Vztah mezi napětím a deformací fyzikální rovnice
Vztah mezi napětím a deformací fyzikální rovnice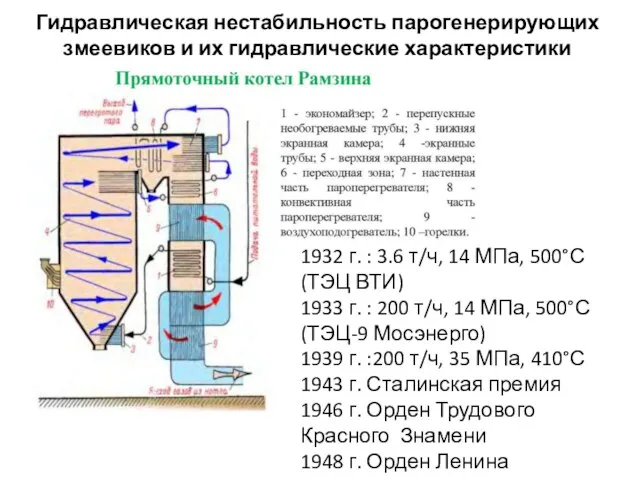 Гидравлическая нестабильность парогенерирующих змеевиков и их гидравлические характеристики
Гидравлическая нестабильность парогенерирующих змеевиков и их гидравлические характеристики Технологическая (проектно-технологическая) практика
Технологическая (проектно-технологическая) практика Физика в картинках
Физика в картинках Действие жидкости и газа на погруженное в них тело
Действие жидкости и газа на погруженное в них тело