Содержание
- 2. Методы теории решений основаны на проверке статистических гипотез о техническом состоянии объекта контроля (ОК). Правила принятия
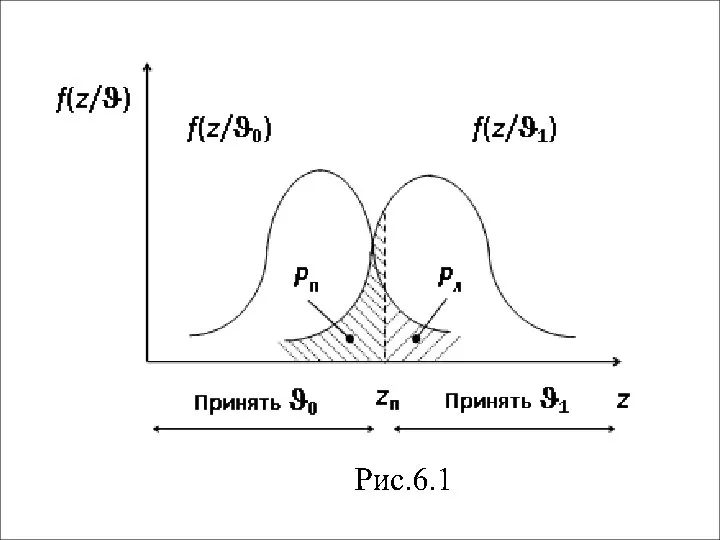
- 3. Для выбора гипотезы необходимо знать пороговое значение наблюдения , которое давало бы следующее решение: наиболее вероятна
- 4. Будем считать, что для гипотезы в пространстве наблюдений задано распределение с условной плотностью вероятности , а
- 6. Процедура принятия решения состоит в сравнении наблюдения z с некоторым пороговым значением . Причем, если ,
- 7. Аналогично для вероятности ложной тревоги получаем (6.2) Из выражений (6.1) и (6.2) следует, что, например, вероятность
- 8. Критерий Неймана-Пирсона определяет правило принятия решения из условия минимизации вероятности пропуска отказа (ошибки контроля второго рода)
- 9. В реальных случаях, когда имеется несколько наблюдений, оказывается возможным, используя метод множителей Лагранжа, наложить ограничение на
- 10. При оптимальном выборе порогового значения (допуска) для наблюдений производная функционала (6.3) по z в точке равна
- 12. Скачать презентацию








 Условие и расчет
Условие и расчет Фотоэффект. Применение фотоэффекта
Фотоэффект. Применение фотоэффекта Электрический ток
Электрический ток Электризация тел
Электризация тел Мобильный телефон с точки зрения физики
Мобильный телефон с точки зрения физики Презентация на тему Постоянные магниты Магнитное поле Земли
Презентация на тему Постоянные магниты Магнитное поле Земли  Масса. Единица массы
Масса. Единица массы Теоретические основы механики грунтов. Глава 1
Теоретические основы механики грунтов. Глава 1 Энтропия. Теорема Нернста
Энтропия. Теорема Нернста Параметрические цепи
Параметрические цепи Сила тока
Сила тока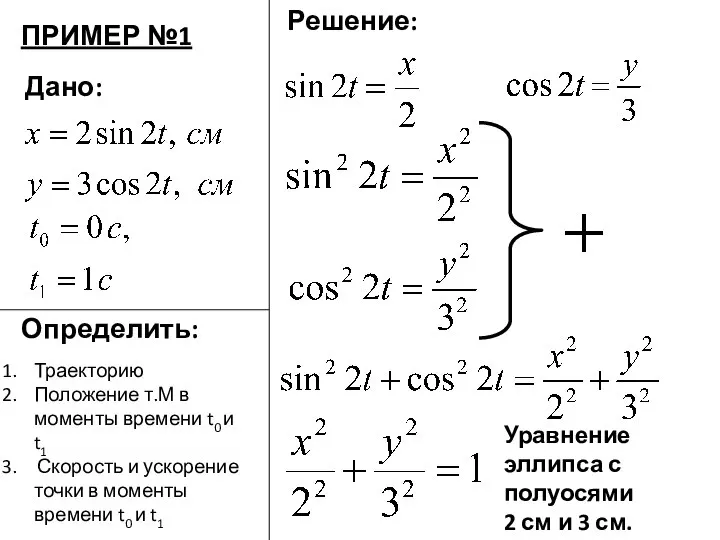 Zadacha_Kinematika_tochki_LR_2
Zadacha_Kinematika_tochki_LR_2 Физика и технология наноструктур
Физика и технология наноструктур Электромагнитная природа света. Электромагнитные явления
Электромагнитная природа света. Электромагнитные явления Электрический ток
Электрический ток Определение реакций связей твердого тела
Определение реакций связей твердого тела Основные и дополнительные средства защиты в сетях напряжением выше 1000 в
Основные и дополнительные средства защиты в сетях напряжением выше 1000 в Достижения Хладни
Достижения Хладни Итоговая контрольная работа. (7 класс)
Итоговая контрольная работа. (7 класс) Изменение внутренней энергии газа в процессе теплообмена и совершения работы. Первое начало термодинамики. Лекция 5
Изменение внутренней энергии газа в процессе теплообмена и совершения работы. Первое начало термодинамики. Лекция 5 Инструменты, механизмы и технические устройства
Инструменты, механизмы и технические устройства Законы сохранения в механике. Часть 3. Подготовка к ЕГЭ
Законы сохранения в механике. Часть 3. Подготовка к ЕГЭ Исследование магнитоупругих колебаний в магнитной пленке при сверхбыстром лазерном возбуждении с использованием техники
Исследование магнитоупругих колебаний в магнитной пленке при сверхбыстром лазерном возбуждении с использованием техники Русские изобретения, которыми пользуется весь мир
Русские изобретения, которыми пользуется весь мир Elektroemkost_1425693791_41054
Elektroemkost_1425693791_41054 Герман Гюнтер Грассман
Герман Гюнтер Грассман Уравнение плоской гармонической волны
Уравнение плоской гармонической волны Тепловые двигатели и их влияние на окружающую среду
Тепловые двигатели и их влияние на окружающую среду