Шредингер теңдеуін бөлшектердің стационар күйлеріне қатысты қарапайым есептеріне қолдану

1-мысал. «Потенциялық шұңқырдағы» бөлшек

1) п/шұңқырдағы клас. бөлшек
1) Әуелі осындай шұңқырдағы клас. бөлшекті қарастырайық.

Енді , кв. мех. заңдарына бағынатын бөлшекті қарас-йық: оның әрекеті басқаша б-ды. Мұны көрсету үшін Шр. стац. теңдеуін (15) бір өлшемді жағдай үшін жазып, шешу керек.
Бөлшек п/ш-дан өте алмайды, яғни 1 ж/е 3-аймақтарда бола алмағандықтан, осы аймақтарда бөлшекті табу ық-дығы, демек, оның т/ ф-ясы Ψ= 0.
Ψ- ф-ның үздіксіз болу шартынан ол п/ш-дың шекарасында нөлге тең болу керек, яғни мынадай шекаралық шарт орындалады:
(3)-т-дің жалпы шешуін мына түрде жазуға б-ды:
2) кв. мех. заңдарына бағынатын бөлшек

Шр-дің стац. тең-нің шешімін алу: Ψ-ф-ны анықтау

(8) - Шр-дің стац. тең-інің (15) шешімі (меншікті ф-циялары).

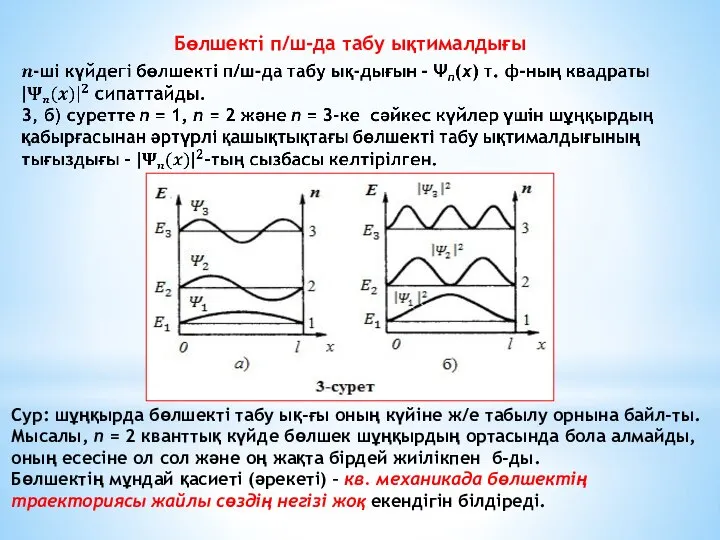
3, а) суретте n = 1, n = 2 және n = 3 күйлері үшін (9) өрнектегі энергия деңгейлеріне сәйкес келетін меншікті Ψ-функцияның сызбасы келтірілген:
Стац. күйлердегі Е эн-ның меншікті мәндері
Ψ-ф-ция шекті, үздіксіз және жатық болу к/к)
Шр. теңд-ң (15) шешімдері-
меншікті функциялар :

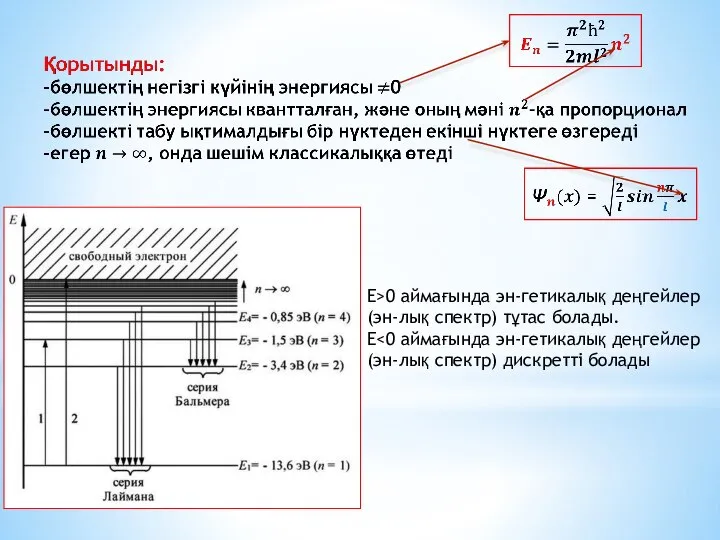
Эн. деңгей-рдің салыст-малы ар-ғын есептеу

Сур: шұңқырда бөлшекті табу ық-ғы оның күйіне ж/е табылу орнына байл-ты.
Мысалы, n = 2 кванттық күйде бөлшек шұңқырдың ортасында бола алмайды, оның есесіне ол сол және оң жақта бірдей жиілікпен б-ды.
Бөлшектің мұндай қасиеті (әрекеті) – кв. механикада бөлшектің траекториясы жайлы сөздің негізі жоқ екендігін білдіреді.
Бөлшекті п/ш-да табу ықтималдығы

E>0 аймағында эн-гетикалық деңгейлер (эн-лық спектр) тұтас болады.
E<0 аймағында эн-гетикалық деңгейлер (эн-лық спектр) дискретті болады

2-мысал. Бөлшектің потенциялық тосқауылдан өтуі

(Себебі, осы шешімдердің әрқайсысын жоғарыдағы өз теңдеулеріне қойсақ, сәйкес теңдеу орындалады, яғни нөлге тең болады: тексер!).

Бұл теңдеулерді шешіп, D және R коэффициенттерін аламыз:
(15)

Пот. тосқ-дан өткенде, бөлшек, осы тосқауылдағы «туннель» ар-лы өткендей
б-ды (штрихталған аймақ). ⇒ біз қарастырған мысал «туннельді эффект» д/а.
Клас. тұрғыда т/эф – ақылға сыймайтын, заңға қайшы келетін құбылыс болып
көрінеді. Яғни, туннельде болған бөлшек теріс кин. эн-ға ие болушы еді (E
Алайда, туннель түсінігі – ерекше, өзіндік кв-тық құб-с, кл. физ-да баламасы жоқ.
Кв. мех-да толық эн-ны - кин. және пот. деп бөлудің мағынасы жоқ, себебі
Гейз-тің анық. принц-не қайшы келеді.
Шынында да, егер бөлшектің нақты бір Т кин. эн-сы бар десек, оның нақты Р
имп-сі б-ды.
Осы сияқты, бөлш-тің нақты бір U пот. эн-сы бар деген сөз,⇒ бөлшек кеңістіктің
белгілі бір нүк-де б-ды.
Алайда, анық. принц. б-ша, бөлш-тің имп-сі мен коорд-сы бір мезетте нақты
мәнге ие бола алмайды, яғни бір мезетте Т ж/е U дәл анық-ла алмайды.