Электрическая система. Процесс

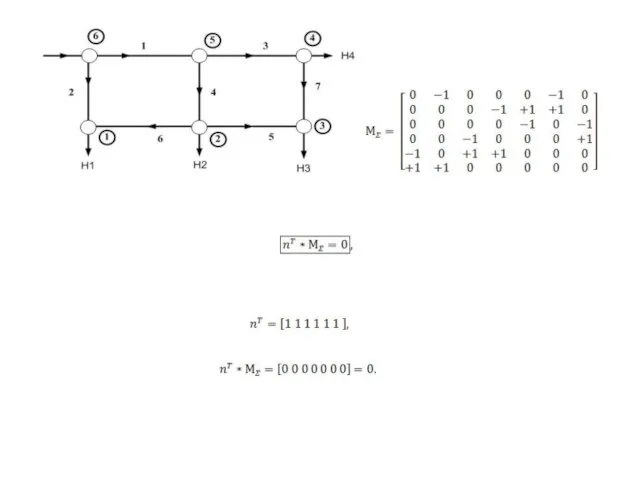
Проверка правильности получения первой матрицы соединений
где n – вектор-столбец, состоящий из единиц, характеризующий количество узлов в схеме. n=6.

Матрица ветвей дерева:
- получается исключением из первой матрицы соединений хорд.
Матрица ветвей хорд:
- получается исключением из первой матрицы соединений ветвей дерева.
Матрица М:
- составляется из матрицы
путем вычеркивания строки, соответствующей базисному узлу.

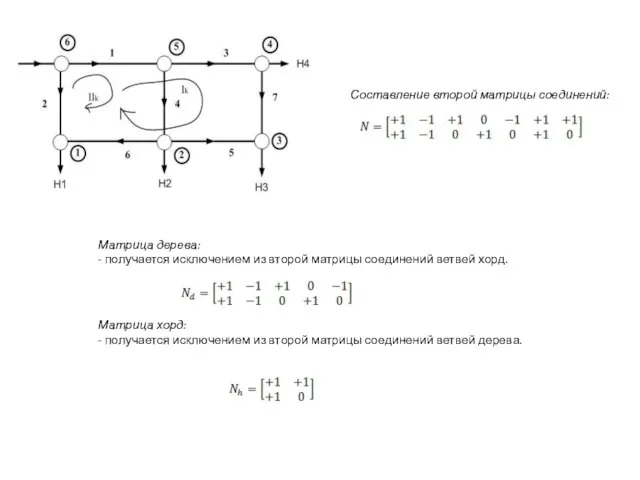
Составление второй матрицы соединений:
Матрица дерева:
- получается исключением из второй матрицы соединений ветвей хорд.
Матрица хорд:
- получается исключением из второй матрицы соединений ветвей дерева.

Расчет установившегося режима системы методом контурных токов
Из первой матрицы соединений исключается базисный узел
Из матрицы М выделяется матрица дерево
Из матрицы М выделяется матрица хорд

Матрица коэффициентов распределения для разомкнутой системы
- может быть получена непосредственно из направленного графа схемы. Столбцы матрицы Cd отвечают узлам, а строки ветвям.
Элементы матрицы коэффициентов получаются следующим образом: двигаясь от первого узла к базисному, смотрят, какие ветви встречаются на пути движения.
Сij = +1, если ветвь на пути движения совпадает с направлением движения к базисному узлу,
Сij = -1, если направление ветви на пути движения к базисному узлу противоположны,
Сij = 0, если ветвь не встречается на рассмотренном пути.
Проверка правильности получения матрицы
коэффициентов распределения
где E здесь – единичная матрица.
Проверяем матрицу Сd

Матрица контурных сопротивлений
Обращаю внимание на размерность
[2*7]х[7*7]х[7*2] = [2*2]
Матрица контурных проводимостей
Определение контурного тока

Определение токов в ветвях, возникающих под действием ЭДС
Токи в ветвях дерева, определяемые задающими токами в узлах
Токи в ветвях
Матрица узловых напряжений
Напряжение в узлах
где n – матрица, характеризующая количество узлов в схеме;
базисное напряжение,

Расчет установившегося режима замкнутой системы на основе обобщенного уравнения состояния
Проверка
. Составление обобщенного уравнения состояния электрической цепи
где матрица А – квадратная матрица, число столбцов которой равно числу ветвей, а число строк – сумме независимых узлов и независимых контуров; матрица F – объединенная матрица, включающая в себя вектор задающих токов и вектор ЭДС контуров.
Матрица А:

Матрица F:
Токи в ветвях:

Проверка правильности расчета по первому закону Кирхгофа
(по току в узлах):
где допустимая погрешность (ошибка), которая приравнивается к 5%.
3. Определение узловых напряжений
где Id – токи ветвей дерева.
Токи ветвей дерева:
Узловые напряжения:

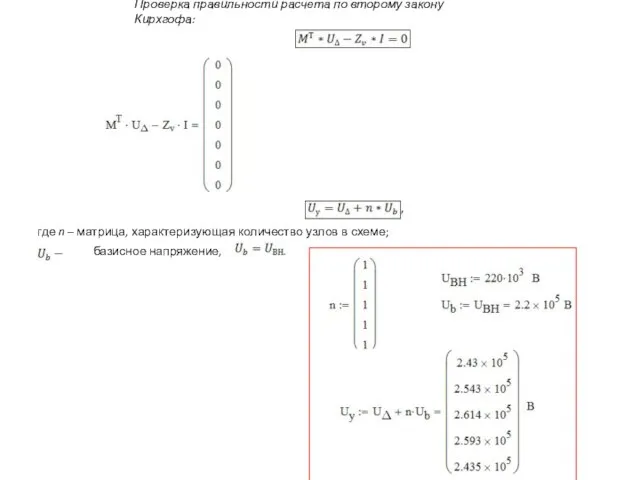
Проверка правильности расчета по второму закону Кирхгофа:
4. Определение напряжений в узлах
где n – матрица, характеризующая количество узлов в схеме;
базисное напряжение,

Расчет установившегося режима системы
методом узловых напряжений
В качестве неизвестных переменных принимают узловые напряжения.
1. Определение узловых напряжений
где Yу – матрица узловых проводимостей. Составляется непосредственно по графу сети.
Матрица узловых проводимостей:
Порядок матрицы узловых проводимостей равен числу независимых узлов схемы. Элементы матрицы Yу получается по правилу:
- элементы на главной диагонали Yii – сумма проводимостей ветвей, примыкающих к узлу i,
- элементы Yij= Yji – это проводимость ветви между узлами i и j с обратным знаком.
Матрица узловых проводимостей всегда симметрична.

Узловые напряжения:
2. Определение напряжений в узлах
где n – матрица, характеризующая количество узлов в схеме;
базисное напряжение,