Презентация на тему Колебания

Колебания
Периодическая величина: функция f(t) есть периодическая функция (величина) с периодом Т если
f(t)=f(t+T)
Колебаниями называются процессы, при которых какая-либо величина (физическая, географическая или любая другая) многократно принимает через равные последовательные промежутки времени одни и те же значения (или приблизительно одни и те же).

Свободные и вынужденные колебания
Если система каким-либо образом выведена из равновесия и затем предоставлена самой себе (источник устранен), то в ней происходят колебания, которые называются свободными или собственными. Например, маятник Фуко или боксерская груша, выведенная из положения равновесия однократным ударом или удар лектора по крышке стола.
Если же система колеблется под воздействием периодически изменяющейся внешней силы, то такие колебания называются вынужденными. Например, мост под воздействием периодически повторяющейся внешней силы (прохода строевым шагом колонны солдат).

Частота, фаза и амплитуда
Частота v — число колебаний в единицу времени, T — период колебаний, то есть время, через которое значения колеблющейся величины начинают повторяться.
Если период колебания равен 1 с то частота равна 1Гц
Фазой колебаний называется величина
ϕ0— начальная фаза колебаний, то есть фаза при t = 0. Фаза характеризует отклонение величины х от нулевого значения в данный момент времени и определяется с точность до произвольного слагаемого кратного 2π
Амплитуда – максимальное отклонение от положения равновесия

Гармонические колебания
Во многих случаях разнообразные периодические процессы могут быть представлены как суперпозиция гармонических колебаний. Гармоническими называются колебания с постоянной амплитудой А, происходящие по закону синуса или косинуса, то есть когда изменение физической величины x(t) выражается формулой:
— круговая или циклическая частота колебаний.
Пример: проекция на ось х точки двигающейся равномерно по окружности радиуса R: х=Rsinα=Rsinωt

Дифференциальным уравнением гармонических колебаний
Скорость и ускорение в гармоническом колебательном движении точки определяются соответствующими производными по времени:
- Скорость изменяется по гармоническому закону, но ее амплитуда больше амплитуды х в ω раз и опережает х на π/2
- Ускорение изменяется по гармоническому закону, но его амплитуда больше в ω2 раз и опережает х на π (т.е. в противофазе с х)
Это дифференциальное уравнение гармонических колебаний. Уравнением такого типа описываются любые гармонические колебания.

Гармонический осциллятор
Тело массы m, колеблющееся горизонтально под действием силы упругости пружины F=-kx (k — коэффициент упругости, x — смещение тела относительно положения равновесия, знак “минус” означает, что упругая сила направлена противоположно направлению смещения x) согласно 2-му закону Ньютона запишем:
где
имеем
Частота ω0 называется собственной частотой данного гармонического осциллятора. Если вертикально, то появляется лишь начальное смещение х0: кх0=mg которое потом сокращается.
Решением является уравнение для гармонического осциллятора

Кинетическая и потенциальная энергии
Если проходим через положение равновесия, то вся энергия переходит в кинетическую (потенциальная =0) и наоборот в крайнем положении.
Верно так как средние значения sin2 и cos2 равны по ½ каждое
Совершив преобразования над sin2 и cos2 можно показать, что T и U изменяются с частотой 2ω0 . Т.е. энергия от T к U и наоборот в процессе колебаний перекачивается в два раза быстрее.

Квазиупругие силы
Силы любого происхождения, пропорциональные величине отклонения системы от положения равновесия и направленные к положению равновесия называются квазиупругими силами. Колебания под действием квазиупругих сил будут гармоническими.
Т.е принципиальное отличие квазиупругих (-кх) от постоянных (независящих от расстояния и направления перемещения) сил в том, что воздействие постоянной силы приводит лишь к смещению положения равновесия ничего не меняя в характере самого движения.

Физический маятник
Физическим маятником называется твердое тело, которое может вращаться вокруг горизонтальной оси (возможно только при условии, что центр масс тела не лежит на этой оси). Т.е. нужен ненулевой момент сил. Движение такого маятника можно описать основным уравнением динамики для вращательного движения тела:
где I – момент инерции маятника относительно горизонтальной оси вращения через точку О. Внешних сил здесь две: сила F упругого происхождения (изгибает ось), действующая на маятник со стороны оси в точке 0 и сила тяжести P , приложенная в центре масс. Величина и направление силы F нам неизвестны, но это неважно, так как она проходит через ось вращения и поэтому ее момент равен нулю (плечо равно нулю).

Физический маятник
Момент силы тяжести:
= - Rmgsinα =–Pв
где в = Rsinα - плечо силы тяжести. Знак «минус» означает, что при α >0, то есть при отклонении против часовой стрелки момент силы вызывает вращение по часовой стрелке (в направлении противоположном первоначальному отклонению). Т.е момент силы тяжести действует аналогично квазиупругой силе –kx . Итак, получаем:
I α″ = –mgRsinα
При малых α (при α <<1 в радианной мере) sinα ≈ α и
α″ + ω2α = 0 , где ω2 =

Физический маятник
В результате имеем дифференциальное уравнение гармонических колебаний, решением которого как нам уже известно является функция:
α (t) = Asin(ωt+φ)
где циклическая частота
а период колебаний

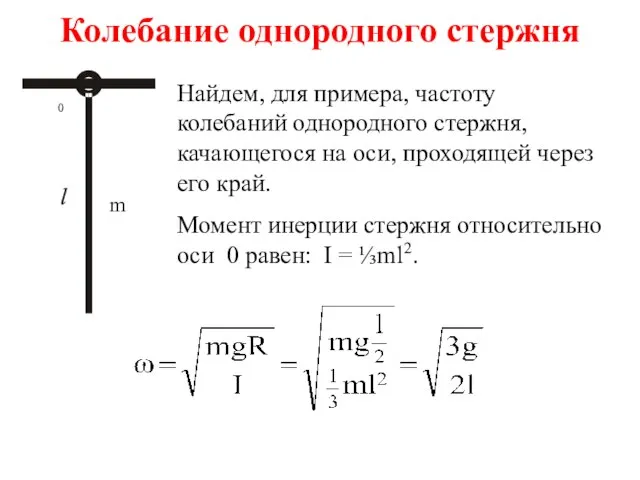
Колебание однородного стержня
Найдем, для примера, частоту колебаний однородного стержня, качающегося на оси, проходящей через его край.
Момент инерции стержня относительно оси 0 равен: I = ⅓ml2.

Математический маятник
Математическим маятником называется материальная точка, подвешенная на нерастяжимой нити. Он оказывается частным случаем физического маятника.
Момент инерции материальной точки
I = ml2
Измерив период колебаний маятника, можно определить ускорение свободного падения g в данном месте. Т.е. из за разного характера распределения массы есть отличие в частоте колебаний стержня и математического маятника.

Затухающие колебания
Если нельзя пренебрегать сопротивлением среды при записи 2-го закона Ньютона для движения тела под действием упругой силы, то его надо дополнить некоторой функцией, отражающей свойства сил сопротивления (сил трения).
Например, если тело все время движется в жидкости с малыми скоростями, то сила трения пропорциональна скорости и второй закон Ньютона записывается так:
или в стандартном для дифференциальных уравнений виде :

Затухающие колебания
Обозначим: (как и ранее) и
дифференциальное уравнение затухающих колебаний:
Решение уравнений такого типа в математике хорошо известно и в нашем случае выглядит так:
Заметим, что здесь фигурирует не собственная частота колебаний ω0 , а частота ω , которая зависит от коэффициента затухания β:

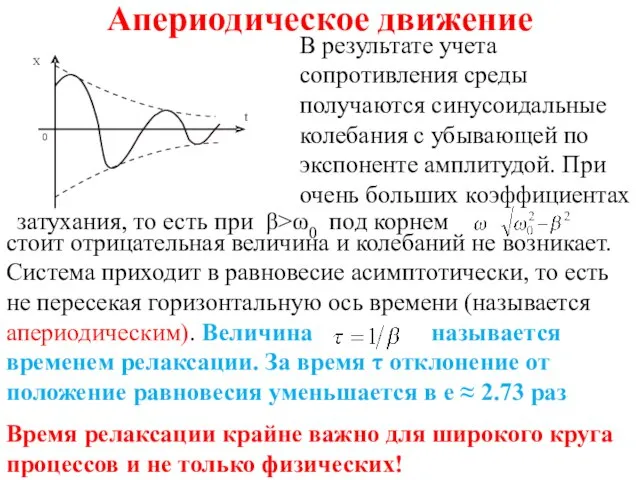
Апериодическое движение
В результате учета сопротивления среды получаются синусоидальные колебания с убывающей по экспоненте амплитудой. При очень больших коэффициентах
стоит отрицательная величина и колебаний не возникает. Система приходит в равновесие асимптотически, то есть не пересекая горизонтальную ось времени (называется апериодическим). Величина называется временем релаксации. За время τ отклонение от положение равновесия уменьшается в e ≈ 2.73 раз
Время релаксации крайне важно для широкого круга процессов и не только физических!
затухания, то есть при β>ω0 под корнем

Декремент затухания
Быстроту затухания описывают также с помощью декремента затухания или с помощью логарифмического декремента затухания. Декрементом затухания Δ называют отношение двух последовательных амплитуд:
Логарифмическим декрементом затухания δ называют натуральный логарифм обычного декремента затухания:
δ = lnΔ = βT
если величина β фиксирована, то величина δ прямо пропорциональна периоду колебаний. Например, если δ=0.01 то амплитуда уменьшится в e раз после 100 колебаний. Быстроту затухания колебаний определяется β= δ/T.
Добротность системы Q. При больших добротностях δ≈π/Q

Вынужденные колебания
Колебания, происходящие в системе под действием периодически изменяющейся силы, называются вынужденными.
Пусть тело колеблется под действием упругой силы и на него действует внешняя сила :
Fвнеш (t)= F0sinΩt
учитывая используемые выше уравнения, второй закон Ньютона запишем в виде:
Подобные уравнения описывают широкий спектр процессов вплоть до описания движения доменных стенок в магнитных материалах, где m эффективная масса доменной стенки.

Вынужденные колебания
Опыт показывает, что если вынуждающая сила действует достаточно долго, то груз колеблется с частотой вынуждающей силы Ω и с постоянной амплитудой. Поэтому можно предположить, что раз вынуждающая сила гармоническая, то и установившиеся колебания также будут гармоническими:
x = Asin(Ωt + φ)
Надо найти амплитуду А и начальную фазу φ этого колебания. Для этого можно взять первую и вторую производную x подставить все в уравнение движения. Если произвести ряд громоздких преобразований, то можно получить следующие соотношения:

Амплитуда и фаза
Разность фаз колебаний вынуждающей силы и груза φ :
Прямой подстановкой можно убедиться, что это решение удовлетворяет исходному уравнению движения.
В полученном решении и амплитуда, и фаза зависят от частоты вынуждающей силы.

Резонанс
Есть зависимость амплитуды от частоты и значит при некоторой частоте возможна максимальная амплитуда. Это будет тогда, когда знаменатель в выражении движения достигнет минимума. Чтобы найти минимум, приравняем нулю производную по частоте Ω знаменателя:
Это кубическое уравнение имеет, естественно, три корня:
Ω1 = 0 и
Это есть точки экстремума знаменателя. Решение Ω1 = 0 соответствует максимуму знаменателя. При этом амплитуда

Резонансная частота
Из двух оставшихся решений отрицательное отбрасываем как не имеющее физического смысла, так как частота отрицательной быть не может. Следовательно, амплитуда будет максимальной при следующей частоте вынуждающей силы:
Эта частота называется резонансной, а само явление возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающей силы к некоторой частоте называется резонансом.
Отметим, что резонансная частота не совпадает с собственной частотой колебаний системы ω0, но близка к ней и тем ближе, чем меньше трение в системе.

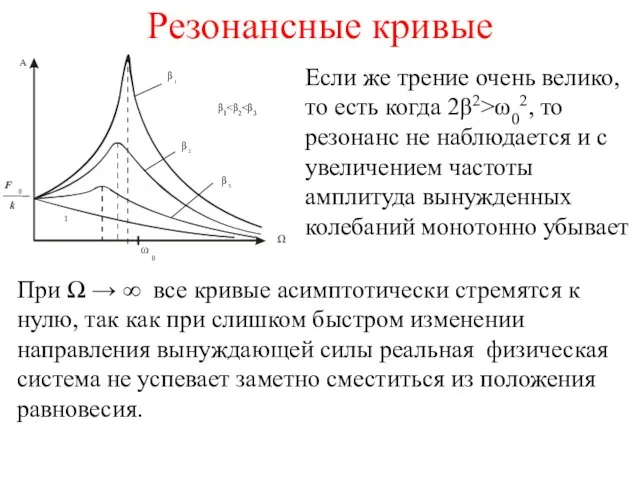
Резонансные кривые
Если же трение очень велико, то есть когда 2β2>ω02, то резонанс не наблюдается и с увеличением частоты амплитуда вынужденных колебаний монотонно убывает
При Ω → ∞ все кривые асимптотически стремятся к нулю, так как при слишком быстром изменении направления вынуждающей силы реальная физическая система не успевает заметно сместиться из положения равновесия.

Резонанс в повседневной жизни
Явление резонанса может наблюдаться в любых физических (и не только) явлениях. Может быть как вредным, так и полезным. Например, при конструировании самолета жизненно важно, чтобы собственная частота вибраций всех его частей (фюзеляж, крылья и т.п.) существенно отличалась от частот колебаний, которые могут быть возбуждены при полете, например, пропеллером и турбиной (которая крутится на определенной частоте).
В радиотехнике же резонанс часто оказывается полезным: всем хорошо известно, что прием радио и телепередач основан именно на резонансе.
Землетрясение ! Резонансную частоту домов делать подальше от частоты толчков земной коры
В 5-й главе ветхого завета , где говорится о разрушении храма (резонанс звука и собственных колебаний стены???) «…а на 7 день как закричит …он и рухнул». Если в конструкциях использовались элементы с собственной частотой в звуковом диапазоне!

20 мая 2010 на мосту через Волгу в Волгограде были зафиксированы вынужденные резонансные колебания амплитудой до 1 м. Техническое состояние 7-километрового моста через Волгу не пострадало.

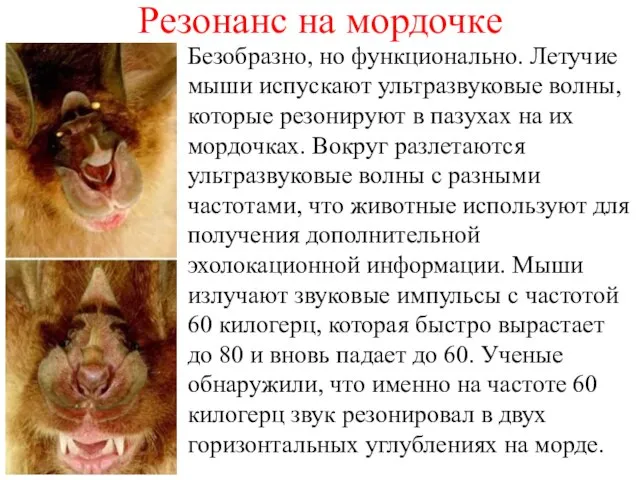
Резонанс на мордочке
Безобразно, но функционально. Летучие мыши испускают ультразвуковые волны, которые резонируют в пазухах на их мордочках. Вокруг разлетаются ультразвуковые волны с разными частотами, что животные используют для получения дополнительной эхолокационной информации. Мыши излучают звуковые импульсы с частотой 60 килогерц, которая быстро вырастает до 80 и вновь падает до 60. Ученые обнаружили, что именно на частоте 60 килогерц звук резонировал в двух горизонтальных углублениях на морде.

Загадка веревочных колец
На рисунке показаны кольца у веревок, сброшенных с разной высоты при разных скоростях: (a) высота: 1.2 см, скорость: 26 см в секунду; (b) высота: 30 см, скорость: 2.3 см в секунду; (c) высота: 80 см, скорость: 100 см в секунду.
Эластичные веревки да и макароны относят к особому классу материалов из разряда нелинейных динамических систем, и в их поведении разобраться непросто.