Механика многофазных сред

МЕТОДЫ ИЗУЧЕНИЯ ФИЗИЧЕСКИХ ЯВЛЕНИЙ
Феноменологическим метод игнорирует микроскопическую структуру вещества и рассматривающий его как сплошную среду (континуум).
Среда, которую допустимо рассматривать как непрерывную (континуум), пренебрегая дискретным ее строением называется сплошной средой (СС).
Различают СС:
однородная, неоднородная, изотропная, анизотропная, однофазная, многофазная.
Статистический метод (СМ) – метод изучения физических явлений на основе исследования внутренней структуры вещества и обобщения их в макросвязи. Задача СМ – получение макроскопических характеристик по микроскопическим свойствам среды.

Однородная СС – это СС, в разных точках которой ее физические свойства одинаковы при одинаковых температуре и давлении.
Неоднородная СС – это СС, в разных точках которой ее физические свойства различны при одинаковых температуре и давлении.
Изотропная СС - это СС, физические свойства которой не зависят от направления.
Анизотропная СС - СС, физические свойства которой различны по разным направления.
Однофазная СС – СС одно- или многокомпонентная среда, физические свойства которой в пространстве могут изменяться только непрерывно.
Многофазная СС - СС одно- или многокомпонентная, состоящая из ряда однофазных частей, на границах которой ее физические свойства меняются скачком.
Феноменологический метод (ФМ) дает возможность установить общие соотношения между параметрами, характеризующими рассматриваемое явление в целом. Роль физической среды учитывается через коэффициенты (теплофизические свойства), полученные из опыта.

Достоинство ФМ
в установлении общих связей между параметрами процесса с использованием эмпирической информации о процессе. Причем точность метода предопределена точностью данных из опыта. Недостаток ФМ – в наличии эмпирической информации.
Достоинство СМ
в получении искомых соотношений (законов) по заданным свойствам микроскопической структуры среды без дополнительного эксперимента. Здесь среда рассматривается как некоторая система, состоящая из огромного числа молекул, ионов, атомов с заданными свойствами. Недостаток СМ – сложность обобщения этих зависимостей и проблемы реализации метода, т.к. необходимо знать ряд параметров, которые могут быть определены в специальных разделах физики, химии, биологии и других областях знаний.

ОСНОВНЫЕ ГИПОТЕЗЫ МЕХАНИКИ СПЛОШНОЙ СРЕДЫ
Справедливость классической механики Ньютона
скорости малы по сравнению со скоростью света
рассматриваются объекты большие, чем объекты микромира, изучаемые квантовой механикой
Справедливость классической термодинамики
Термодинамического равновесное состояние жидкости можно определить с помощью нескольких макроскопических параметров (плотности, давления, температуры, скорости, объем).
Справедливость схемы сплошной среды
Все тела состоят из отдельных частиц, но их число велико в любом существенном для нас объёме, поэтому тело можно приближённо рассматривать как среду, заполняющую просранство сплошным образом (материальный континуум).
Жидкая частица - малый объем сплошной среды, который при движении деформируется, при этом его масса не смешивается с окружающей средой. К жидкой частице применимы все законы механики.

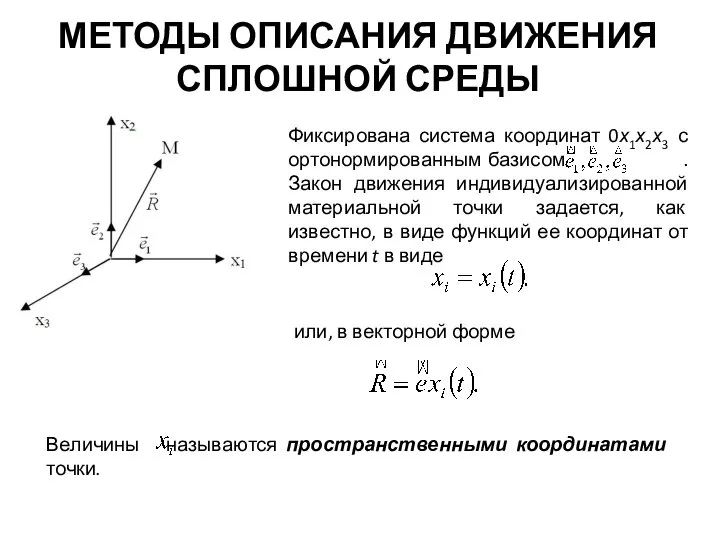
МЕТОДЫ ОПИСАНИЯ ДВИЖЕНИЯ СПЛОШНОЙ СРЕДЫ
Фиксирована система координат 0х1х2х3 с ортонормированным базисом . Закон движения индивидуализированной материальной точки задается, как известно, в виде функций ее координат от времени t в виде
или, в векторной форме
Величины называются пространственными координатами
точки.

Метод Лагранжа
Метод Эйлера
При лагранжевом подходе интересуются тем, что происходит с индивидуальными точками (частицами) сплошной среды. Чтобы отличить одну индивидуальную частицу от другой, надо на них “поставить метки”. Это можно сделать, если присвоить каждой частице свой набор из трех чисел, который играет роль “имени”. Эти числа называют лагранжевыми (материальными) координатами и часто обозначают буквами ξ1, ξ2, ξ3. Лагранжевы координаты индивидуальной точки не меняются в процессе движения.
При лагранжевом описании все величины рассматриваются как функции лагранжевых координат (ξ1, ξ2, ξ3) и времени t. В качестве ξ1, ξ2, ξ3 часто используют – значения координат точек пространства, в которых рассматриваемые индивидуальные частицы находились в начальный момент времени.

Законом движения называются функции, описывающие зависимость пространственных координат индивидуальных точек от времени t.
Закон движения записывается в виде:
Компоненты скорости и ускорения частиц сплошной среды в декартовой системе координат при лагранжевом описании вычисляются по формулам:
где для краткости использовано обозначение ξ = (ξ1, ξ2, ξ3).

При эйлеровом подходе интересуются тем, что происходит в точках пространства, через которые движется среда. Величины, характеризующие движение сплошной среды, рассматриваются при эйлеровом подходе как функции пространственных координат
и времени t. Например, величина – это скорость частицы сплошной среды, которая в момент времени t находится в точке пространства с координатами
.

ЛОКАЛЬНАЯ И СУБСТАНЦИОНАЛЬНАЯ ПРОИЗВОДНАЯ
Скорость изменения со временем любого свойства A, например скорости, плотности, температуры фиксированной материальной точки движущейся сплошной среды, называется субстанциональной (материальной, индивидуальной или полной) производной по времени и обозначается символом
.
При лагранжевом описании индивидуальная производная есть просто частная производная по времени при постоянных ξi:
.

При эйлеровом описании она называется также полной производной и вычисляется по формуле:
или, в краткой записи:
.
Здесь
– компоненты вектора скорости в системе координат .
.
характеризует скорость изменения А в фиксированной точке пространства. Эта производная называется локальной
Первое слагаемое – это частная производная по времени при постоянных пространственных координатах
Второе слагаемое конвективная производная. Она характеризует изменение A за счет перемещения материальной точки в пространстве

ЗАКОН ДВИЖЕНИЯ СПЛОШНОЙ СРЕДЫ В СИСТЕМЕ ЭЙЛЕРА И ЛАГРАНЖА
Ускорение, по определению, есть скорость изменения скорости индивидуальной частицы среды. Поэтому
вычисляется как индивидуальная производная по времени. При эйлеровом описании формула для ускорения имеет вид
Лагранжев и эйлеров подходы эквивалентны: если все интересующие величины заданы в рамках одного из них, то можно найти описание в рамках другого подхода.

и требуется найти А как функцию эйлеровых (пространственных) координат. Рассмотрим закон движения
Выразим с его помощью Лагранжевы координаты ξi через xi, t:
и подставим эти соотношения в выражение для
Получим А как функцию эйлеровых координат:
Переход от лагранжева описания к эйлерову.
Пусть некоторая величина А задана как функция лагранжевых координат

Переход от эйлерова описания к лагранжеву
Чтобы перейти от эйлерова описания к лагранжеву, нужно найти решение системы обыкновенных дифференциальных уравнений:
удовлетворяющее начальным условиям
Это решение
найденное для всевозможных значений параметров ξ1, ξ2, ξ3 и есть закон движения.
Пусть В известна как функция эйлеровых координат:
Подставляя в это выражение найденные зависимости
получим В как функцию лагранжевых переменных:

СКАЛЯРНЫЕ И ВЕКТОРНЫЕ ПОЛЯ
Если в каждой точке области пространства D и каждому моменту времени t поставлено в соответствие значение скалярной (векторной) величины, то говорят, что в области D задано скалярное (векторное) поле. Таким образом, под полем какой-либо величины понимается совокупность ее значений, заданных в каждой точке области D и в заданном интервале времени. Например, если заданы функции скалярных величин
- скалярные поля плотности и температуры
Если же дана векторная функция
- векторное поле скоростей
понятие поля физической величины применимо при описании движения только с помощью метода Эйлера

Задача №1
Задано поле скоростей
Найти закон движения материальной точки в системе Лагранжа
Задача №2
Задано поле скоростей в системе Эйлера
Найти закон движения материальной точки в системе Лагранжа
Задача №3
Известно поле скоростей в системе Эйлера
Найти скорость частицы в момент времени t, т.е.
Задача №4
Дано поле скоростей
Найти поле ускорений и ускорение частицы