Содержание
- 2. Лекция № 1. Введение в курс. Электрические цепи Введение (среда Multisim) Основные понятия теории цепей и
- 3. Список литературы: - Введение в Multisim. Трёхчасовой курс. – 2006 - Multisim 11 User Guide -
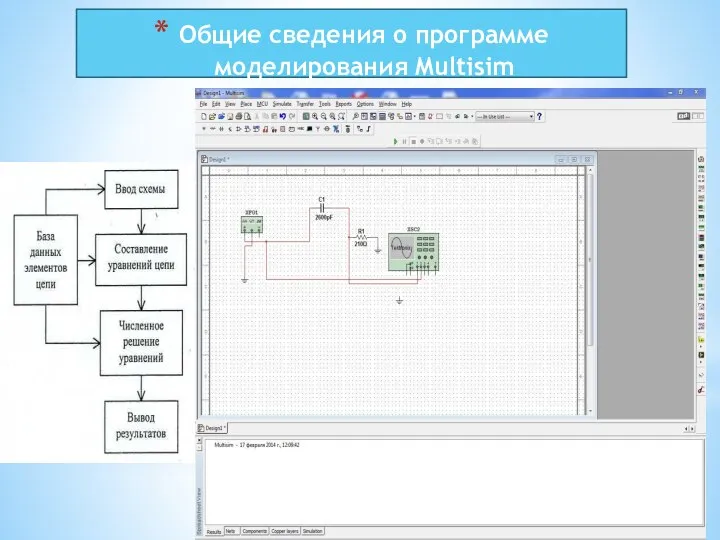
- 4. Общие сведения о программе моделирования Multisim
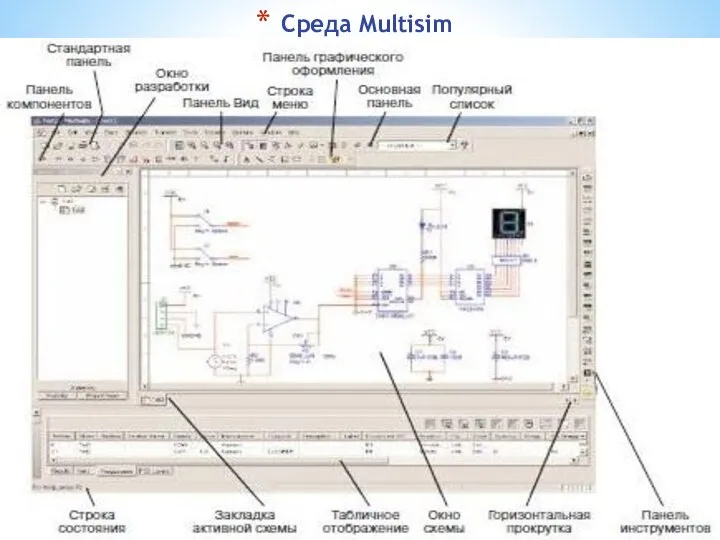
- 5. Среда Multisim
- 8. База данных Master Database разделена на группы: 1) Sources. Cодержит все источники напряжения и тока, заземления.
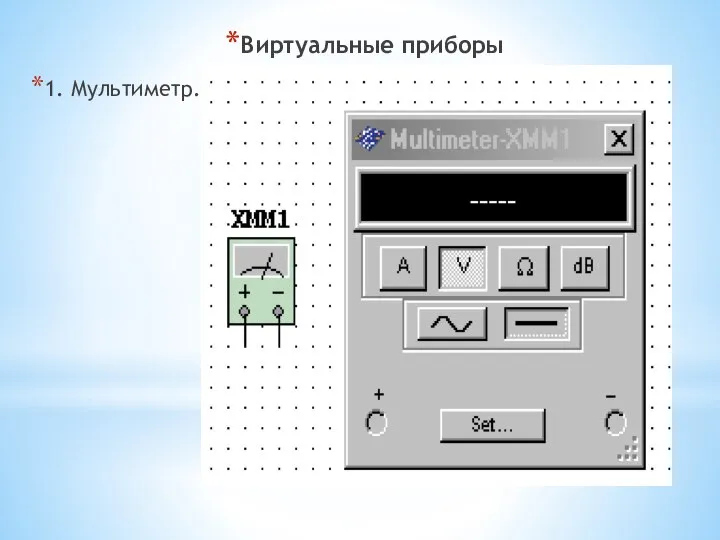
- 9. Виртуальные приборы 1. Мультиметр.
- 10. Генератор сигналов
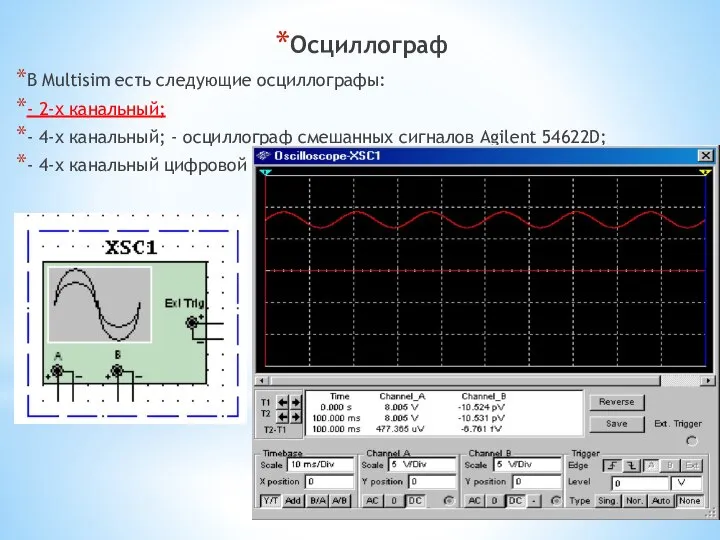
- 11. Осциллограф В Multisim есть следующие осциллографы: - 2-х канальный; - 4-х канальный; - осциллограф смешанных сигналов
- 12. Построитель частотных характеристик (Боде Плоттер) Отображает относительный фазовый или амплитудный отклик входного и выходного сигналов. Для
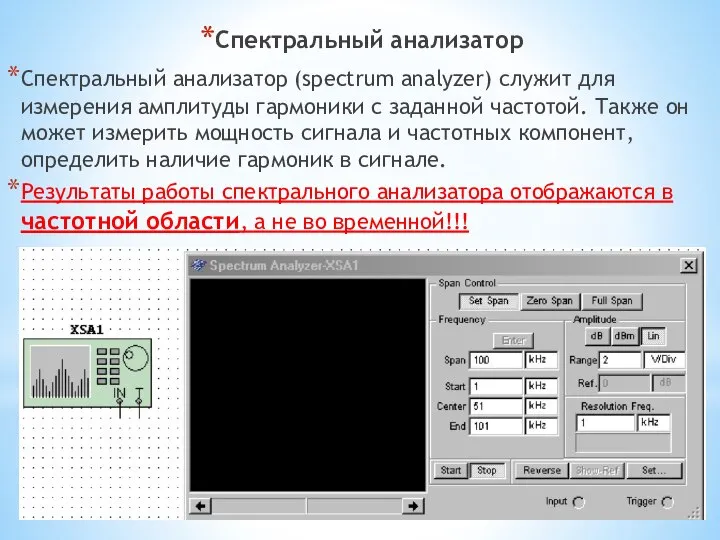
- 13. Спектральный анализатор Спектральный анализатор (spectrum analyzer) служит для измерения амплитуды гармоники с заданной частотой. Также он
- 14. Ваттметр Прибор предназначен для измерения мощности и коэффициента мощности.
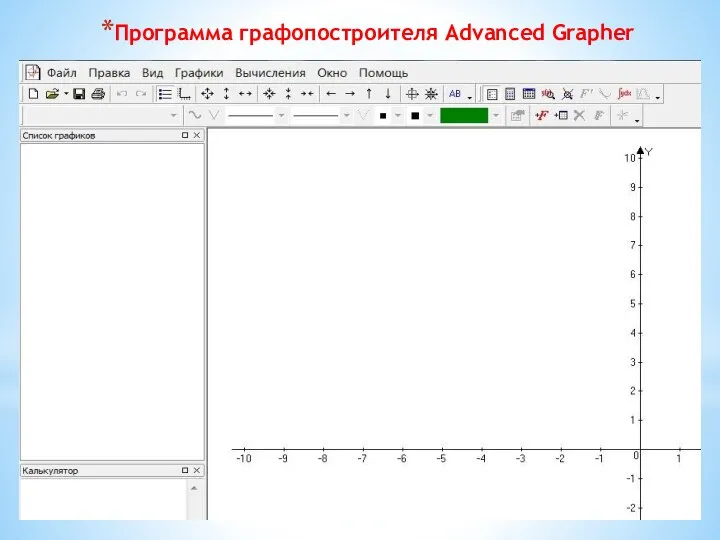
- 15. Программа графопостроителя Advanced Grapher
- 16. Программа Advanced Grapher позволяет: 1. Строить разнообразные графики на плоскости. 2. Проводить исследование функций. 3. Находить
- 17. Задание на лабораторную работу №1 1. Изучить основы работы в среде Multisim в соответствии с руководством
- 18. Этапы развития Электроники ПЕРВЫЙ ЭТАП 1887 году нем. физик Г. Герц эксперементально показал существование электромагнитных волн.
- 19. 1. Введение Определение: схемотехника, как научно-техническое направление, охватывает проблемы анализа и синтеза электронных устройств радиотехники, связи,
- 20. ПРОЕКТИРОВАНИЕ включает: - синтез — создание схемы некоего устройства из отдельных деталей или блоков. - анализ
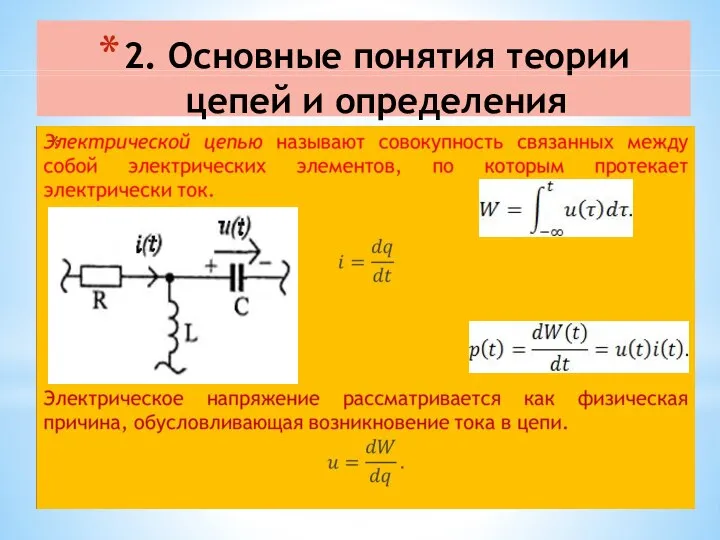
- 21. 2. Основные понятия теории цепей и определения
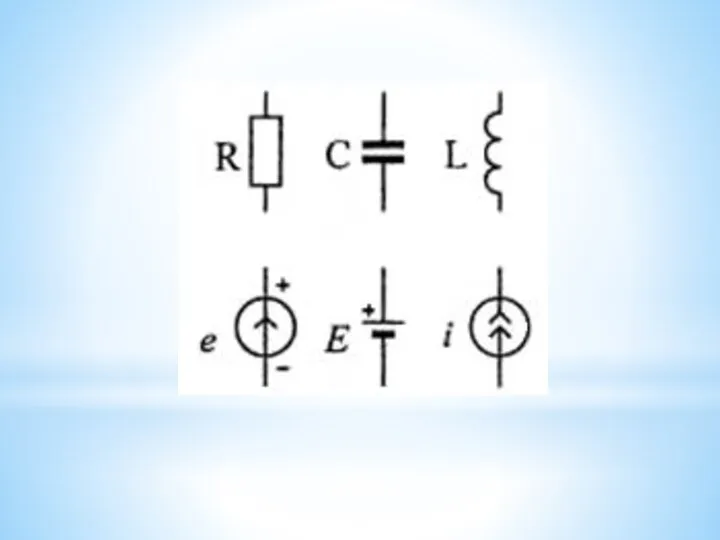
- 22. 3. Элементы электрических цепей Идеальный резистор - это элемент, в котором электрическая энергия превращается в тепло.
- 23. Уравнения идеальных элементов Уравнение резистора Уравнение конденсатора вольткулонная характеристика конденсатора Q=Си, Уравнение индуктивности полный магнитный поток
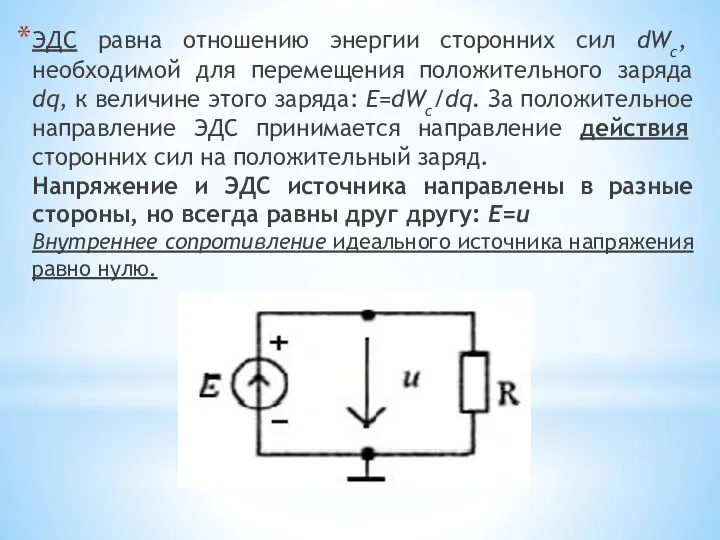
- 25. ЭДС равна отношению энергии сторонних сил dWс, необходимой для перемещения положительного заряда dq, к величине этого
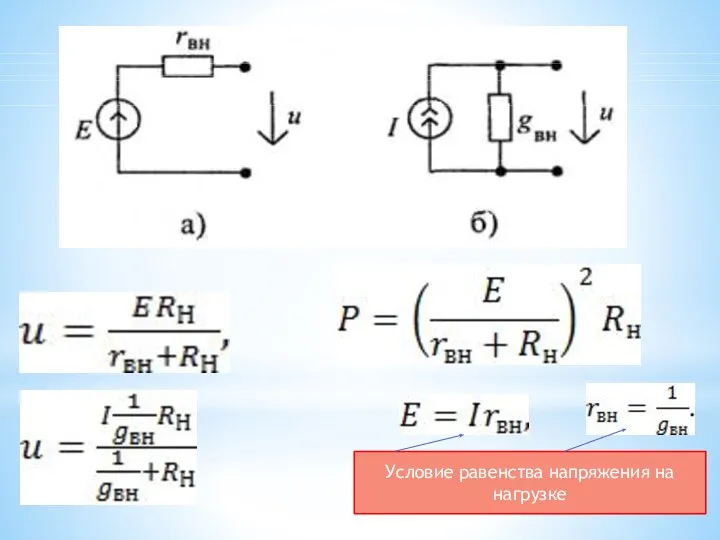
- 26. . Условие равенства напряжения на нагрузке
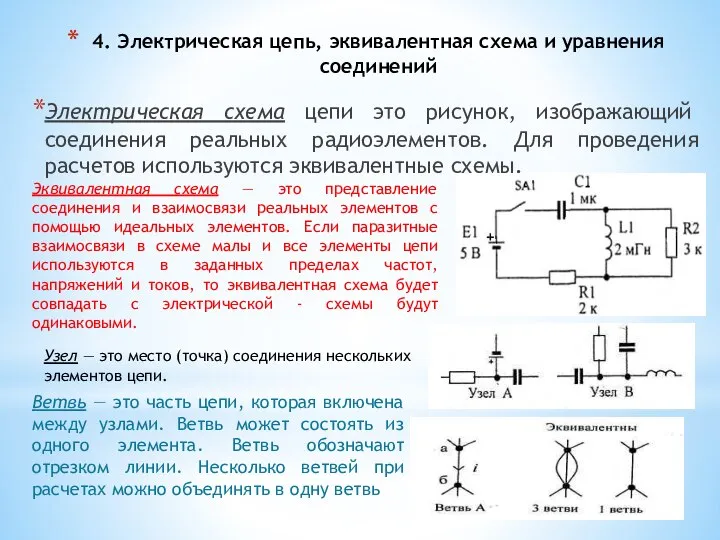
- 27. 4. Электрическая цепь, эквивалентная схема и уравнения соединений Электрическая схема цепи это рисунок, изображающий соединения реальных
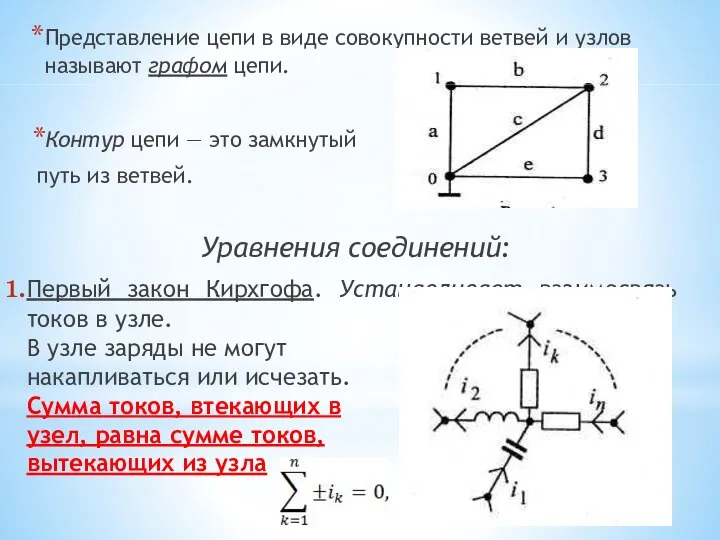
- 28. Представление цепи в виде совокупности ветвей и узлов называют графом цепи. Контур цепи — это замкнутый
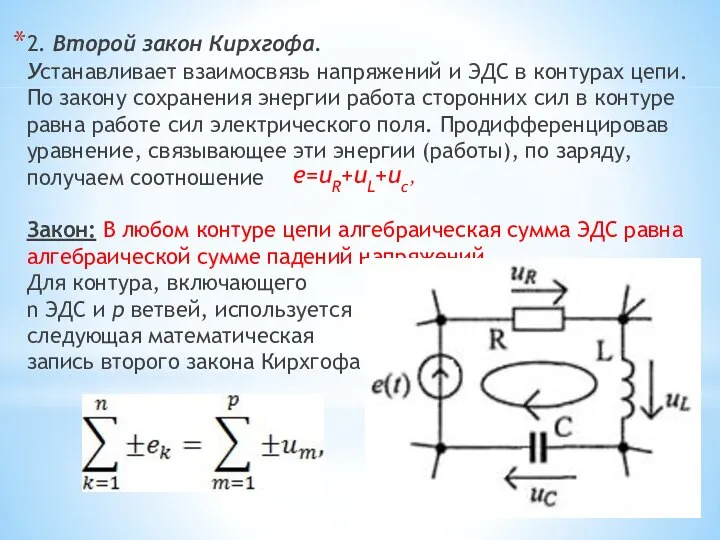
- 29. 2. Второй закон Кирхгофа. Устанавливает взаимосвязь напряжений и ЭДС в контурах цепи. По закону сохранения энергии
- 30. Пример. Дана цепь. Решение. По второму закону Кирхгофа: e(t)=uR+uL+uc, или Дифференцируя это выражений получим дифференциальное уравнение
- 31. Потенциальная диаграмма Под потенциальной диаграммой понимают график распределения потенциала вдоль какого-либо участка цепи, или замкнутого контура.
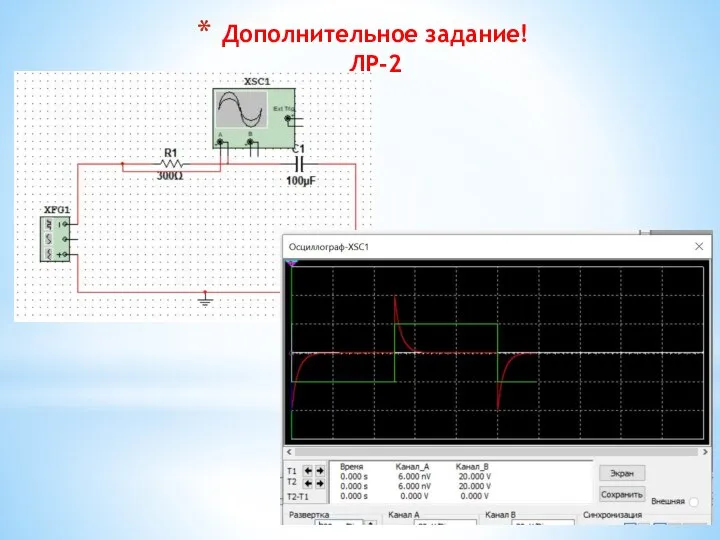
- 32. Дополнительное задание! ЛР-2
- 33. Лекция № 2. Электрические цепи при гармоническом воздействии 1. Гармонические колебания 2. Уравнения элементов цепи в
- 34. 1. Гармонические колебания Единственные сигналы, форма которых при прохождении через линейные цепи не будет искажаться, —
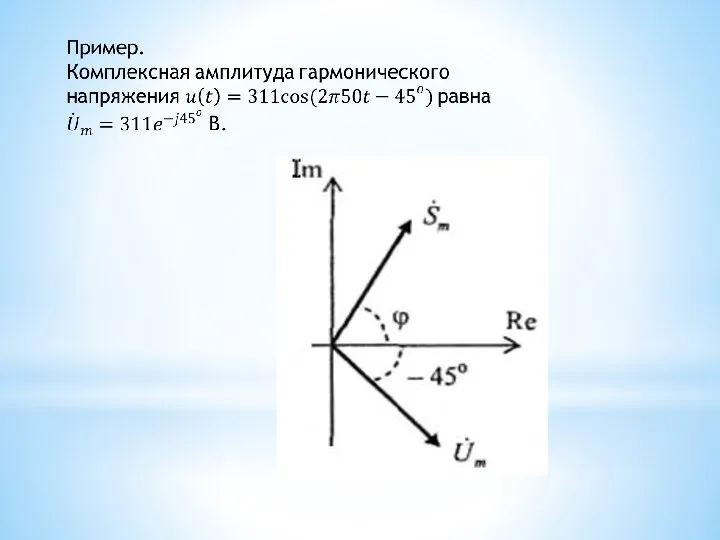
- 35. Комплексное представление гармонического сигнала. Используя формулу Эйлера: ejx=cosx+jsinx, где получим, где Re — обозначение взятия вещественной
- 37. 2. Уравнения элементов цепи в комплексной форме
- 40. 3. Комплексная форма записи уравнений соединений Имеем узел, к которому подключено п ветвей. По первому закону
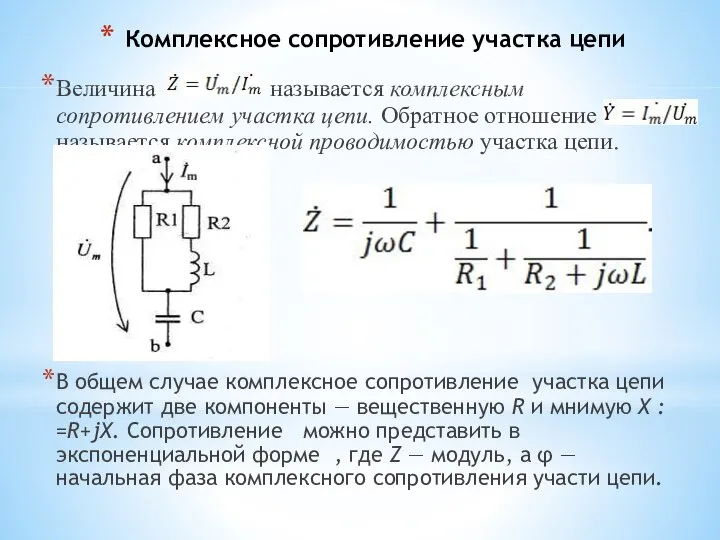
- 41. Комплексное сопротивление участка цепи Величина называется комплексным сопротивлением участка цепи. Обратное отношение называется комплексной проводимостью участка
- 42. 4. Мгновенная, активная, полная и реактивная мощность Минимальные и максимальные мощности принимаемого и передаваемого сигналов —
- 43. Баланс мощностей Для схемы, изображенной на рисунке, полная комплексная мощность источника равна Полная комплексная мощность двухполюсника
- 44. Лекция № 3. Сложные электрические цепи. Методы анализа 1. Некоторые особенности анализа сложных цепей 2. Метод
- 45. 1. Некоторые особенности анализа сложных цепей Метод токов ветвей основан на применении законов Кирхгофа. Имеем схему,
- 46. ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ Применение Закона Ома для участка цепи, не содержащего источник э.д.с.
- 47. Закон Ома для участка цепи, содержащего источник э.д.с.
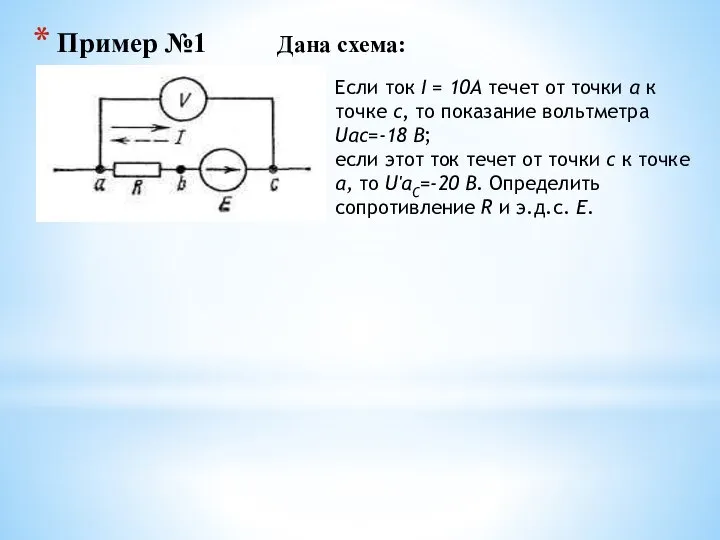
- 48. Пример №1 Дана схема: Если ток I = 10А течет от точки а к точке с,
- 49. Решение. В первом режиме Uac=-18=-Е+IR=-Е+10R, Во втором U'ac=-20=-Е-IR=-Е-10R. Совместное решение дает E=19 В, R=0,1 Ом.
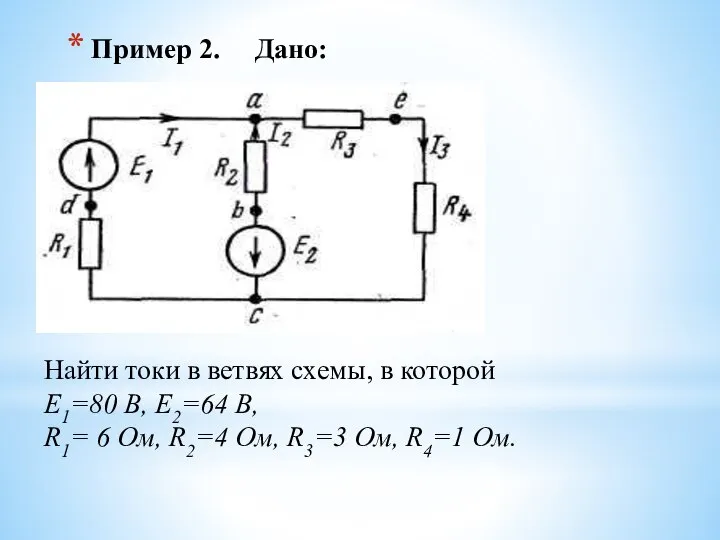
- 50. Пример 2. Дано: Найти токи в ветвях схемы, в которой Е1=80 В, Е2=64 В, R1= 6
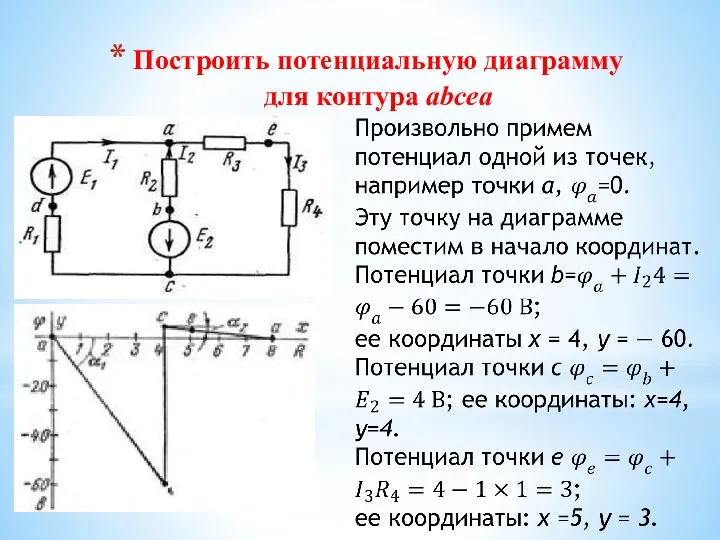
- 52. Потенциальная диаграмма Под потенциальной диаграммой понимают график распределения потенциала вдоль какого-либо участка цепи или замкнутого контура.
- 53. Построить потенциальную диаграмму для контура abcea
- 54. 2. Метод узловых напряжений Метод узловых напряжений (потенциалов) используется в программах машинного моделирования электронных схем. Метод
- 55. 3. Метод контурных токов Полагаем, что в каждом независимом контуре течет свой контурный ток. Контурный ток
- 56. 4. Свойства линейных цепей Выражение принципа суперпозиции (принципа наложения) По принципу дуальности, в соответствии с которым
- 57. Лекция № 4. Четырехполюсники, фильтры и длинные линии 1. Четырехполюсники 2. Электрические фильтры как четырехполюсники 3.
- 58. 1. Четырехполюсники Определение. Четырехполюсник — это устройство, имеющее четыре контакта: два входных контакта используются для подключения
- 59. Y-форма: H-форма: А-форма G-форма В-форма Y11 — входная проводимость при КЗ на выходе, Y12 — проводимость
- 60. Функции четырехполюсника: Ки=U2/U1 — комплексный коэффициент передачи по напряжению, Кр=Pвых/Pвх — коэффициент передачи активной мощности, Ki=I2/I1
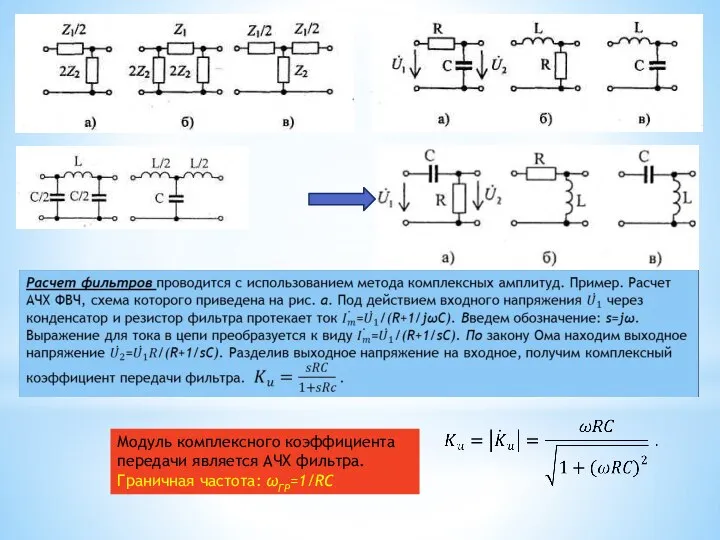
- 61. 2. Электрические фильтры как четырехполюсники Электрический фильтр — это устройство, предназначенное для пропускания сигналов только в
- 62. Фазочастотная характеристика (ФЧХ) ФЧХ определяется как начальная фаза (аргумент) комплексного коэффициента передачи фильтра: arg Классификация фильтров
- 63. Модуль комплексного коэффициента передачи является АЧХ фильтра. Граничная частота: ωГР=1/RC
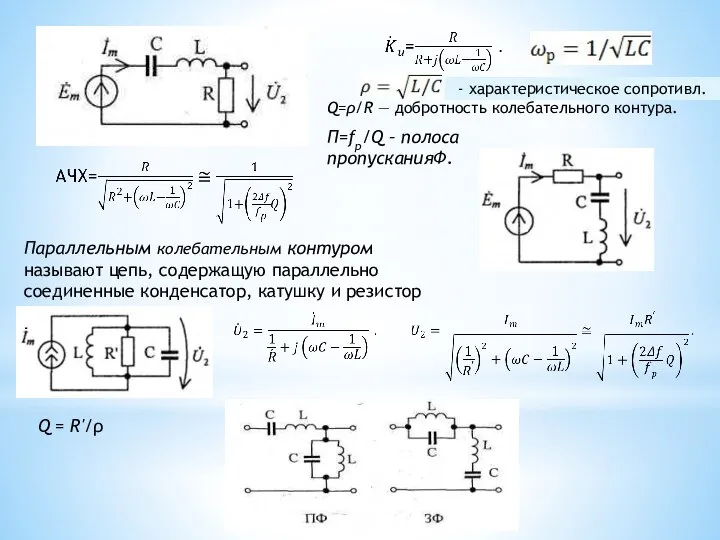
- 64. Q=ρ/R — добротность колебательного контура. Параллельным колебательным контуром называют цепь, содержащую параллельно соединенные конденсатор, катушку и
- 65. 3. Длинные линии и телеграфные уравнения В цепях с сосредоточенными параметрами все магнитные поля сосредоточены в
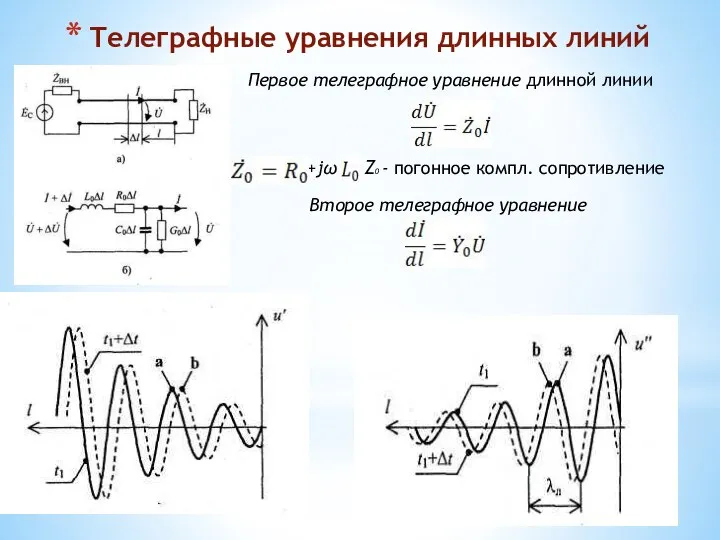
- 66. Телеграфные уравнения длинных линий Первое телеграфное уравнение длинной линии +jω Z0 - погонное компл. сопротивление Второе
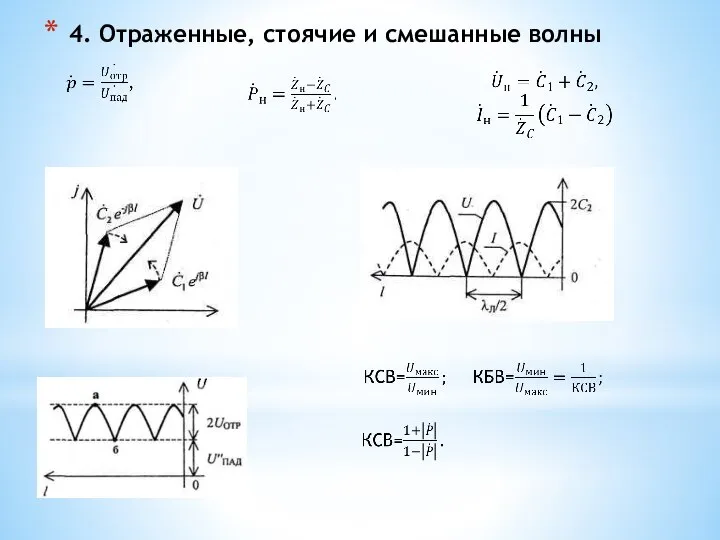
- 67. 4. Отраженные, стоячие и смешанные волны
- 68. СВЧ устройства Полосковая резонансная система
- 69. Примеры полосковых систем
- 70. Типы коаксиальных кабелей
- 79. Скачать презентацию

















































 Инфразвук и ультразвук
Инфразвук и ультразвук Техническое обслуживание и текущий ремонт сцепления, коробки передач, карданной передачи
Техническое обслуживание и текущий ремонт сцепления, коробки передач, карданной передачи 2_Dinamika
2_Dinamika Основы технической гидромеханики
Основы технической гидромеханики Открытие нейтрона
Открытие нейтрона Классификация тепловых двигателей
Классификация тепловых двигателей Свободные и вынужденные колебания. Колебательные системы. (9 класс)
Свободные и вынужденные колебания. Колебательные системы. (9 класс) Теория основных тепловых процессов химической технологии. Тепловой баланс. Промышленные теплоносители. Теплопроводность
Теория основных тепловых процессов химической технологии. Тепловой баланс. Промышленные теплоносители. Теплопроводность Организация технического обслуживания и текущего ремонта технологических машин
Организация технического обслуживания и текущего ремонта технологических машин Электрические силы
Электрические силы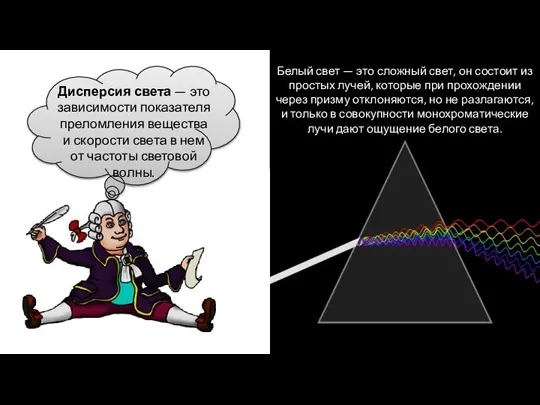 Дисперсия света
Дисперсия света Ядерная геофизика
Ядерная геофизика Резистор. Функциональное назначение резистра
Резистор. Функциональное назначение резистра Контрольная работа №5. Решения
Контрольная работа №5. Решения Презентация на тему Взаимодействие токов. Магнитное поле. Вектор магнитной индукции. Линии магнитной индукции
Презентация на тему Взаимодействие токов. Магнитное поле. Вектор магнитной индукции. Линии магнитной индукции  Демонстрационный вариант контрольных измерительных материалов единого государственного экзамена 2014 года по физике
Демонстрационный вариант контрольных измерительных материалов единого государственного экзамена 2014 года по физике Тест КПП автомобиля
Тест КПП автомобиля АЭС_1663630896
АЭС_1663630896 Основные Законы Природы
Основные Законы Природы Классическое определение вероятности Решение задач.
Классическое определение вероятности Решение задач. Сила Лоренца. Действие магнитного поля на движущуюся заряженную частицу
Сила Лоренца. Действие магнитного поля на движущуюся заряженную частицу Собственный механический и магнитный моменты электрона. Спин
Собственный механический и магнитный моменты электрона. Спин Конструкционные материалы. Классификация. Свойства
Конструкционные материалы. Классификация. Свойства Необыкновенные оптические явления
Необыкновенные оптические явления Определение электромагнитного поля. Практическое занятие
Определение электромагнитного поля. Практическое занятие Молекулярно-кинетическая теория
Молекулярно-кинетическая теория Консультация ГИА-9 по физике
Консультация ГИА-9 по физике Физическая величина
Физическая величина