Содержание
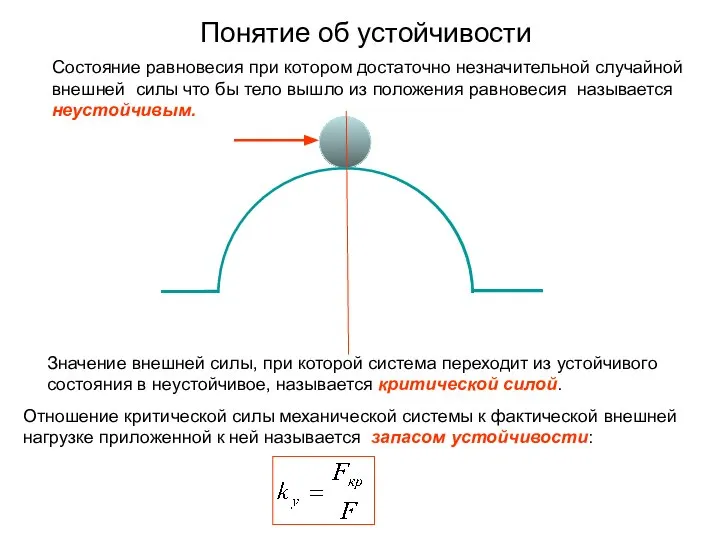
- 2. Понятие об устойчивости Состояние равновесия при котором достаточно незначительной случайной внешней силы что бы тело вышло
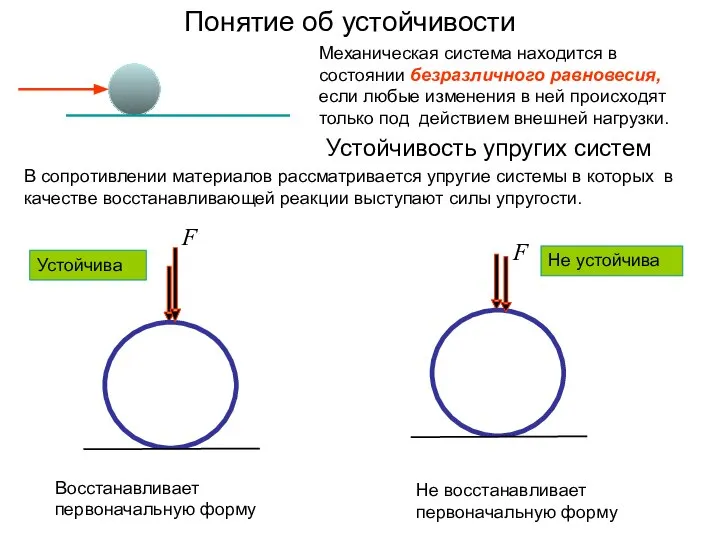
- 3. Понятие об устойчивости Не восстанавливает первоначальную форму Восстанавливает первоначальную форму Устойчивость упругих систем Механическая система находится
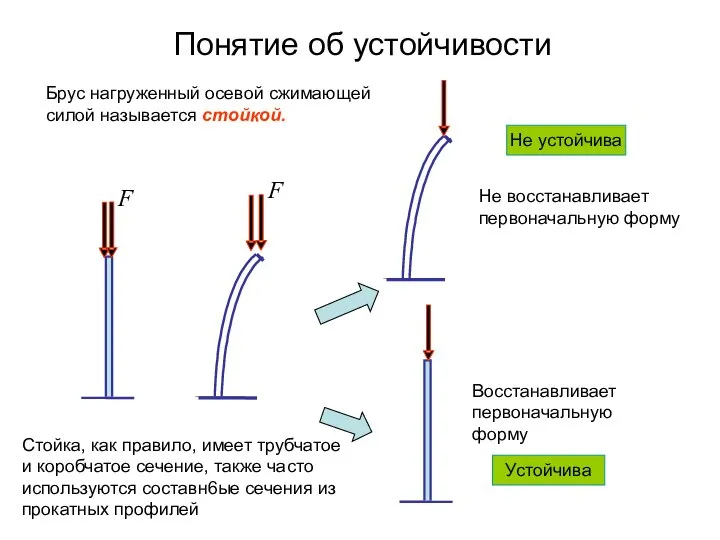
- 4. Понятие об устойчивости Устойчива Не устойчива Не восстанавливает первоначальную форму Восстанавливает первоначальную форму Брус нагруженный осевой
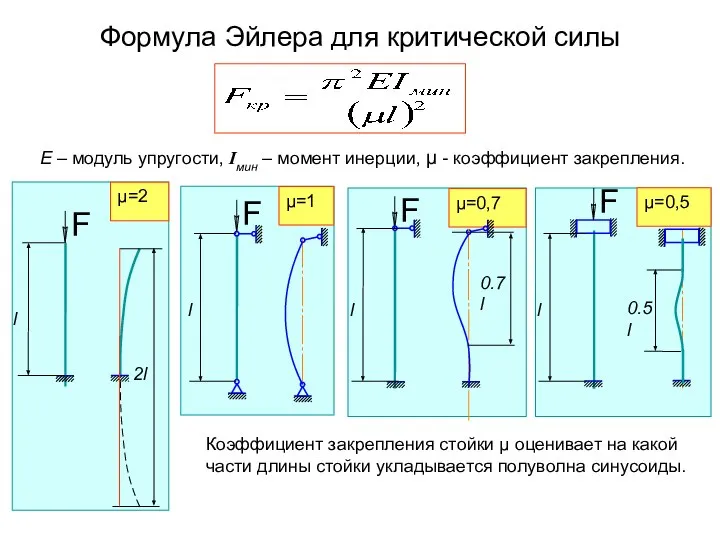
- 5. Формула Эйлера для критической силы μ=2 μ=0,7 μ=0,5 Е – модуль упругости, Iмин – момент инерции,
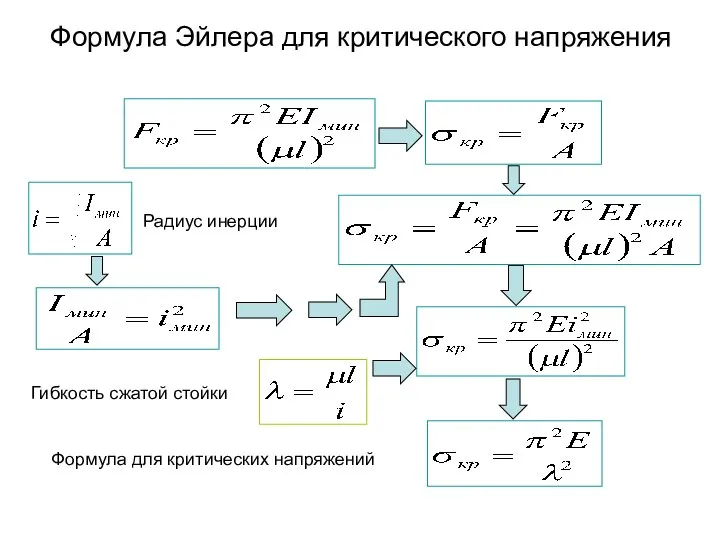
- 6. Формула Эйлера для критического напряжения Радиус инерции Гибкость сжатой стойки Формула для критических напряжений
- 7. Пределы применимости формулы Эйлера Формула Эйлера применима при условии если напряжения не превышают пределе пропорциональности σпц
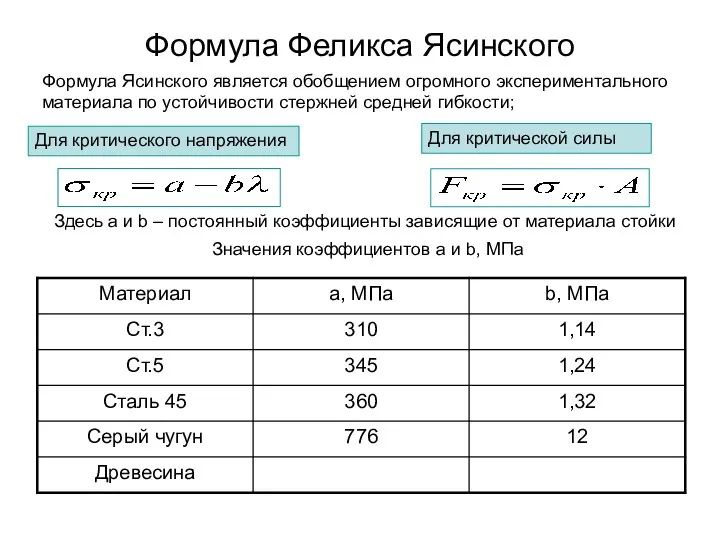
- 8. Формула Феликса Ясинского Для критической силы Для критического напряжения Здесь a и b – постоянный коэффициенты
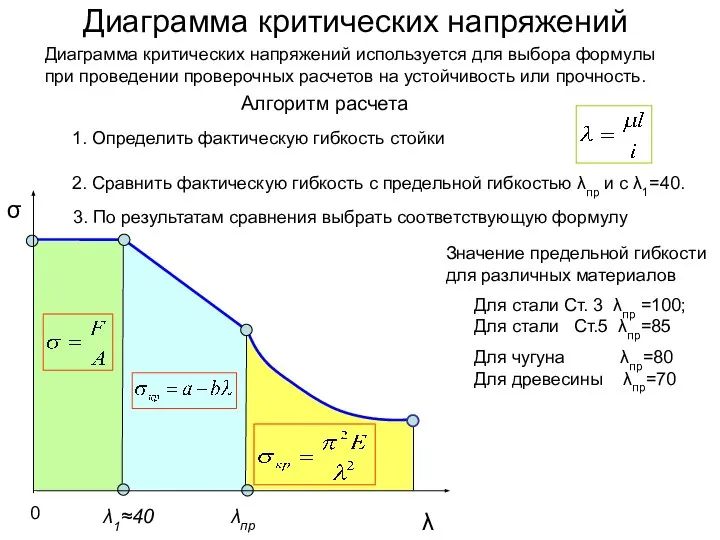
- 9. Диаграмма критических напряжений Для стали Ст. 3 λпр =100; Для стали Ст.5 λпр=85 Для чугуна λпр=80
- 10. Инженерный способ расчета на устойчивость Формулы Эйлера и Ясинского используются для выполнения проверочных расчетов конструкций на
- 11. Инженерный способ расчета на устойчивость 5. Фактическая гибкость стойки: 3. Геометрические размеры поперечного сечения 4. Радиус
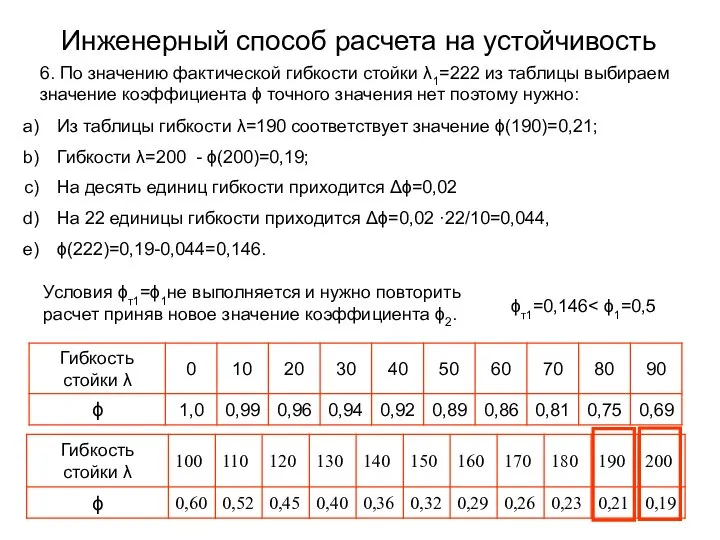
- 12. Инженерный способ расчета на устойчивость 6. По значению фактической гибкости стойки λ1=222 из таблицы выбираем значение
- 13. Инженерный способ расчета на устойчивость 11. Фактическая гибкость стойки: 9. Геометрические размеры поперечного сечения 10. Радиус
- 15. Скачать презентацию




 Колебательный контур
Колебательный контур Теория движения военных колесных машин. Лекция 4
Теория движения военных колесных машин. Лекция 4 Презентация на тему Задачи на движение
Презентация на тему Задачи на движение  Презентация на тему Воздухоплавание
Презентация на тему Воздухоплавание  Вычислительные методы механики деформируемого тела
Вычислительные методы механики деформируемого тела Подвеска автомобиля
Подвеска автомобиля Классификация подъёмников для автомобилей в СТО
Классификация подъёмников для автомобилей в СТО Механическое движение. Урок физики в 7 классе
Механическое движение. Урок физики в 7 классе Презентация на тему Световые кванты
Презентация на тему Световые кванты  Магнитное поле. Магнитостатика. Электромагнетизм
Магнитное поле. Магнитостатика. Электромагнетизм Применение бегущих волн в определении поврежденности интерфейсов в слоистых композитах
Применение бегущих волн в определении поврежденности интерфейсов в слоистых композитах Решение задач по теме Равновесие твердых тел
Решение задач по теме Равновесие твердых тел Курсовое проектирование на кафедре СМ-10 Колесные машины. Групповые консультации
Курсовое проектирование на кафедре СМ-10 Колесные машины. Групповые консультации Радиоактивные превращения. Экспериментальные методы исследования частиц
Радиоактивные превращения. Экспериментальные методы исследования частиц Колёсные часы. Маятниковые часы
Колёсные часы. Маятниковые часы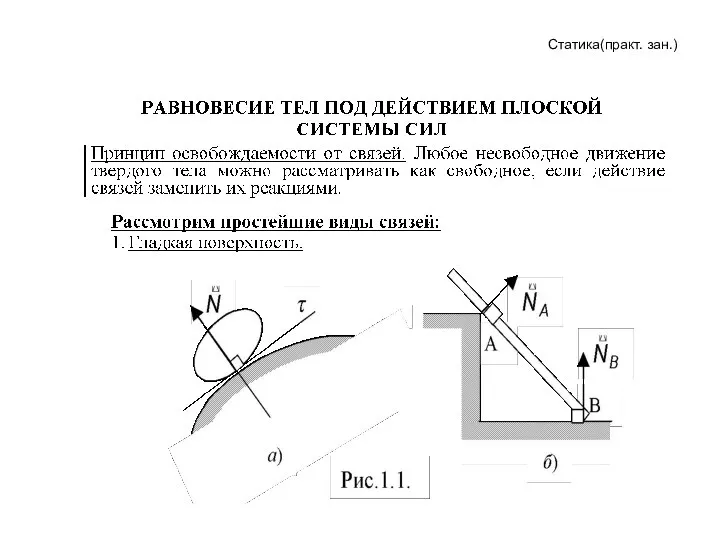 Равновесие тел под действием плоской системы сил
Равновесие тел под действием плоской системы сил Потери давления при движении потоков двухфазных
Потери давления при движении потоков двухфазных Геометрическая оптика
Геометрическая оптика Все о нагрузках. Практическое занятие
Все о нагрузках. Практическое занятие Демонстрационный вариант контрольных измерительных материалов для проведения в 2014 году государственной аттестации по физике
Демонстрационный вариант контрольных измерительных материалов для проведения в 2014 году государственной аттестации по физике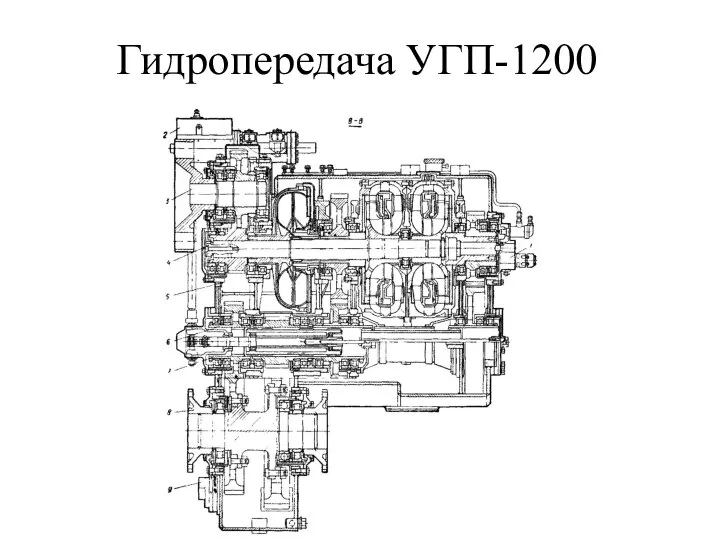 Гидропередача УГП-1200. Назначение, устройство и работа гидронасосов. Питательный насос
Гидропередача УГП-1200. Назначение, устройство и работа гидронасосов. Питательный насос Фотоэффект. Применение фотоэффекта
Фотоэффект. Применение фотоэффекта Технологии беспроводной передачи энергии методом электромагнитной индукции
Технологии беспроводной передачи энергии методом электромагнитной индукции Модернизация выжигателя
Модернизация выжигателя Что явилось причиной движения тела?
Что явилось причиной движения тела? Измерительный прибор для определения влажности воздуха - гигрометр
Измерительный прибор для определения влажности воздуха - гигрометр История и перспективы развития робототехники
История и перспективы развития робототехники Изобретения радио А.С. Поповым
Изобретения радио А.С. Поповым