Содержание
- 2. Лекция 6 Плоское потенциальное движение
- 3. Сложение потенциальных потоков Если поток является результатом сложения двух потенциальных течений, то он также будет потенциальным.
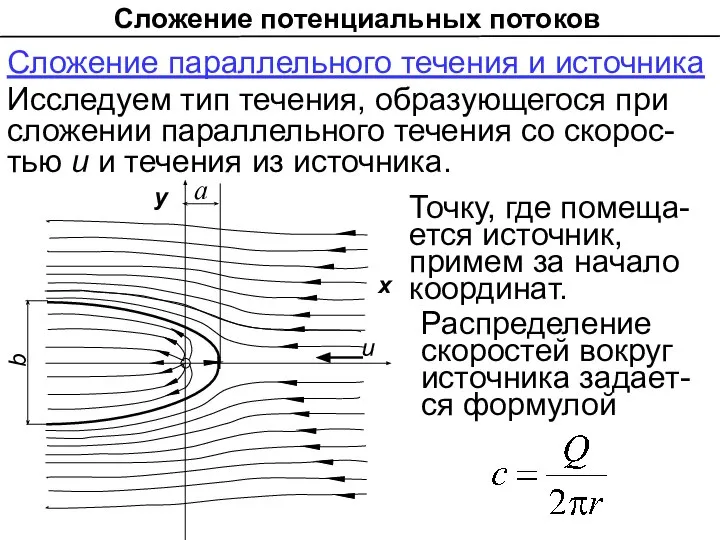
- 4. Сложение потенциальных потоков Сложение параллельного течения и источника Исследуем тип течения, образующегося при сложении параллельного течения
- 5. Сложение потенциальных потоков Легко показать, что на оси х течения должна существовать такая точка, в которой
- 6. Сложение потенциальных потоков Направление результирующих скоростей в точках, лежащих нa оси у определится формулой
- 8. Сложение потенциальных потоков Видно, что угол наклона этих скоростей к оси х, постоянно убывает с возрастанием
- 9. Сложение потенциальных потоков Уравнение Бернулли полностью остается в силе и после наложения двух течений. В бес-
- 10. Отсюда эта ширина b определяется уравнением: b ·и = Q; b = Q/и. К этой величине
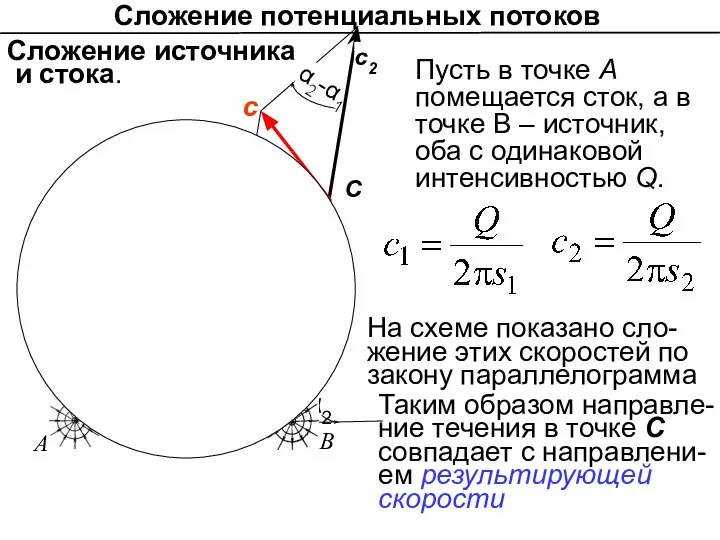
- 11. Сложение потенциальных потоков α1 s1 α2 α2-α1 α2-α1 s2 Пусть в точке А помещается сток, а
- 12. Сложение потенциальных потоков
- 13. Сложение потенциальных потоков Cкорость с направлена по касатeльной к окружности, проходящей через точки ABC. Окружность представляет
- 14. Сложение потенциальных потоков Диполь Если предположить, что источник и сток помещаются в одной точке, то с
- 15. Сложение потенциальных потоков Однако, можно рассматривать расстояние между источником и стоком l как бесконечно малую величину,
- 16. Сложение потенциальных потоков Эта пара «источник-сток» называется диполем. Произведение Q·l=М – момент диполя, а ось х
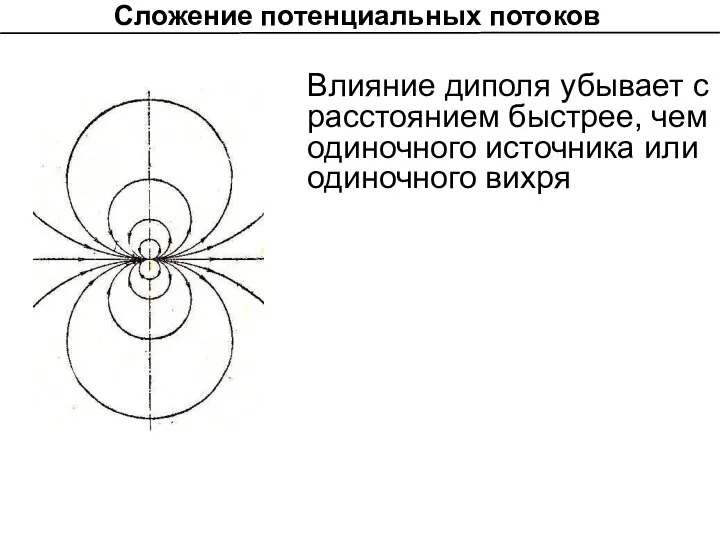
- 17. Сложение потенциальных потоков Влияние диполя убывает с расстоянием быстрее, чем одиночного источника или одиночного вихря
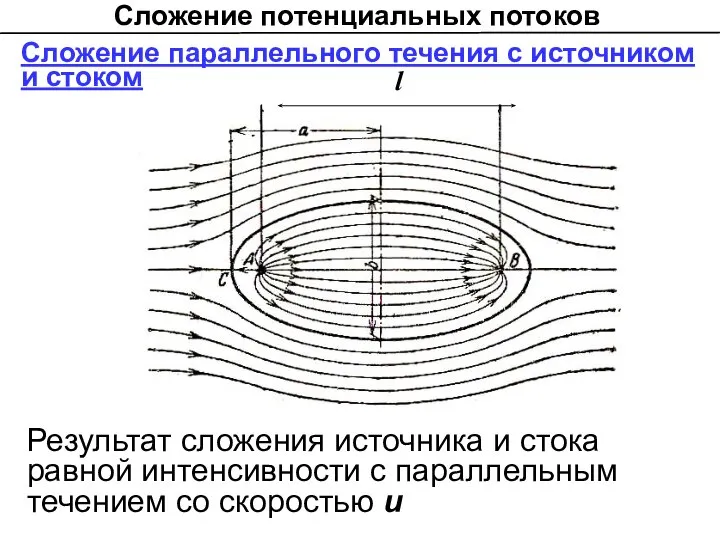
- 18. Сложение потенциальных потоков Сложение параллельного течения с источником и стоком l Результат сложения источника и стока
- 19. Влево от точки А скорость с пары источника и стока направлена противоположно скорости и . Так
- 20. Сложение потенциальных потоков Вторая критическая точка имеет абсциссу «-а». В этих границах будет теперь заключено все
- 21. Сложение потенциальных потоков Сложение источника и вихря Это суммарное течение называют вихреисточ-ником, если Q > 0,и
- 22. Сложение потенциальных потоков Угол α величина постоянная и, как можно ви-деть, точка, для которой определялась резуль-тирующая
- 24. Скачать презентацию

















 Бури. Скорость бури
Бури. Скорость бури Методы и приборы для измерения структурно-механических свойств пищевых продуктов
Методы и приборы для измерения структурно-механических свойств пищевых продуктов Устойчивость конструкций, механизмов
Устойчивость конструкций, механизмов О создании Комплекса NICA и необходимых расходах до 2022 года
О создании Комплекса NICA и необходимых расходах до 2022 года Теоретическая механика. Лекция 2. Связи и реакции связей
Теоретическая механика. Лекция 2. Связи и реакции связей Законы природы, проявления законов
Законы природы, проявления законов Škoda Octavia. Кузов. Оборудование кузова
Škoda Octavia. Кузов. Оборудование кузова Проектирование компрессорных установок горных предприятий. Занятие 7
Проектирование компрессорных установок горных предприятий. Занятие 7 Порівняння швидкостей різних рухомих тіл
Порівняння швидкостей різних рухомих тіл Презентация на тему Электричество в доме (8 класс)
Презентация на тему Электричество в доме (8 класс)  Первичные и вторичные параметры длинной линии. Лекция Д1
Первичные и вторичные параметры длинной линии. Лекция Д1 Презентация на тему Строение атома Квантовая физика
Презентация на тему Строение атома Квантовая физика  Измерение механических величин
Измерение механических величин Презентация на тему Виды электростанций
Презентация на тему Виды электростанций  Движение и силы
Движение и силы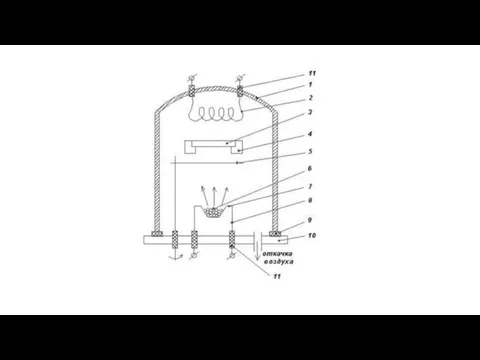 Физико-химические основы термического вакуумного напыления тонких пленок. Тема 8
Физико-химические основы термического вакуумного напыления тонких пленок. Тема 8 Сила тока. Напряжение
Сила тока. Напряжение Презентация на тему Исаак Ньютон
Презентация на тему Исаак Ньютон  Тормозные системы
Тормозные системы Электрическое поле
Электрическое поле Теория автоматического управления. Типовые звенья
Теория автоматического управления. Типовые звенья Физика атома и атомного ядра
Физика атома и атомного ядра Техническая механика. Раздел: Теоретическая механика. Лекция 1
Техническая механика. Раздел: Теоретическая механика. Лекция 1 Газовые законы
Газовые законы High-speed Machining
High-speed Machining Условия воспламенения и горения газов
Условия воспламенения и горения газов Уравнение плоской гармонической волны
Уравнение плоской гармонической волны Примеры теплопередач в природе, быту и технике
Примеры теплопередач в природе, быту и технике