Содержание
- 2. Силы и системы сил Сила — мера механического воздействия одного тела на другое. Физическая природа сил
- 3. Силы могут быть приложены при непосредственном контакте, так и за счет поля, в данном случае сила
- 4. Если на тело действует не одна сила, а несколько сил, то говорят о системе сил, действующих
- 5. Распределенная система сил – это система сил, когда точки приложения силы распределены по некоторой линии или
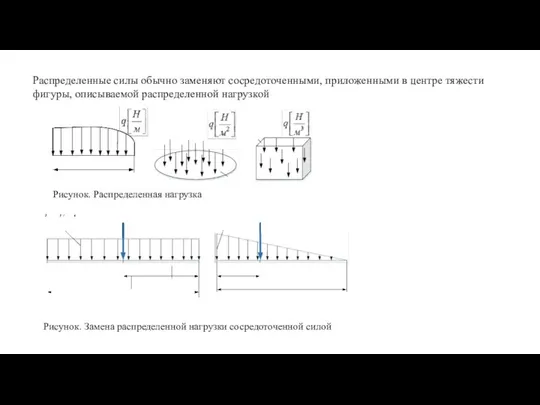
- 6. Распределенные силы обычно заменяют сосредоточенными, приложенными в центре тяжести фигуры, описываемой распределенной нагрузкой Рисунок. Распределенная нагрузка
- 7. Пример уравновешенной системы сил – известные герои басни Крылова: лебедь, рак и щука.
- 8. Свойства простейших систем сил В аксиомах статики формулируются те простейшие и общие законы, которым подчиняются силы,
- 9. Аксиома 1. Аксиома двух сил
- 10. Аксиома 2. Аксиома эквивалентности систем сил Если среди действующих на тело сил есть взаимно уравновешивающие силы,
- 11. Следствие из аксиом 1 и 2 Силу можно переносить вдоль линии действия в другую точку данного
- 12. Аксиома 3. Аксиома параллелограмма сил Она утверждает, что силы, действующие на твердое тело, приложенные в одной
- 13. Аксиома 4. Аксиома двух тел (3-й закон Ньютона) Два тела действуют друг на друга с силами,
- 14. Аксиома 5. Аксиома затвердевания Если деформируемое тело находится в равновесии, то равновесие не нарушается при его
- 15. Связи и реакции связей Свободное тело – тело, которое может совершать из данного положения любые перемещения
- 16. Тело, стремясь под действием приложенных сил осуществить перемещение, которому препятствует связь, будет действовать на нее с
- 17. Степени свободы, число степеней свободы Движение материальных тел и точек в пространстве можно представить в виде
- 18. Основные виды связей и их реакции Гладкая поверхность (без трения) или опора (рис. 1.10): Такая поверхность
- 19. Основные виды связей и их реакции Идеальная нить (нить, шнур, цепь) Идеальной называется гибкая, невесомая и
- 20. Идеальный стержень. Идеальным называется невесомый, нерастяжимый стержень, на концах которого шарниры и между этими концами никакой
- 21. Шарнирно-неподвижная опора Неподвижными называются шарнирные опоры, в которых возможность линейного перемещения точки закрепления ограничивается во всех
- 22. Шарнирно-подвижная опора отличается от цилиндрического шарнира тем, что допускает перемещение в одном из направлений, в данном
- 23. Основные виды связей и их реакции Сферический шарнир не дает перемещаться телу ни в одном из
- 24. Подпятник: эта связь, аналогично сферическому шарниру, не дает перемещаться точке закрепления в нижнюю полуплоскость. Используются подпятники
- 25. Основные виды связей и их реакции Жесткая заделка. Жесткая заделка не дает не только перемещаться телу
- 26. Пространственные опоры и их реакции Вал, закрепленный в опорах: в точке A – подпятник (или стакан),
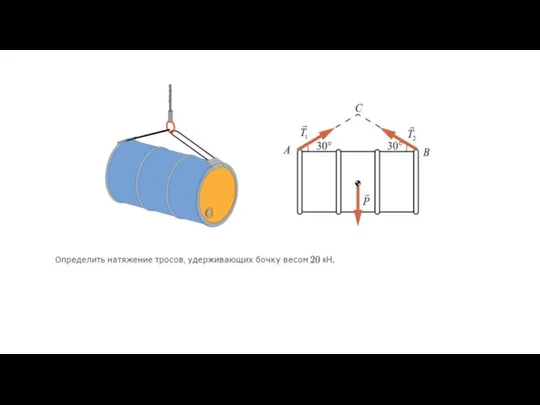
- 27. Сходящаяся система сил Сходящейся системой сил называется система сил, линии действия которых пересекаются в одной точке
- 28. Момент силы Момент силы – это мера вращательного действия силы, приложенного к телу, закрепленному в одной
- 29. Свойства момента сил относительно точки Момент силы относительно точки не изменится, если силу перенести вдоль линии
- 30. Пример: найти реакции ремня трансмиссионной передачи относительно оси y. Ось y – это ось вала, на
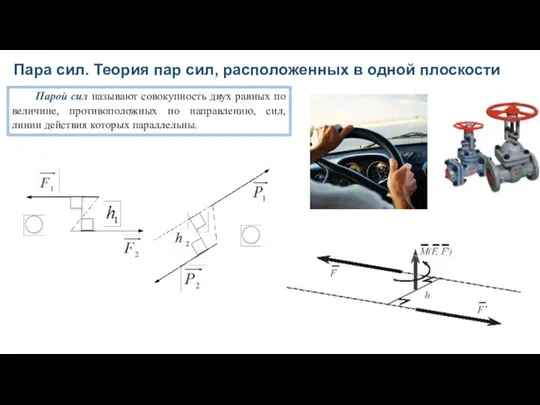
- 31. Пара сил. Теория пар сил, расположенных в одной плоскости Парой сил называют совокупность двух равных по
- 32. , Сила, равная геометрической сумме всех сил системы, называется главным вектором системы.
- 36. Условия равновесия произвольной пространственной системы сил Для равновесия произвольной пространственной системы сил необходимо и достаточно, чтобы
- 37. Равновесие системы параллельных сил Для равновесия системы параллельных сил необходимо и достаточно, чтобы сумма проекций этих
- 38. Равновесие плоской системы сил Для равновесия плоской системы сил необходимо и достаточно, чтобы сумма проекций этих
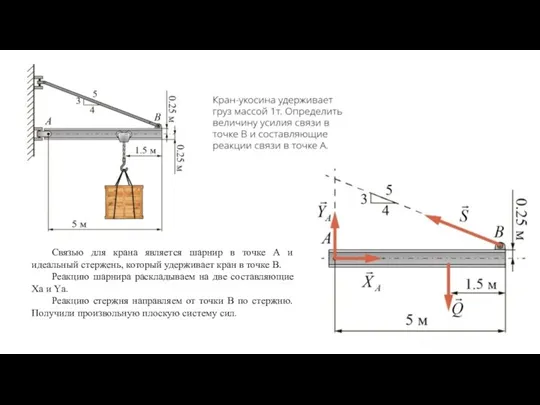
- 39. Связью для крана является шарнир в точке А и идеальный стержень, который удерживает кран в точке
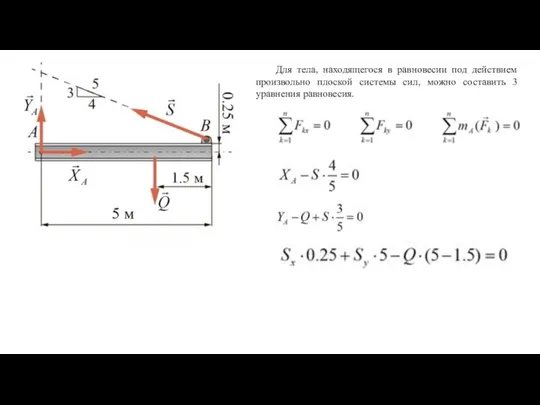
- 40. Для тела, находящегося в равновесии под действием произвольно плоской системы сил, можно составить 3 уравнения равновесия.
- 44. Скачать презентацию




































 Модель с силами сцепления у вершины трещины. Модель Дагдейла
Модель с силами сцепления у вершины трещины. Модель Дагдейла Большой адронный коллайдер - путь к апокалипсису или прогрессу?
Большой адронный коллайдер - путь к апокалипсису или прогрессу? Тайны мыльных пузырей
Тайны мыльных пузырей Презентация на тему Напряженность электростатического поля
Презентация на тему Напряженность электростатического поля  Схемный анализ ОЭП
Схемный анализ ОЭП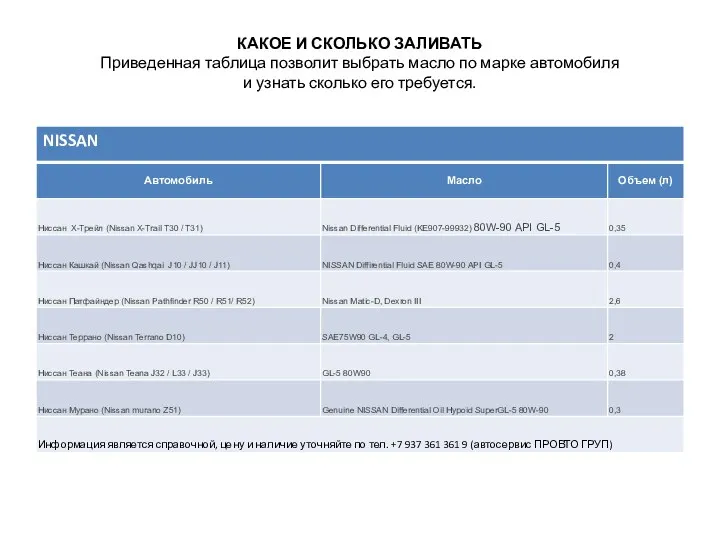 Объем заправочных масел
Объем заправочных масел Терагерцевое излучение
Терагерцевое излучение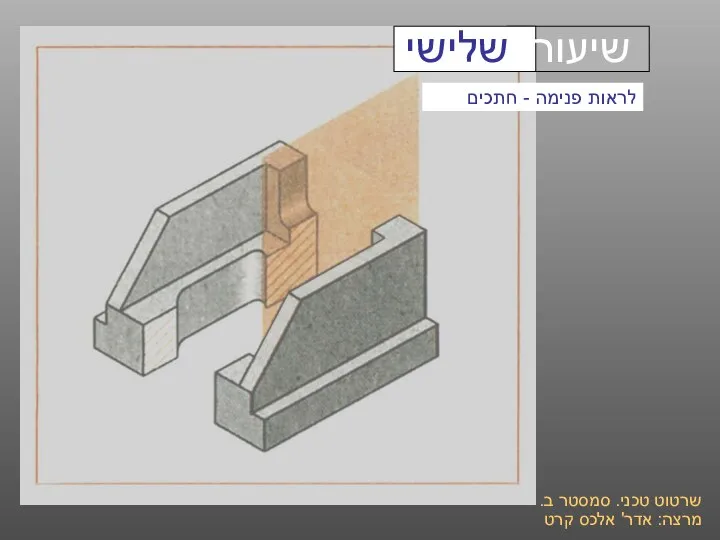 מצגת חתכים נוספת
מצגת חתכים נוספת Презентация на тему Механическая работа и мощность
Презентация на тему Механическая работа и мощность  Физические свойства жидкостей
Физические свойства жидкостей Исследователи света и цвета
Исследователи света и цвета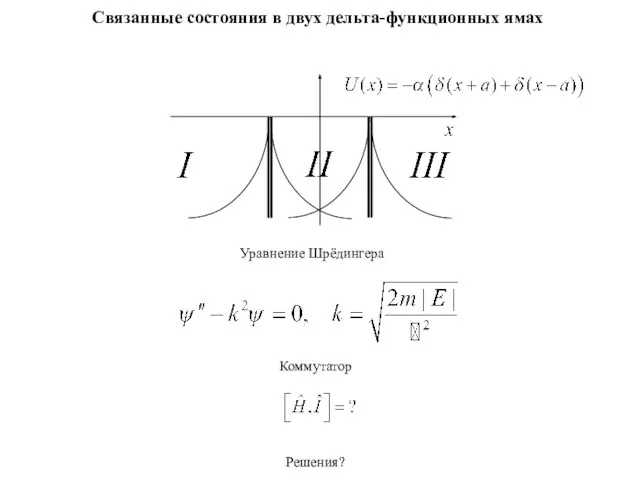 Связанные состояния в двух дельта - функционных ямах
Связанные состояния в двух дельта - функционных ямах Механическое движение
Механическое движение Прямолинейное распространение света
Прямолинейное распространение света Презентация на тему Изобретение радио А.С. Поповым
Презентация на тему Изобретение радио А.С. Поповым  Простейшие движения твердого тела
Простейшие движения твердого тела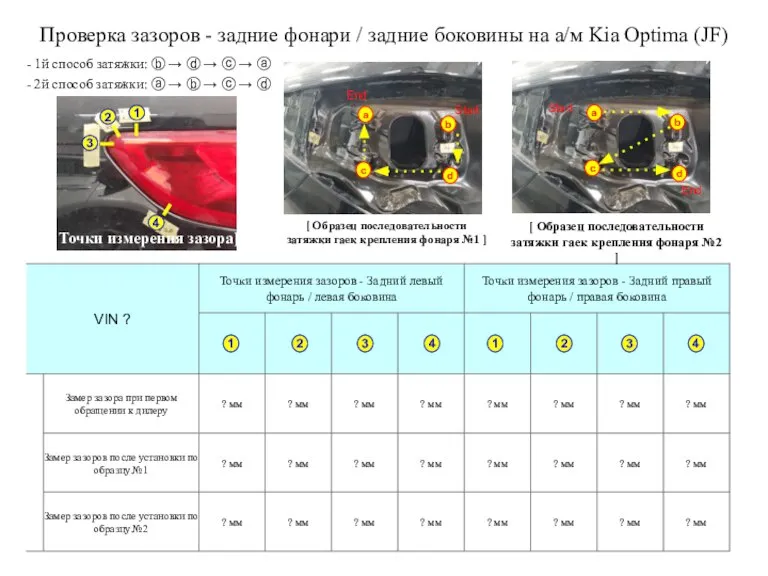 Проверка зазоров - задние фонари / задние боковины на а/м Kia Optima (JF)
Проверка зазоров - задние фонари / задние боковины на а/м Kia Optima (JF) Презентация 3
Презентация 3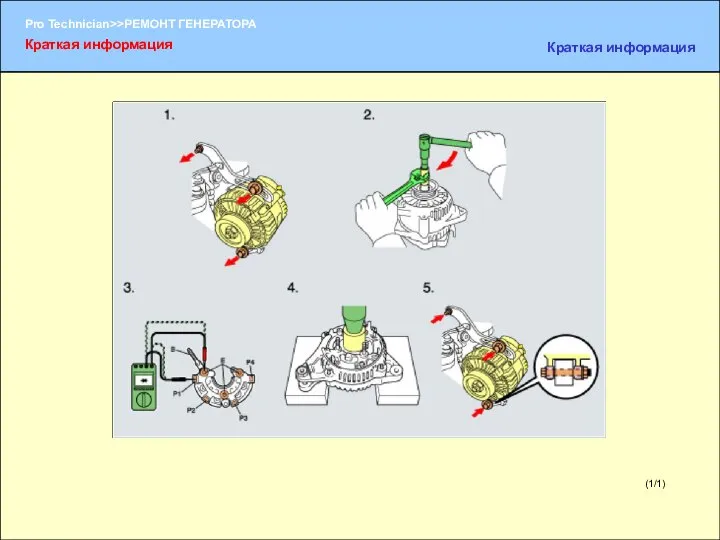 Ремонт генератора
Ремонт генератора Простые и сложные вещества
Простые и сложные вещества Прямолинейное равномерное и прямолинейное равноускоренное движения
Прямолинейное равномерное и прямолинейное равноускоренное движения Викторина по физике 9 класс
Викторина по физике 9 класс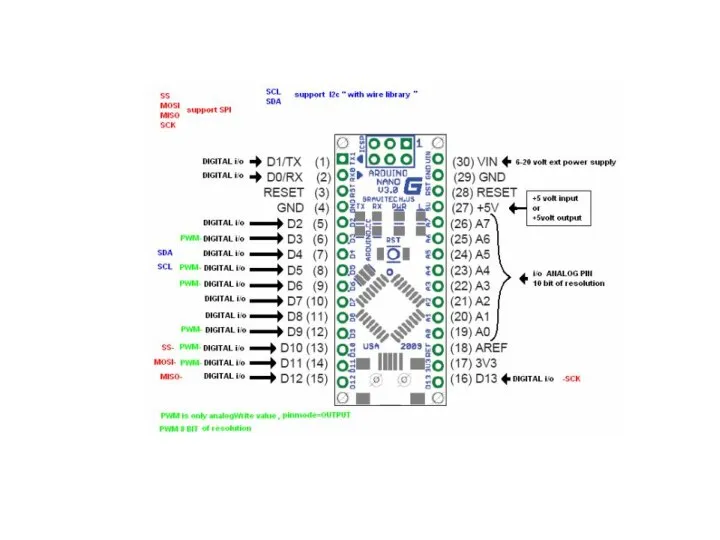 ЦАП Цифро-аналоговый преобразователь
ЦАП Цифро-аналоговый преобразователь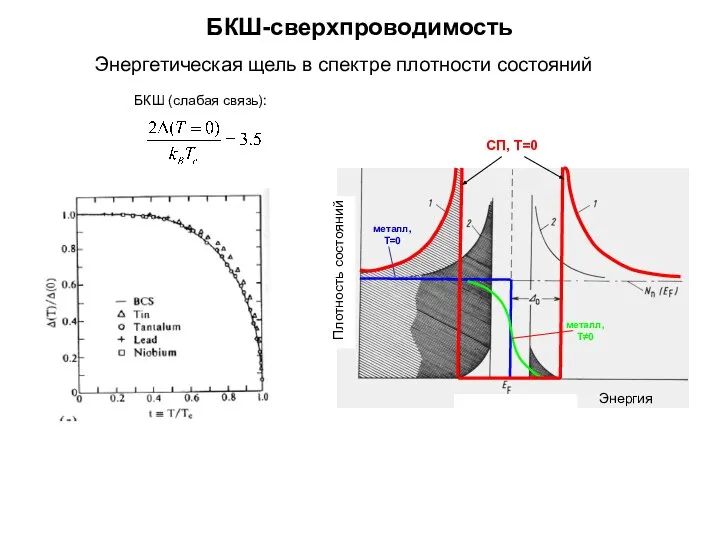 БКШ-сверхпроводимость. Терагерцовая оптика
БКШ-сверхпроводимость. Терагерцовая оптика Тепловые явления. Физическая величина
Тепловые явления. Физическая величина Линии влияния усилий в фермах
Линии влияния усилий в фермах Свободное падение тел, ускорение свободного падения
Свободное падение тел, ускорение свободного падения Презентация на тему Закон сохранения энергии
Презентация на тему Закон сохранения энергии