розвязування трикутників

Мета уроку:-
закріпити знання тригонометричних функцій гострого кута прямокутного трикутника,
-навчитися знаходити невідомі елементи прямокутного трикутника по відомих двом його елементам,
-застосовувати теоретичні знання для вирішення практичних завдань,
-удосконалювати уміння застосовувати теорему Піфагора при рішенні прикладних завдань;
- показати учням на прикладах її практичне вживання в повсякденному житті

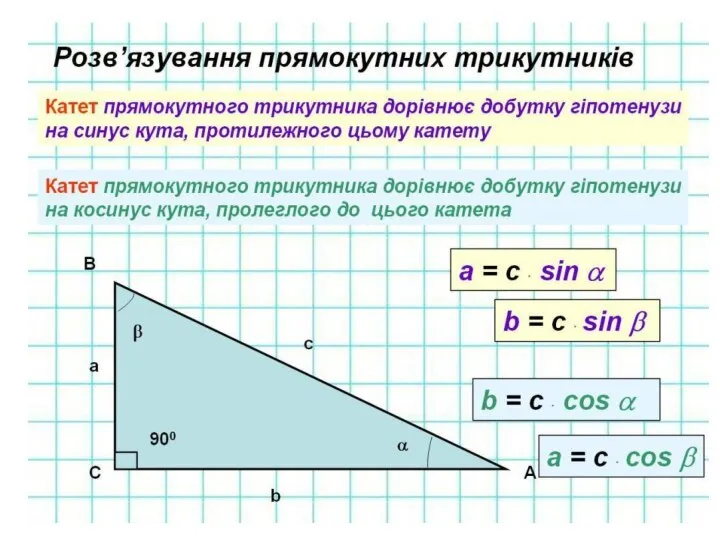
Вірю чи не вірю
1.У прямокутному трикутнику квадрат гіпотенузи дорівнює сумі квадратів катетів.

Вірю чи не вірю
2.Сума гострих кутів прямокутного трикутника дорівнює 180 градусів

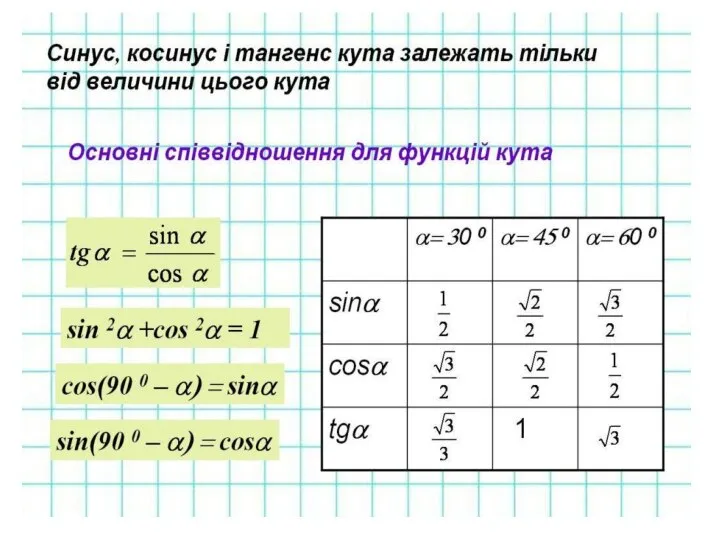
Вірю чи не вірю
3.Основна тригонометрична тотожність має вигляд:
sin2α + cos2α = 1

Вірю чи не вірю
4.Трикутник, у якого є прямий кут , називається гострокутним

Вірю чи не вірю
5.Сторона прямокутного трикутника, що лежить проти прямого кута, називається гіпотенуза

Вірю чи не вірю
6.Висота, проведена до гіпотенузи, ділить трикутник на три подібних трикутника

Вірю чи не вірю
7.Гіпотенуза більша за будь-який катет

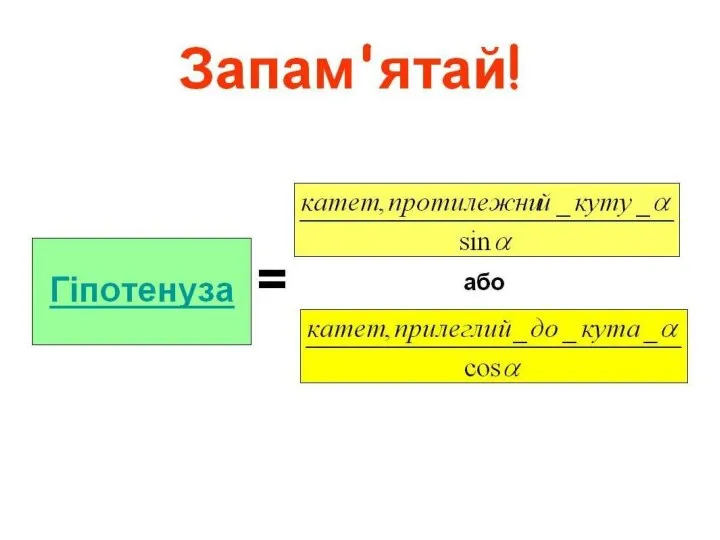
Вірю чи не вірю
8.Відношення протилежного катета до гіпотенузи в прямокутному трикутнику називається тангенсом кута

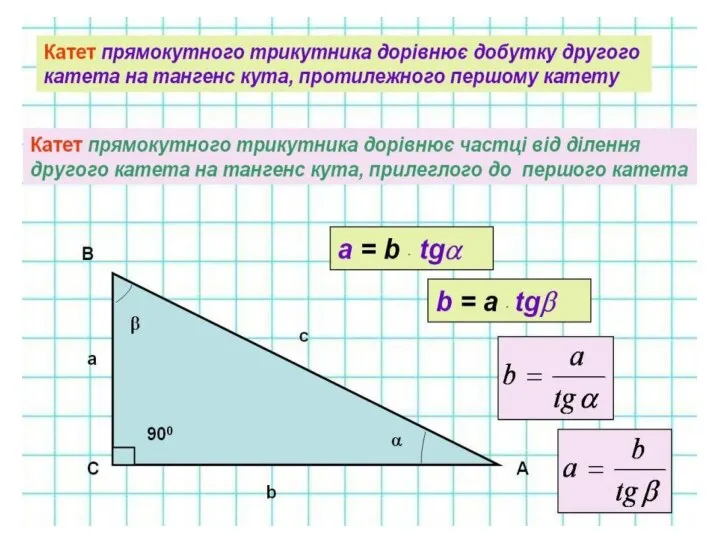
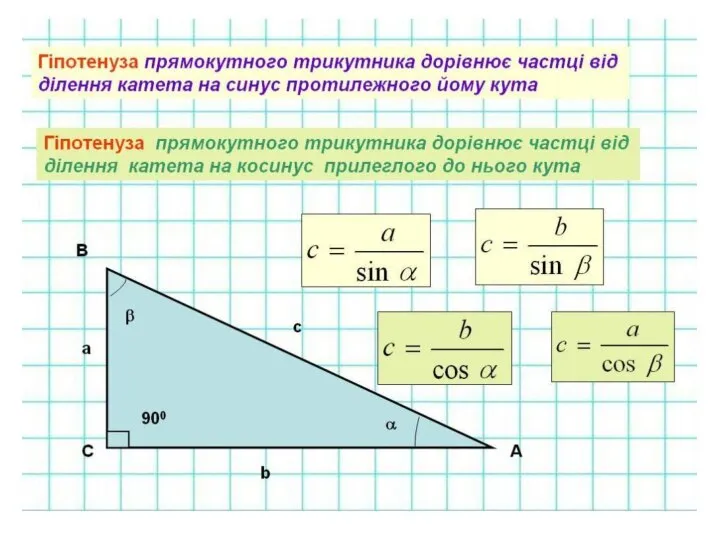
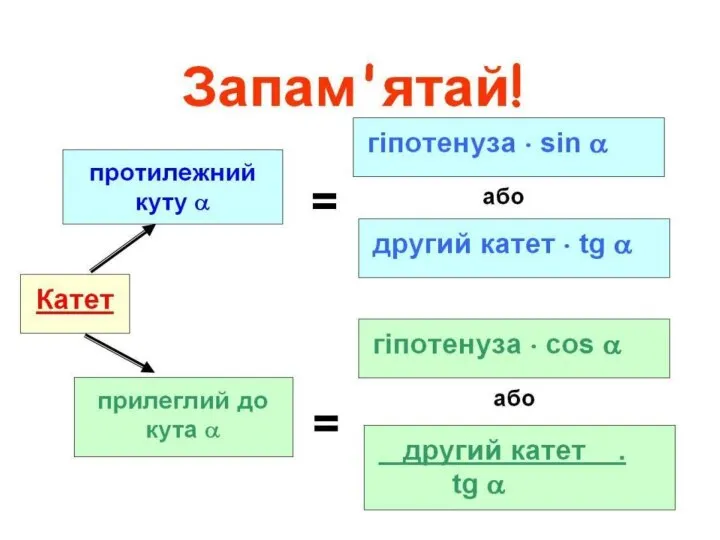
Вірю чи не вірю
9.Розв'язати прямокутний трикутник означає знайти його всі сторони і кути за відомими сторонами і кутами

Вірю чи не вірю
10. Чи дорівнює катет, який лежить проти кута 30° половині гіпотенузи

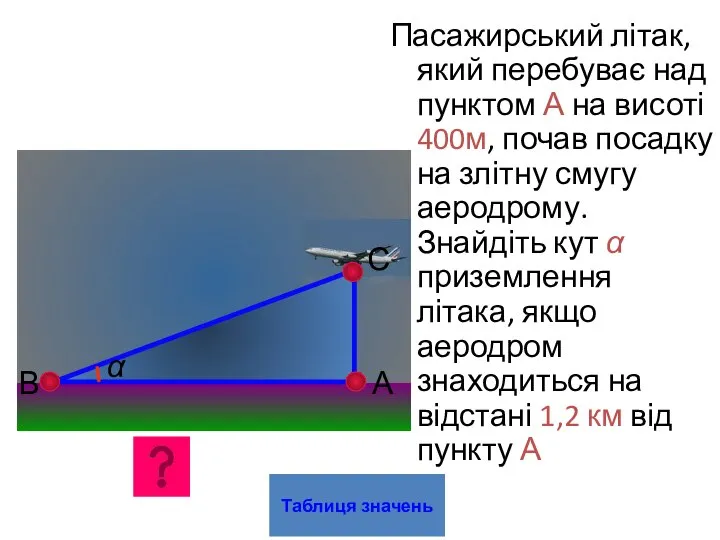
Пасажирський літак, який перебуває над пунктом А на висоті 400м, почав посадку на злітну смугу аеродрому. Знайдіть кут α приземлення літака, якщо аеродром знаходиться на відстані 1,2 км від пункту А
Таблиця значень

Розв’язання:
АС=400м
АВ=1,2км=1200м
tgα=FC:AB=400:1200=1/3=0,3333
α=18

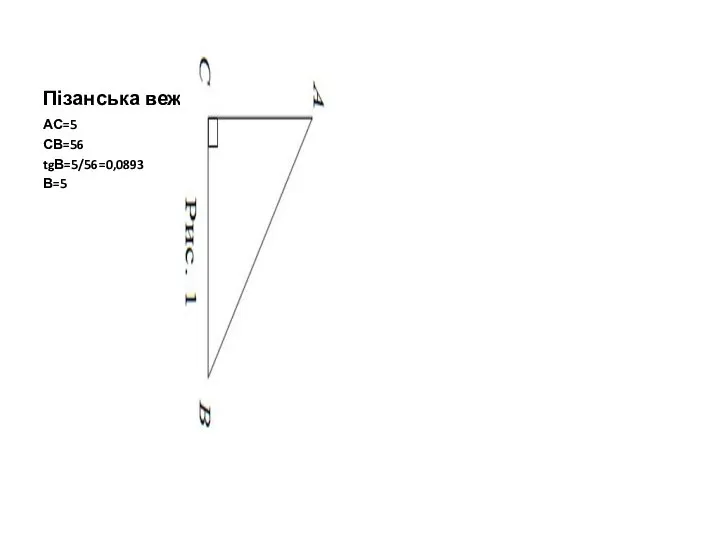
«Пізанська вежа»
Визначити кут нахилу вежі, якщо нам відома її висота – 56 м і те, що вершина вежі була відхилена на відстань приблизно 5 м від центру

Пізанська вежа
АС=5
СВ=56
tgВ=5/56=0,0893
В=5

Теодоліт
Теодоліт — прилад для вимірювання кутів (горизонтальних і вертикальних) на місцевості
.

Астролябія
Астролябія – стародавній кутомірний прилад для визначення широти і довжини в астрономо-геодезичних вимірах і навігації.

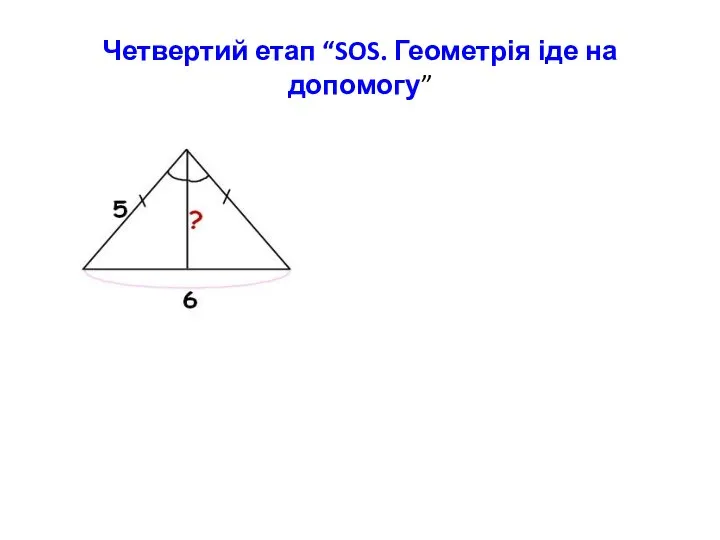
Четвертий етап “SOS. Геометрія іде на допомогу”

Бісектриса рівнобедреного трикутника ,проведена до основи,є і висотою, і медіаною. Н=√5²-3²=√16=4.

«Допомогла теорема Піфагора».
Якої довжини має бути драбина, щоб її можна було приставити до вікна, розташованого на висоті 150см, якщо відстань від нижнього кінця драбини до будинку має дорівнювати 200см?

«Допомогла теорема Піфагора»
Розв’язання:
АС=200см =2м, ВС=150см=1,5м.Тоді АВ=√2,25+4=2,5м.
Відповідь: 2,5м

«Допомогла теорема Піфагора».
Покажемо як можна довести за допомогою теореми Піфагора невинність або винність підозрюваного. Цей епізод узятий з реальної слідчої практики. Отримавши повідомлення про крадіжку Шерлок Холмс виїхав на місце випадку. Заявник стверджував, що злочинець проник в приміщення, де зберігалися цінності, через вікно. Огляд показав, що підвіконня знаходиться на відстані 150 см від землі. Поверхня землі на відстані 200 см від стіни будівлі покрита густою порослю, що не мала жодних слідів пошкоджень. При огляді не було знайдено жодних технічних засобів типа сходів. Виникло припущення, що злочинець проникав в приміщення через вікно, якимсь чином здолавши відстань між зовнішнім краєм поросли і підвіконням. Воно було визначене за допомогою теореми Піфагора

«Допомогла теорема Піфагора».
Висновок Шерлока: Слідчий висунув версію про інсценування кражі,бо драбини коло вікна не було,а перепригнути через кущі та допригнути до високого вікна не реально.

Допомога кораблю
АС=1150м
А=90-9=81
Знайти ВС
ВС=АСхsin81=
=1150х0,988=1136,2м
Відповідь: 1136,2м

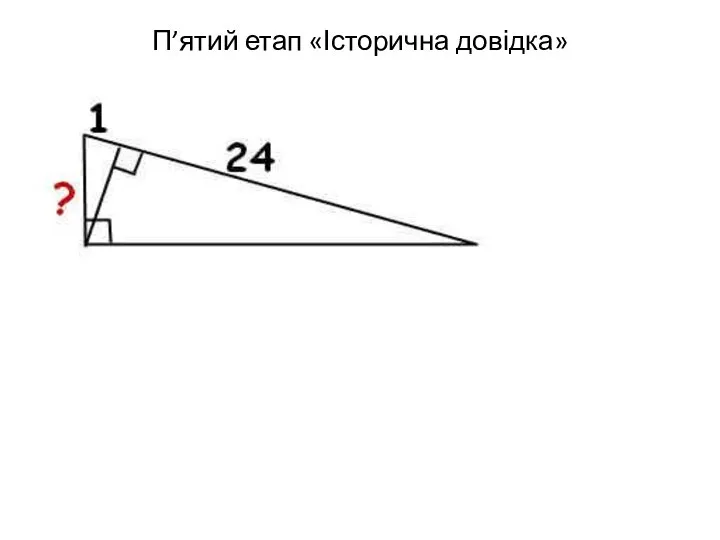
П’ятий етап «Історична довідка»

Катет є середнім пропорційним між гіпотенузою і проекцією катета на гіпотенузу.
с=24+1=25. а=√1х25=5.

Що найбільше запам’ятали на сьогоднішньому уроці?
Де ще можна застосовувати вивчений матеріал?
Закінчіть, будь ласка, речення:
Було цікаво.. працювати на уроці
Було складно... розв’язувати деякі задачі
Я виконував завдання... задоволенням чи ні
Я зрозумів ... зможу виконати вправи
Я запам’ятав…..