Содержание
- 2. Статикой называется раздел механики, в котором излагается общее учение о силах и изучаются условия равновесия материальных
- 3. Абсолютно твердое тело – это тело, которое ни при каких условиях не может деформироваться и любые
- 4. Сила как величина векторная характеризуется модулем, направлением в пространстве и точкой приложения Результат действия силы на
- 5. Точку приложения силы можно переносить только вдоль прямой, вдоль которой эта сила действует Сила, которая производит
- 6. Если к телу приложено две силы в одной точке, то равнодействующую находят по правилу параллелограмма Модуль
- 7. Если непараллельные силы приложены в разных точках тела, то для нахождения их равнодействующей эти силы и
- 8. Условие равновесия тела, не имеющего оси вращения Условие равновесия такого тела, как и условие равновесия материальной
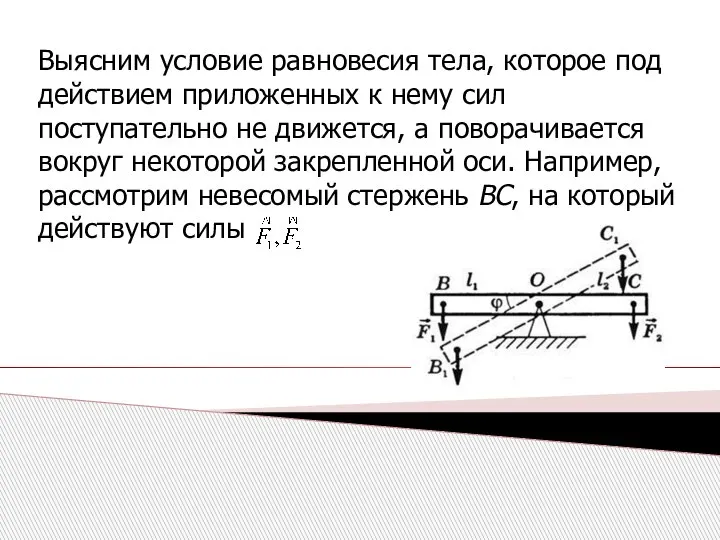
- 9. Выясним условие равновесия тела, которое под действием приложенных к нему сил поступательно не движется, а поворачивается
- 10. Повернем его на небольшой угол φ вокруг оси О. При этом точки приложения сил F⃗1 и
- 11. Эти силы совершают работу: Произведение силы на ее плечо называют моментом силы относительно оси вращения: Момент
- 12. Суммарная работа, совершаемая силами F1 и F2, составляет На основании теоремы о кинетической энергии ΔWk =
- 13. Условия равновесия твердого тела В общем случае, если тело под действием приложенных к нему сил может
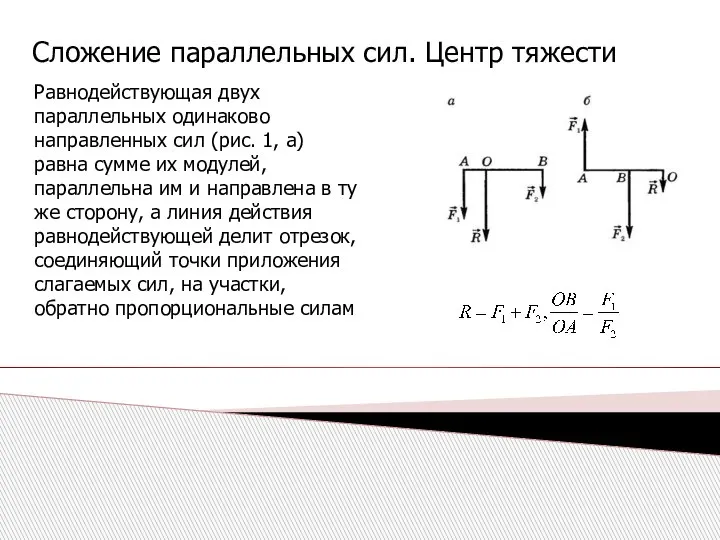
- 14. Сложение параллельных сил. Центр тяжести Равнодействующая двух параллельных одинаково направленных сил (рис. 1, а) равна сумме
- 15. Сложение параллельных сил. Центр тяжести Это можно доказать: если в предполагаемой точке О приложения равнодействующей мысленно
- 16. Равнодействующая двух антипараллельных сил (рис.1 , б) равна по модулю разности их модулей, параллельна им, направлена
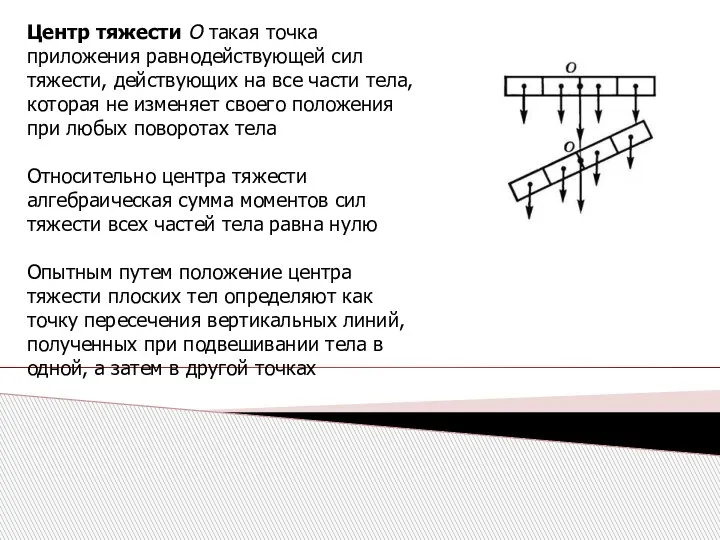
- 18. Центр тяжести О такая точка приложения равнодействующей сил тяжести, действующих на все части тела, которая не
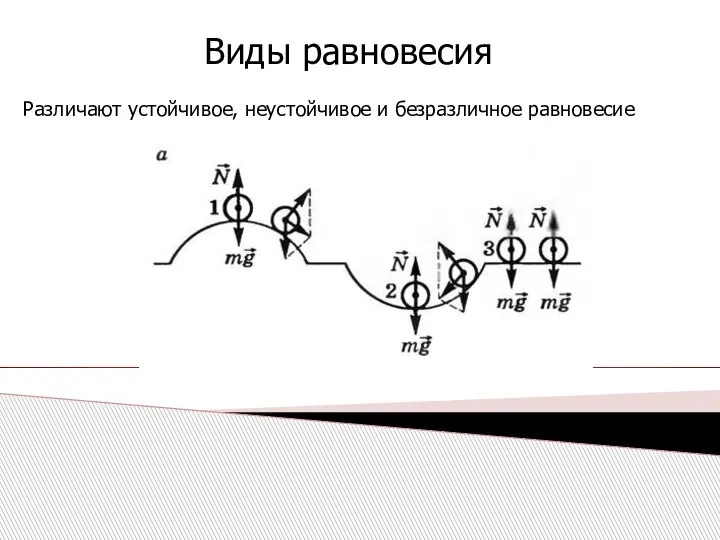
- 19. Виды равновесия Различают устойчивое, неустойчивое и безразличное равновесие
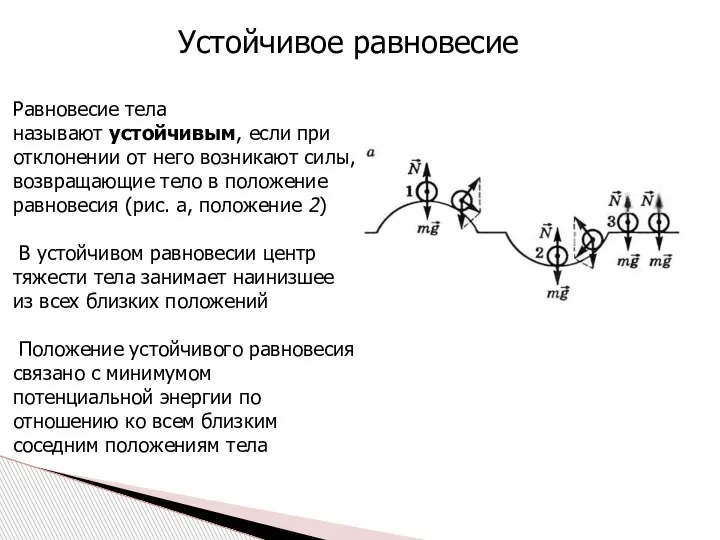
- 20. Равновесие тела называют устойчивым, если при отклонении от него возникают силы, возвращающие тело в положение равновесия
- 21. Равновесие тела называют неустойчивым, если при самом незначительном отклонении от него равнодействующая действующих на тело сил
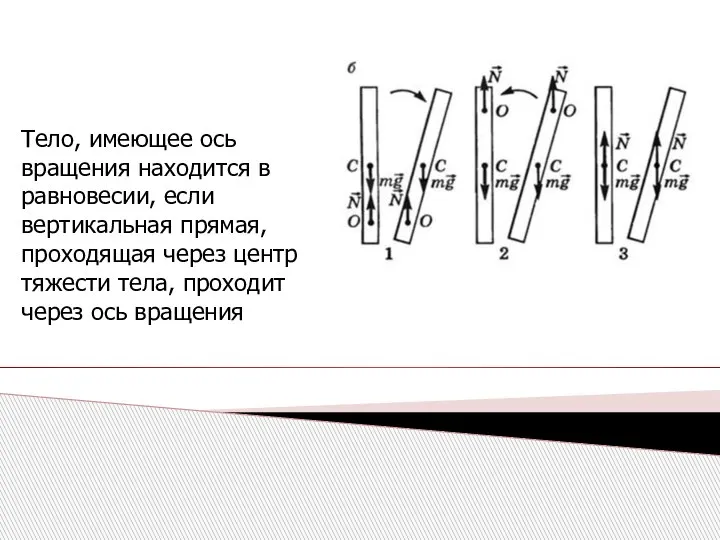
- 22. Тело, имеющее ось вращения находится в равновесии, если вертикальная прямая, проходящая через центр тяжести тела, проходит
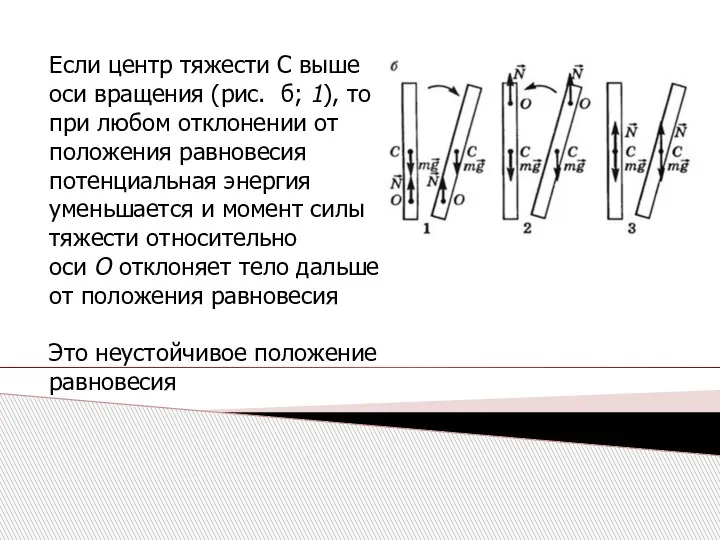
- 23. Если центр тяжести С выше оси вращения (рис. б; 1), то при любом отклонении от положения
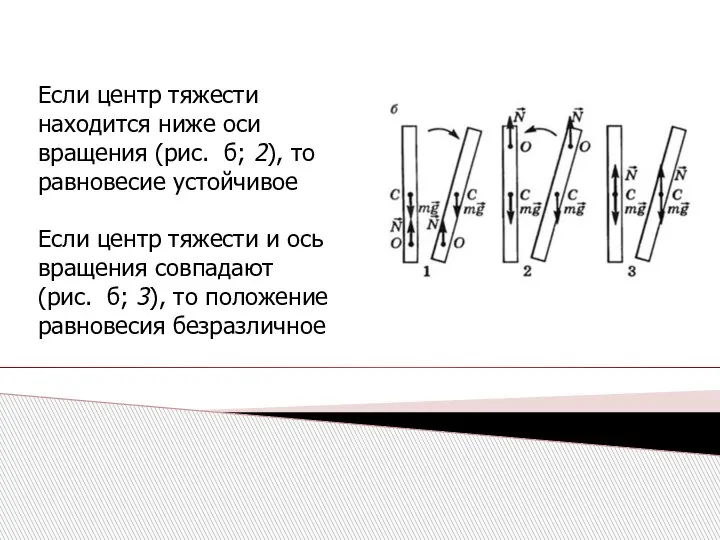
- 24. Если центр тяжести находится ниже оси вращения (рис. б; 2), то равновесие устойчивое Если центр тяжести
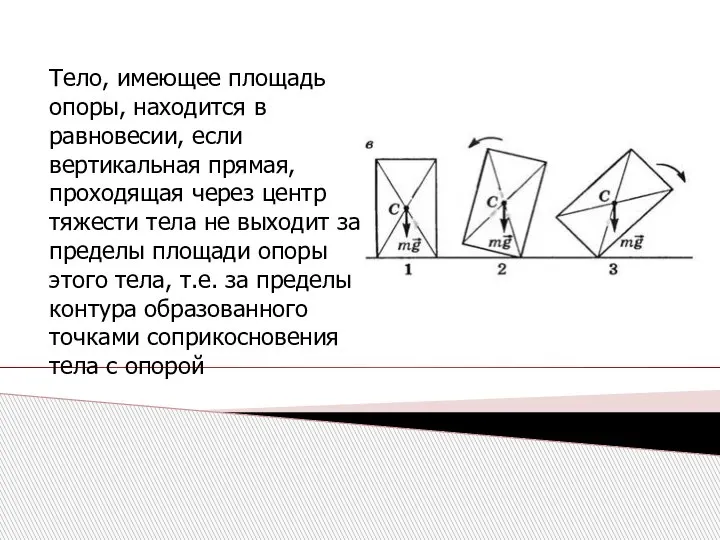
- 25. Тело, имеющее площадь опоры, находится в равновесии, если вертикальная прямая, проходящая через центр тяжести тела не
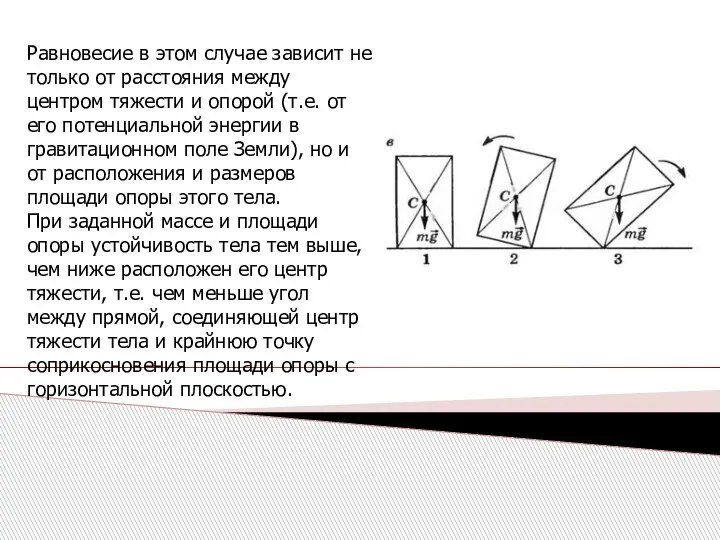
- 26. Равновесие в этом случае зависит не только от расстояния между центром тяжести и опорой (т.е. от
- 27. Простейшие механизмы Простые механизмы — это устройства, в которых работа совершается только за счет механической энергии.
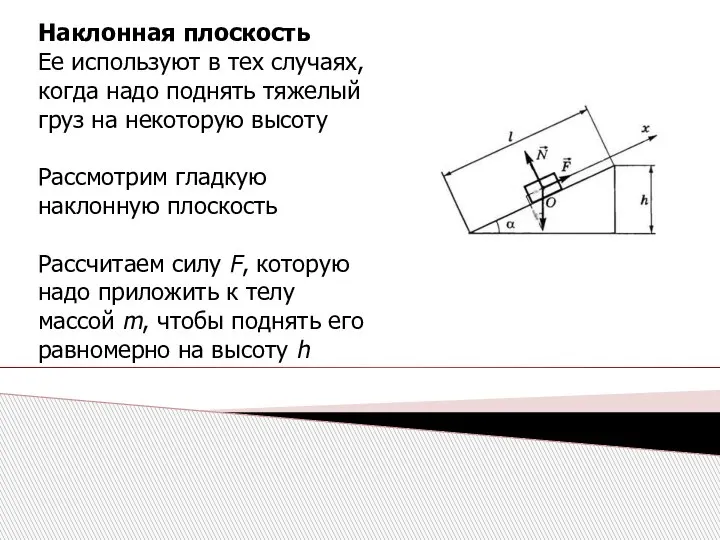
- 28. Наклонная плоскость Ее используют в тех случаях, когда надо поднять тяжелый груз на некоторую высоту Рассмотрим
- 29. Запишем основное уравнение динамики Отсюда искомая сила Спроецируем это равенство на ось Ox т.е для равномерного
- 30. Рычаг Рычагом называют имеющее неподвижную ось вращения твердое тело, на которое действуют силы, стремящиеся повернуть его
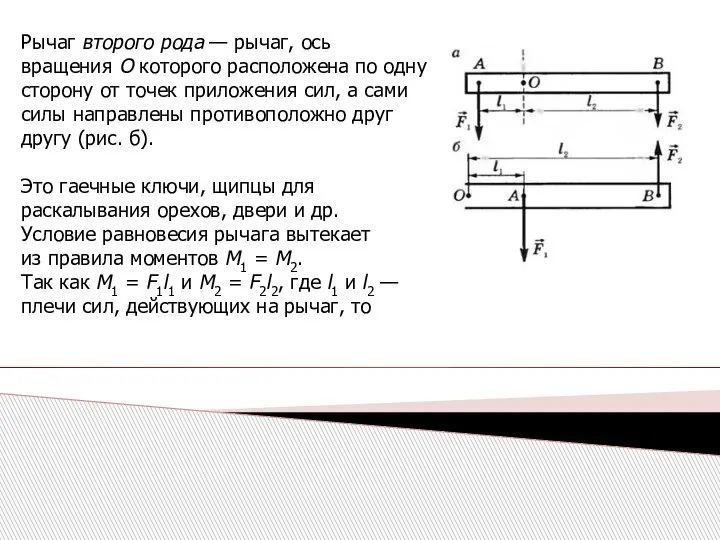
- 31. Рычаг второго рода — рычаг, ось вращения О которого расположена по одну сторону от точек приложения
- 32. условие равновесия рычага При равновесии рычага под действием двух сил модули этих сил обратно пропорциональны их
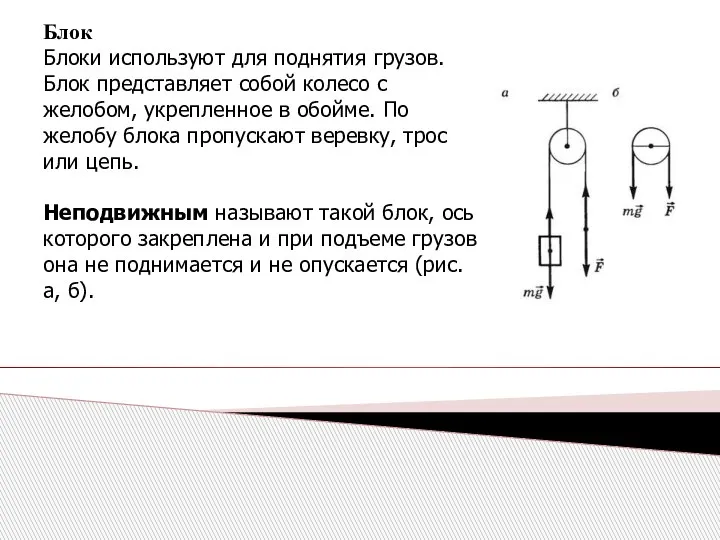
- 33. Блок Блоки используют для поднятия грузов. Блок представляет собой колесо с желобом, укрепленное в обойме. По
- 34. Неподвижный блок можно рассматривать как равноплечий рычаг, у которого плечи приложенных сил равны радиусу колеса Следовательно,
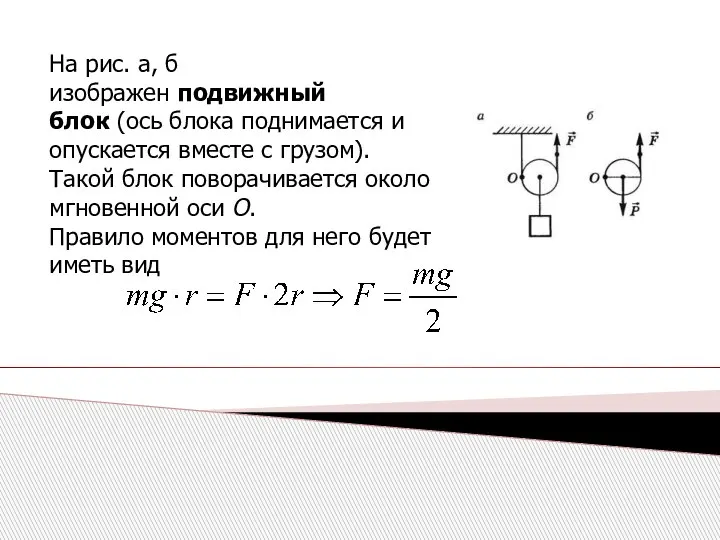
- 35. На рис. а, б изображен подвижный блок (ось блока поднимается и опускается вместе с грузом). Такой
- 36. Таким образом, подвижный блок дает выигрыш в силе в два раза. Обычно на практике применяют комбинацию
- 37. Равенство работ при использовании простых механизмов Мы видим, что с помощью простых механизмов можно получить выигрыш
- 38. Подставим найденные значения силы и получим Таким образом, работа AF равна работе, которую нужно совершить, чтобы
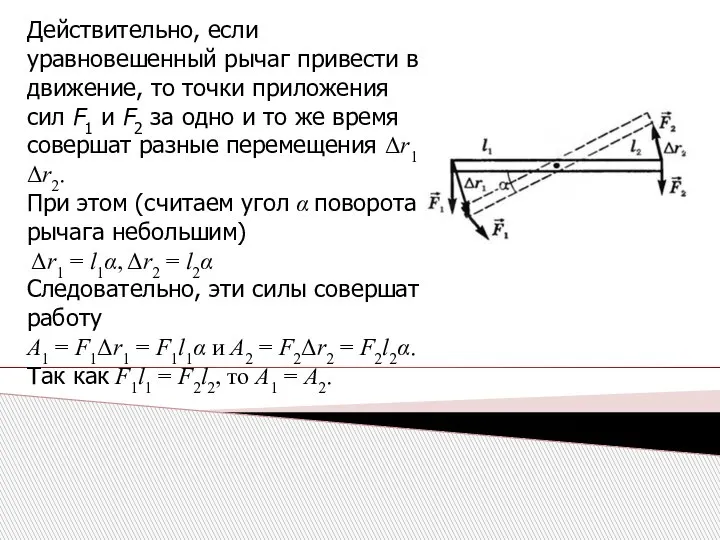
- 39. Действительно, если уравновешенный рычаг привести в движение, то точки приложения сил F1 и F2 за одно
- 40. При использовании неподвижного блока мы видим, что приложенные силы F и mg равны и пути, пройденные
- 41. Таким образом, получая выигрыш в силе в два раза, проигрывают в два раза в перемещении, следовательно,
- 42. При рассмотрении простых механизмов мы не учитываем трение, а также вес самих механизмов. В реальных условиях
- 43. Эффективность работы механизма характеризуют коэффициентом полезного действия (КПД механизма) Коэффициент полезного действия — физическая величина, равная
- 45. Скачать презентацию



























 2. Механические, конструкционные и эксплуатационные свойства материалов
2. Механические, конструкционные и эксплуатационные свойства материалов Магниты и их свойства. Магнетизм
Магниты и их свойства. Магнетизм Стационарный режим работы однопоточного теплообменного аппарата
Стационарный режим работы однопоточного теплообменного аппарата Интерференция света
Интерференция света Решение задач на силу Ампера и силу Лоренца. Урок 51
Решение задач на силу Ампера и силу Лоренца. Урок 51 Допуски, посадки и контроль шпоночных соединений деталей
Допуски, посадки и контроль шпоночных соединений деталей Уравнения материального баланса. Уравнение Бернулли, уравнение неразрывности
Уравнения материального баланса. Уравнение Бернулли, уравнение неразрывности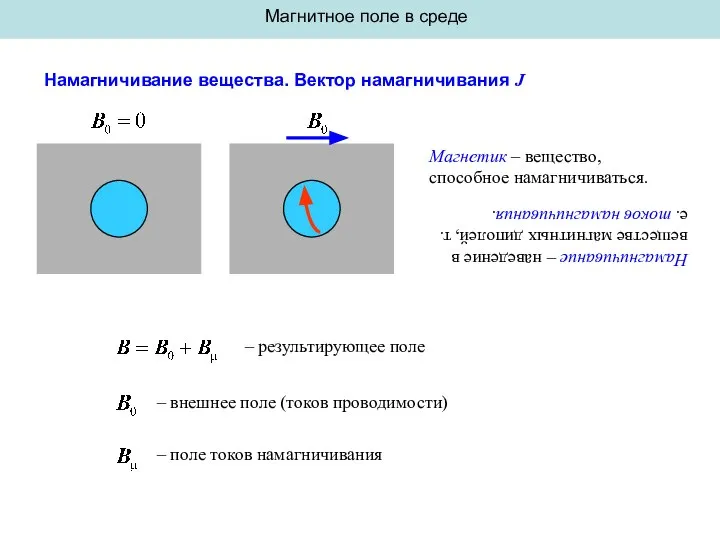 Намагничивание вещества. Вектор намагничивания J
Намагничивание вещества. Вектор намагничивания J Вычисление силы тяжести
Вычисление силы тяжести урок 1 - 11 клас
урок 1 - 11 клас Презентация на тему Построения в линзах
Презентация на тему Построения в линзах  Случайности не случайны! А вас бьет током? 4 класс
Случайности не случайны! А вас бьет током? 4 класс Механические колебания
Механические колебания Updated_Строение атома
Updated_Строение атома Электрические явления. Основные понятия
Электрические явления. Основные понятия Давление. Фонтан Герона
Давление. Фонтан Герона Основы термодинамики
Основы термодинамики Svobodnoe_padenie (1)
Svobodnoe_padenie (1) Задача: расчет процесса водяного пара
Задача: расчет процесса водяного пара Термодинамика высокоэластичной деформации
Термодинамика высокоэластичной деформации Элионные технологии. Расчет режимов элионной обработки и показателей качества изделий
Элионные технологии. Расчет режимов элионной обработки и показателей качества изделий Физические величины. Измерение физических величин. Точность и погрешность измерений
Физические величины. Измерение физических величин. Точность и погрешность измерений Паровая машина Ползунова
Паровая машина Ползунова Винт Архимеда
Винт Архимеда Как уменьшить силу трения
Как уменьшить силу трения Соединения проводников. Задачи
Соединения проводников. Задачи Принципы проектирования машин
Принципы проектирования машин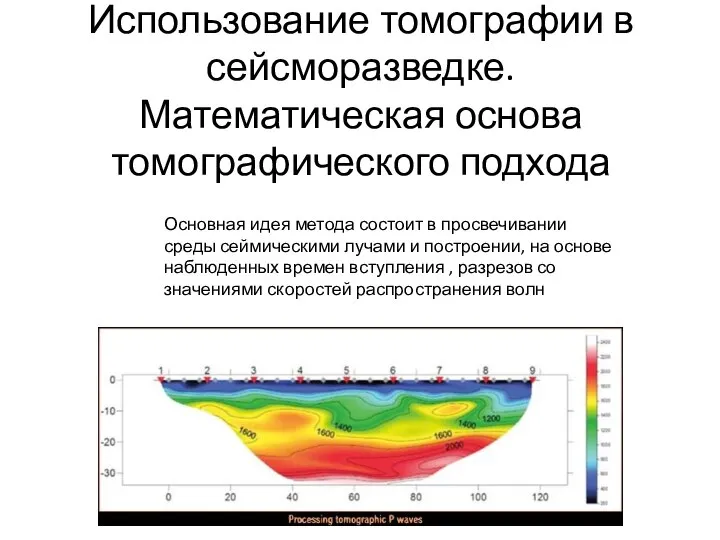 Использование томографии в сейсморазведке. Математическая основа томографического подхода
Использование томографии в сейсморазведке. Математическая основа томографического подхода