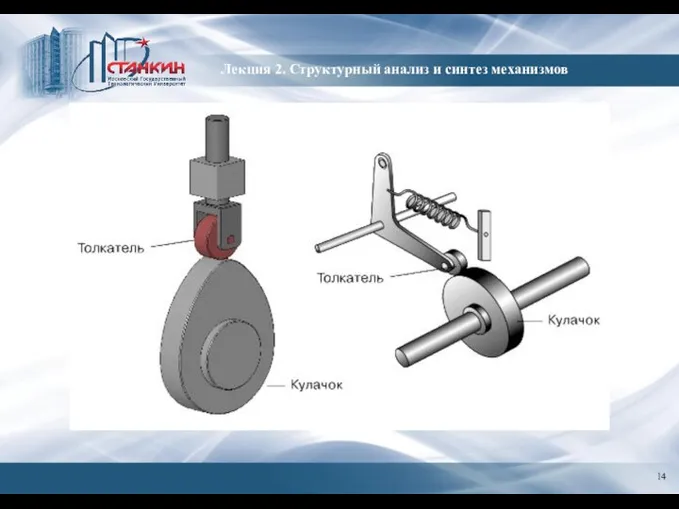
Структурный анализ и синтез механизмов. Лекция 2

Лекция 2. Структурный анализ и синтез механизмов
Степень свободы – это возможность простейшего движения твердого тела.
Рис. 2.1. Степени свободы в пространстве
ВВВППП
В – вращательное движение
П – поступательное движение
В пространстве 6 степеней свободы: ЧСС = 6
2

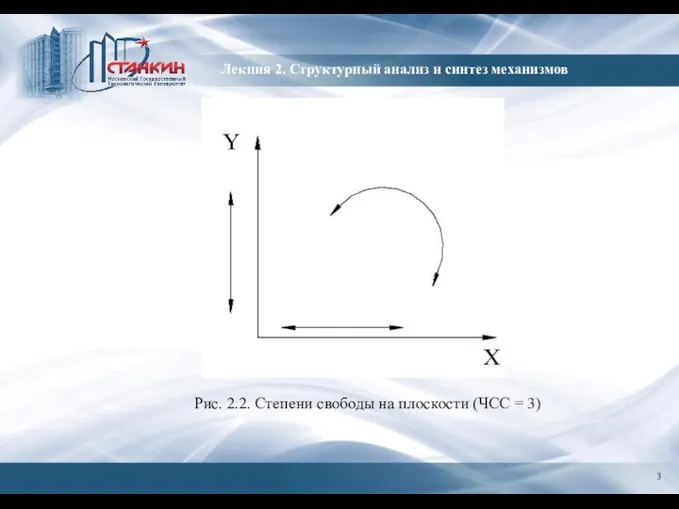
Лекция 2. Структурный анализ и синтез механизмов
Рис. 2.2. Степени свободы на плоскости (ЧСС = 3)
3

Лекция 2. Структурный анализ и синтез механизмов
Кинематические пары накладывают ограничение на возможные относительные движения тела. Ограничения, накладываемые кинематической парой на относительное движение звена или тела, называется связью.
Число степеней свободы (ЧСС).
Число условий связи (ЧУС): Если ЧУС≤3 – механизм рассматривается в плоскости.
Если 3<ЧУС≤6 – механизм рассматривается в пространстве.
Для пространства: ЧУС + ЧСС = 6.
Для плоскости: ЧУС + ЧСС = 3.
Рис. 2.3 Пример механизма с одной степенью свободы
4

Лекция 2. Структурный анализ и синтез механизмов
Кинематические пары классифицируются по подвижностям - классификация Добровольского (по родам) (основная) или по классам (классификация Артоболевского).
Подвижность или род кинематической пары определяется через число степеней свободы. Для определения ЧСС необходимо одно из звеньев кинематической пары условно сделать неподвижным, посмотреть какие движения совершает другое звено, и подсчитать их.
5

Лекция 2. Структурный анализ и синтез механизмов
Пятиподвижная кинематическая пара (5П) – кинематическая пара 1-го класса, допускает пять относительных движений при одном условии связи. На рис. 2.4 представлена пара шар-плоскость. Это высшая кинематическая пара, т.к. ее элементы соприкасаются в точке.
Рис. 2.4. Пример пятиподвижной кинематической пары
P5 – пятиподвижная КП;
PI – КП 1-го класса.
6

Лекция 2. Структурный анализ и синтез механизмов
Четырехподвижная кинематическая пара (4П) – кинематическая пара 2-го класса, допускает лишь четыре относительных движения при двух условиях связи. На рис. 2.5 представлен пара цилиндр-плоскость. Она является высшей кинематической парой, т.к. ее элементы соприкасаются по линиям. Пара цилиндр-плоскость требует силового замыкания.
Рис. 2.5. Пример четырехподвижной кинематической пары
P4 –четырехподвижная КП;
PII – КП 2-го класса.
7

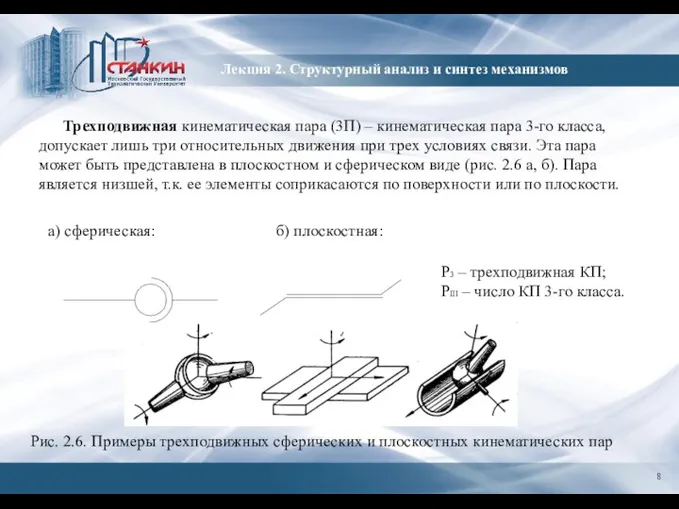
Лекция 2. Структурный анализ и синтез механизмов
Трехподвижная кинематическая пара (3П) – кинематическая пара 3-го класса, допускает лишь три относительных движения при трех условиях связи. Эта пара может быть представлена в плоскостном и сферическом виде (рис. 2.6 а, б). Пара является низшей, т.к. ее элементы соприкасаются по поверхности или по плоскости.
P3 – трехподвижная КП;
PIII – число КП 3-го класса.
а) сферическая:
б) плоскостная:
Рис. 2.6. Примеры трехподвижных сферических и плоскостных кинематических пар
8

Лекция 2. Структурный анализ и синтез механизмов
Двухподвижная кинематическая пара (2П) – кинематическая пара 4-го класса, допускает два относительных движения при четырех условиях связи. Эта пара может быть представлена в цилиндрическом и сферическом с пальцем видах (рис. 2.7). Это низшая кинематическая пара, т.к. ее элементы соприкасаются по поверхностям.
P2 – двухподвижная КП;
PIV – число КП 4-го класса.
а) цилиндрическая:
б) сферическая кинематическая пара с пальцем:
Рис. 2.7. Примеры двухподвижных цилиндрических и сферических кинематических пар
9

Одноподвижная кинематическая пара (1П) – кинематическая пара 5-го класса, допускает только лишь одно относительное движение при пяти условиях связи. Эта пара может быть представлена во вращательном или поступательном видах. К одноподвижным кинематическим парам относят винтовую пару, в которой винтовое движение является зависимым от вращательного и поступательного относительных движений, т.е. одно движение не может быть осуществлено без другого. Элементы одноподвижной кинематической пары соприкасаются либо по поверхности, либо по плоскости, т.е. она является низшей кинематической парой (рис. 2.8).
а) вращательная кинематическая пара:
б) поступательная кинематическая пара:
в) винтовая кинематическая пара:
P1 – одноподвижная КП;
PV – число КП 5-го класса.
Лекция 2. Структурный анализ и синтез механизмов
10

Лекция 2. Структурный анализ и синтез механизмов
10

Число степеней свободы механизмов характеризует число двигателей необходимых для нормальной работы механизмов.
Число степеней свободы механизмов (W) – это число вариаций обобщенных координат механизма (число простейших движущихся и ведущих звеньев механизма).
Обобщенная координата – независимая координата, однозначно определяющая положение всех звеньев механизма относительно стойки.
φ – обобщенная координата (рис. 2.9).
Рис. 2.9. Пример кривошипно-ползунного механизма и определения его обобщенной координаты
Лекция 2. Структурный анализ и синтез механизмов
11

Лекция 2. Структурный анализ и синтез механизмов
Для определения ЧСС (W) механизма необходимо сосчитать все подвижности звеньев механизмов и отбросить связи, накладываемые кинематическими парами. Для плоского механизма:
«3» – ЧСС одного звена;
«n» – число звеньев механизма;
«n-1» – число подвижных звеньев механизма;
«3(n-1)» – число степеней свободы подвижных звеньев механизма;
«P1» –число одноподвижных КП;
«2» – число связей, накладываемое одной одноподвижной КП;
«2P1»– число связей, накладываемых всеми одноподвижными КП;
«P2»– число двуподвижных КП;
«1» – число связей, накладываемых одной двуподвижной КП;
«1P2»– число связей, накладываемых всеми двуподвижными КП;
Тогда,
– формула Чебышева.
, т.к. контакт в точке;
12

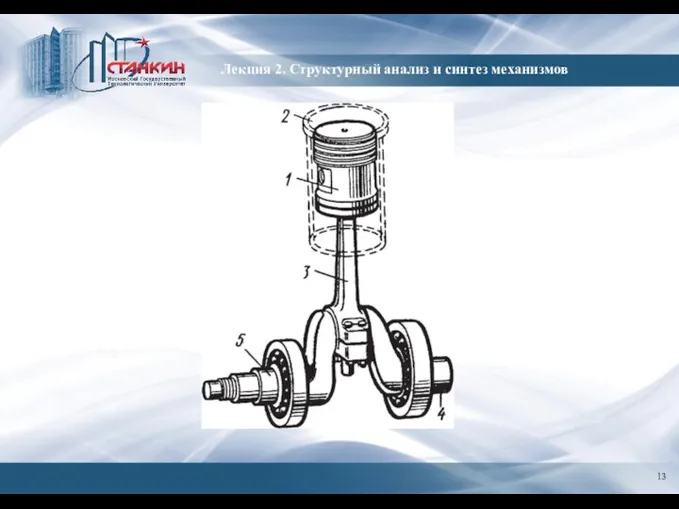
Пример 2.1. Пример механизма с числом вариаций обобщенных координат равным одному (рис. 2.10):
Рис. 2.10. Пример кривошипно-ползунного механизма
n = 4;
P1 = 4;
P2 = 0;
Лекция 2. Структурный анализ и синтез механизмов
13

Лекция 2. Структурный анализ и синтез механизмов
13

Лекция 2. Структурный анализ и синтез механизмов
Пример 2.2. Пример механизма с числом вариаций обобщенных координат равным двум (рис. 2.11):
Рис. 2.11. Пример кулачкового механизма
n = 4;
P1 = 3;
P2 = 1;
14

Лекция 2. Структурный анализ и синтез механизмов
14

Лекция 2. Структурный анализ и синтез механизмов
По аналогии для пространственного механизма, получили формулу для определения числа степеней свободы (формула Малышева):
15

Лекция 2. Структурный анализ и синтез механизмов
Пример 2.3. Пример механизма с числом вариаций обобщенных координат равным семи (рис. 2.12):
Рис. 2.12. Пример манипуляционного механизма
n = 4;
P1 = 1;
P2 = 0;
P3 = 2;
P4 = 0;
P5 = 0.
16

Лекция 2. Структурный анализ и синтез механизмов
Метрическая связь - связь, повторяющая действия других связей механизма. Она возникает в механизме при добавлении к нему звена с двумя одноподвижными КП. Связь вводится в механизм с целью повышения его жесткости или обеспечения определенности движении его звеньев.
На рис. 2.13 представлен механизм с метрической связью.
Рис. 2.13. Механизм с метрической связью
n = 5;
P1 = 6;
P2 = 0.
Определить W (число степеней свободы):
17

Лекция 2. Структурный анализ и синтез механизмов
Этот механизм с нулевой подвижностью (ферма). Звено 4 с КП в точках Е и В является метрической связью, не нарушая работу механизма, она повышает его жесткость. При исследовании метрические связи отбрасывают.
Число метрических связей (qм) в механизме определяют по формуле:
где
WФ – фактическое число степеней свободы механизма (число подвижных звеньев, движение которых задано).
В примере (рис. 2.13): WФ = 1, W = 0;
– одна метрическая связь.
18