Содержание
- 2. Применение функций комплексного переменного для описания плоскопараллельных полей
- 3. Линии равного потенциала в плоскости xOy определяются уравнением: - поток вектора сквозь поверхность, которую описал бы
- 4. Выражение для напряженности через функцию потока Для декартовой системы координат: Условимся считать функцию потока, возрастающей влево
- 5. Уравнения Лапласа для функций потенциала и потока Продифференцируем первое уравнение по x , а второе по
- 6. Функция комплексного переменного z = x+jy = r·e jθ Плоскость комплексного переменного Рассмотрим комплексную величину: -
- 7. Сравнение условий Коши-Римана и выражений для напряженности поля: - комплексный потенциал поля Составляющие напряженности поля :
- 8. (1) Подставляя (2) в (1) , получаем: (2) Задача расчета поля решена, если найдена аналитическая функция
- 9. Метод заданного комплексного потенциала. Этот метод расчета плоскопараллельных полей заключается в предварительном задании некоторой комплексной функции
- 10. При а > 0 с ростом x и y растут соответственно V и U . Принимая
- 11. ΙΙ. Пусть комплексный потенциал задан в виде: W(z) = jA ln z = jA ln(r·ejθ) =
- 12. Поле уединенного заряженного кругового цилиндра При θ =2π получаем поверхность, охватывающую весь проводник с полным зарядом
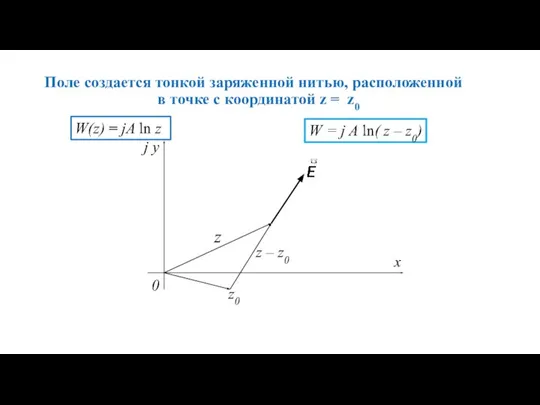
- 13. Поле создается тонкой заряженной нитью, расположенной в точке с координатой z = z0 W = j
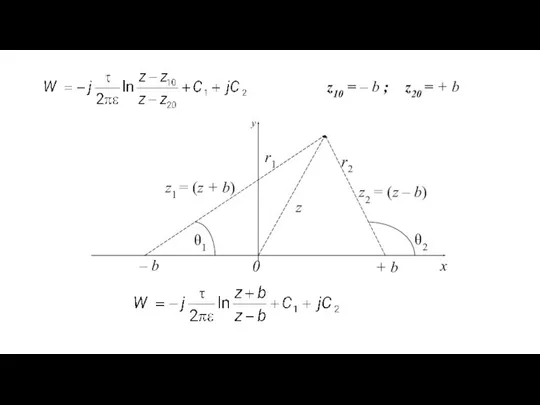
- 14. ΙΙΙ. Поле двух тонких заряженных нитей Для двух заряженных нитей с зарядами τ1 и τ2, расположенных
- 15. z10 = – b ; z20 = + b + b – b 0 θ1 θ2
- 16. z1 = z + b = r1 z2 = z – b = r2 = V
- 17. Линии равного потенциала – это окружности с центрами на оси OX с координатами центра: и радиусом:
- 18. Линии равной напряженности поля в системе двух заряженных проводов Положив в выражении для функции потока C1=0,
- 19. Картина поля двух линейных проводов и реальной линии передачи Формулы для определения положения линейных проводов (электрических
- 21. Скачать презентацию
















 Что изучает физика? (7 класс)
Что изучает физика? (7 класс) Оптика. Раздел 5
Оптика. Раздел 5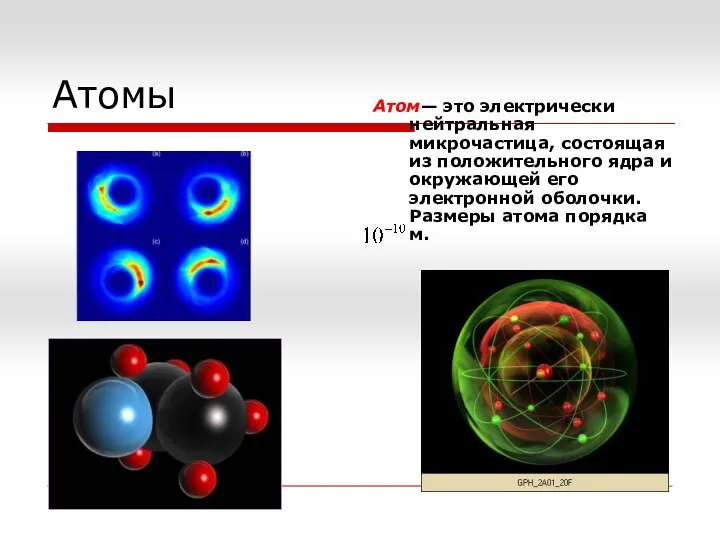 Атомы
Атомы Термометр Галілея
Термометр Галілея Теория суперструн
Теория суперструн Топливо будущего
Топливо будущего Квантовая механика
Квантовая механика Устройство и ремонт унифицированной гидропередачи УГП-1200
Устройство и ремонт унифицированной гидропередачи УГП-1200 Силы, действующие на поезд. Теория электрической тяги
Силы, действующие на поезд. Теория электрической тяги 7 кл Три состояния вещ-ва
7 кл Три состояния вещ-ва Нанотехнологии и их применение
Нанотехнологии и их применение Последовательное и параллельное соединение проводников
Последовательное и параллельное соединение проводников Магнитное взаимодействие Изучение свойств магнита Учитель И.А. Попова
Магнитное взаимодействие Изучение свойств магнита Учитель И.А. Попова Тепловые балансы. Основное уравнение теплопередачи
Тепловые балансы. Основное уравнение теплопередачи Дисперсия света. Интерференция механических волн
Дисперсия света. Интерференция механических волн Знаменитые физики 20 века и их заслуги
Знаменитые физики 20 века и их заслуги Активация в ядерной физике. (Тема 2.8)
Активация в ядерной физике. (Тема 2.8) Концепции современного естествознания
Концепции современного естествознания Принцип относительности Галилея. Инвариантные и относительные физические величины
Принцип относительности Галилея. Инвариантные и относительные физические величины Напряжение в точке включения реактора. Распределение напряжения по линии. Задача
Напряжение в точке включения реактора. Распределение напряжения по линии. Задача Приводные муфты
Приводные муфты Теплофизика процесса резания
Теплофизика процесса резания Инерция. Г. Галилей
Инерция. Г. Галилей Презентация на тему Прямолинейное равномерное движение
Презентация на тему Прямолинейное равномерное движение  Нерезьбовые соединения. Шпоночное соединение
Нерезьбовые соединения. Шпоночное соединение Импульс тела. Решение задач
Импульс тела. Решение задач Интеллектуальная игра. Машины
Интеллектуальная игра. Машины Фундаментальные и прикладные задачи гидромеханики
Фундаментальные и прикладные задачи гидромеханики