Содержание
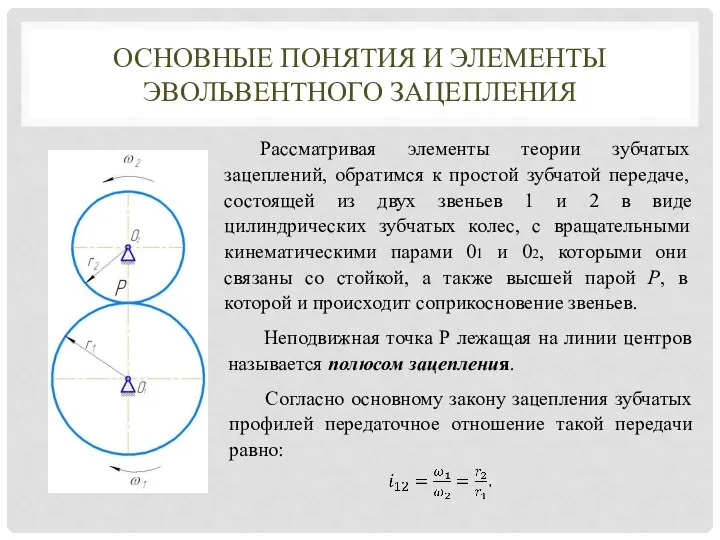
- 2. Рассматривая элементы теории зубчатых зацеплений, обратимся к простой зубчатой передаче, состоящей из двух звеньев 1 и
- 3. ОСНОВНЫЕ ПОНЯТИЯ И ЭЛЕМЕНТЫ ЭВОЛЬВЕНТНОГО ЗАЦЕПЛЕНИЯ (ПРОДОЛЖЕНИЕ)
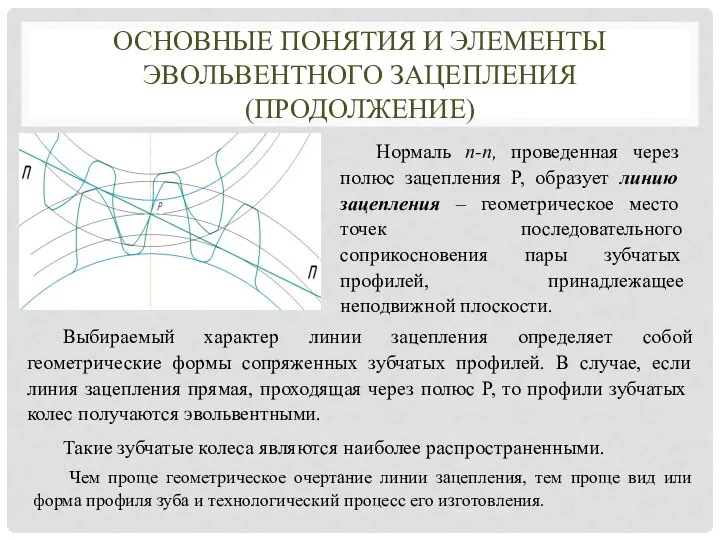
- 4. Нормаль n-n, проведенная через полюс зацепления Р, образует линию зацепления – геометрическое место точек последовательного соприкосновения
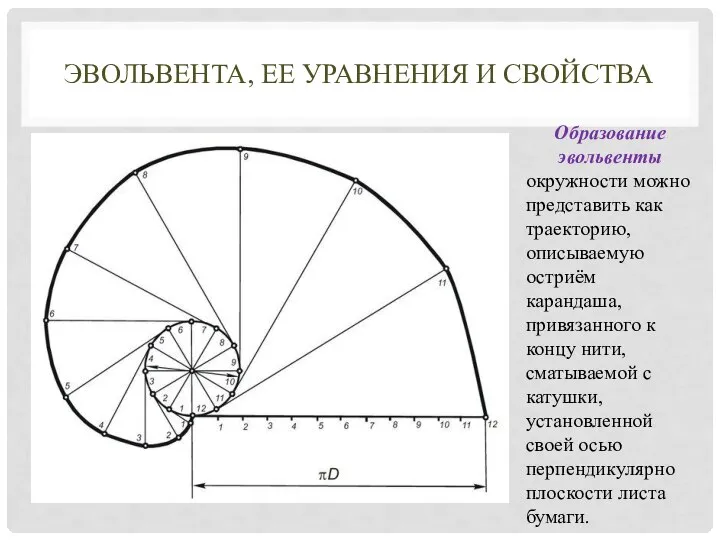
- 5. ЭВОЛЬВЕНТА, ЕЕ УРАВНЕНИЯ И СВОЙСТВА Образование эвольвенты окружности можно представить как траекторию, описываемую остриём карандаша, привязанного
- 6. ЭВОЛЬВЕНТА, ЕЕ УРАВНЕНИЯ И СВОЙСТВА Тогда эвольвента окружности представляет собой траекторию любой точки прямой, перекатываемой без
- 7. ЭВОЛЬВЕНТА, ЕЕ УРАВНЕНИЯ И СВОЙСТВА (ПРОДОЛЖЕНИЕ) Свойства эвольвенты: 1. Нормаль к эвольвенте касается основной окружности; точка
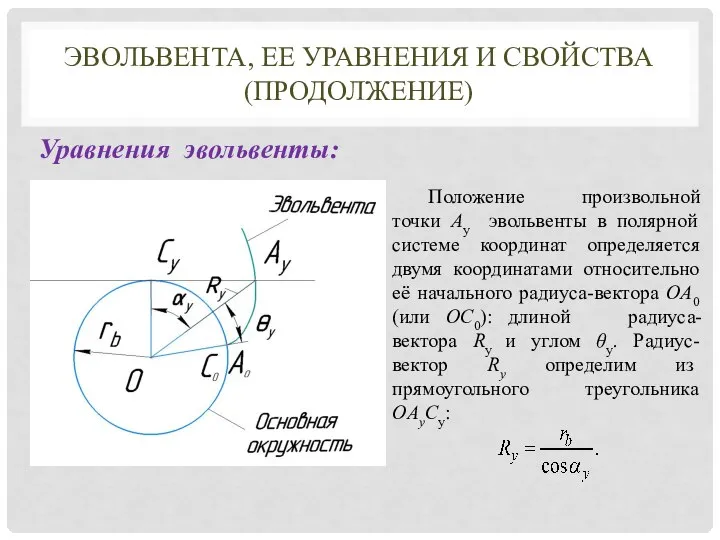
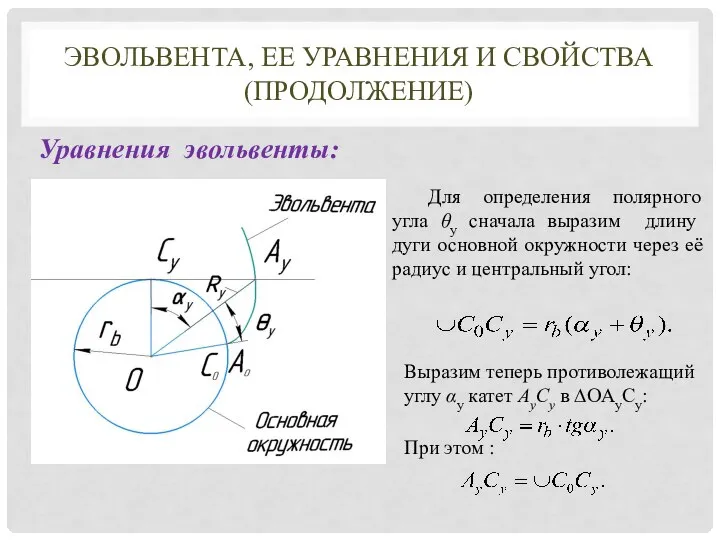
- 8. ЭВОЛЬВЕНТА, ЕЕ УРАВНЕНИЯ И СВОЙСТВА (ПРОДОЛЖЕНИЕ) Уравнения эвольвенты: Положение произвольной точки Ay эвольвенты в полярной системе
- 9. ЭВОЛЬВЕНТА, ЕЕ УРАВНЕНИЯ И СВОЙСТВА (ПРОДОЛЖЕНИЕ) Уравнения эвольвенты: Для определения полярного угла θy сначала выразим длину
- 10. ЭВОЛЬВЕНТА, ЕЕ УРАВНЕНИЯ И СВОЙСТВА (ПРОДОЛЖЕНИЕ) Уравнения эвольвенты: Подставляя в это равенство соответствующие выражения и решая
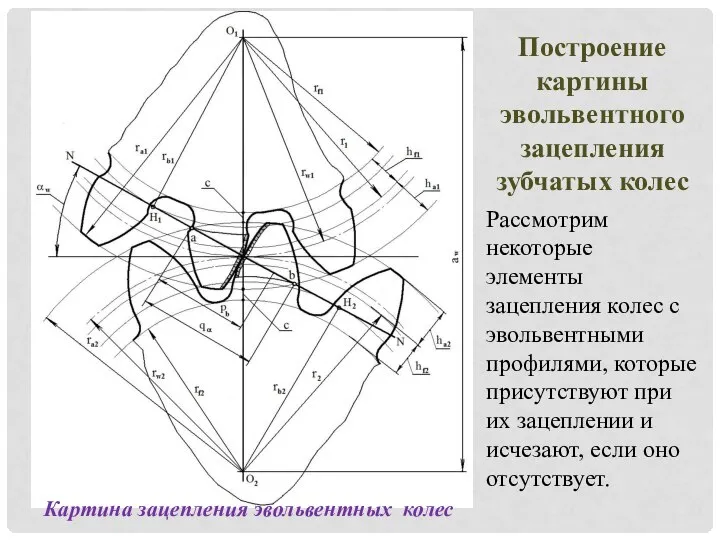
- 11. Картина зацепления эвольвентных колес Рассмотрим некоторые элементы зацепления колес с эвольвентными профилями, которые присутствуют при их
- 12. КАРТИНА ЗАЦЕПЛЕНИЯ ЭВОЛЬВЕНТНЫХ КОЛЕС (ПРОДОЛЖЕНИЕ) К ним относятся: 1. Межосевое расстояние аw - это кратчайшее расстояние
- 13. 6. Угол αw между нормалью к контактирующим поверхностям зубьев и общей касательной к начальным поверхностям (окружностям)
- 14. МЕТОДЫ НАРЕЗАНИЯ ЗУБЧАТЫХ КОЛЕС В зависимости от способа формообразования различают два метода нарезания зубчатых колес: метод
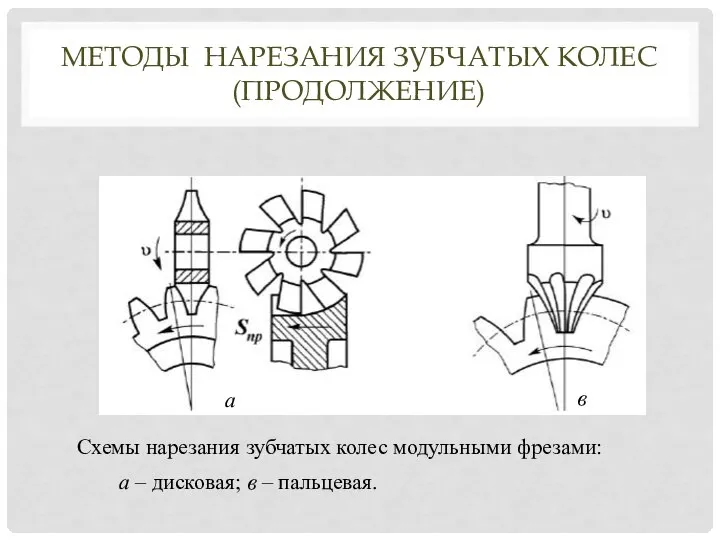
- 15. МЕТОДЫ НАРЕЗАНИЯ ЗУБЧАТЫХ КОЛЕС (ПРОДОЛЖЕНИЕ) Схемы нарезания зубчатых колес модульными фрезами: а – дисковая; в –
- 16. Для изготовления колес высокой точности используется метод обката. Профиль зуба колеса, нарезаемого по методу обката, формируется
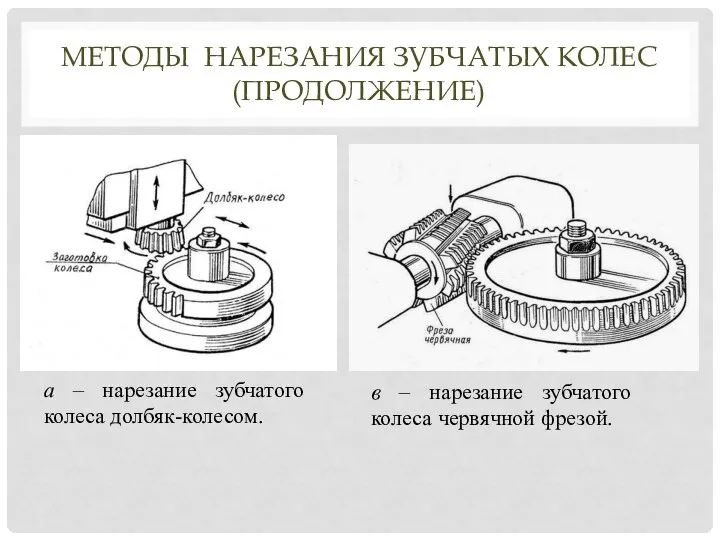
- 17. а – нарезание зубчатого колеса долбяк-колесом. в – нарезание зубчатого колеса червячной фрезой. МЕТОДЫ НАРЕЗАНИЯ ЗУБЧАТЫХ
- 18. ТЕОРЕТИЧЕСКИЙ ИСХОДНЫЙ И ИСХОДНЫЙ ПРОИЗВОДЯЩИЙ КОНТУРЫ Форма главной поверхности зуба колеса определяется геометрией режущей кромки инструмента.
- 19. ТЕОРЕТИЧЕСКИЙ ИСХОДНЫЙ И ИСХОДНЫЙ ПРОИЗВОДЯЩИЙ КОНТУРЫ Основные параметры теоретического исходного контура : Угол главного профиля α.
- 20. ТЕОРЕТИЧЕСКИЙ ИСХОДНЫЙ И ИСХОДНЫЙ ПРОИЗВОДЯЩИЙ КОНТУРЫ В соответствии со стандартом основные размеры теоретического исходного контура определяются
- 22. Скачать презентацию











 Основы гидравлики
Основы гидравлики Сверлильный станок
Сверлильный станок Производная в физике и технике
Производная в физике и технике Обработка спектров
Обработка спектров svobodnoe_padenie_tel_kopiya
svobodnoe_padenie_tel_kopiya Закон Ома. Светодиоды. Кнопки
Закон Ома. Светодиоды. Кнопки Метод узлового напряжения
Метод узлового напряжения Источники электрической энергии. Системы электроснабжения воздушных судов. Тема 6
Источники электрической энергии. Системы электроснабжения воздушных судов. Тема 6 Последовательное соединение
Последовательное соединение Составные части велосипеда
Составные части велосипеда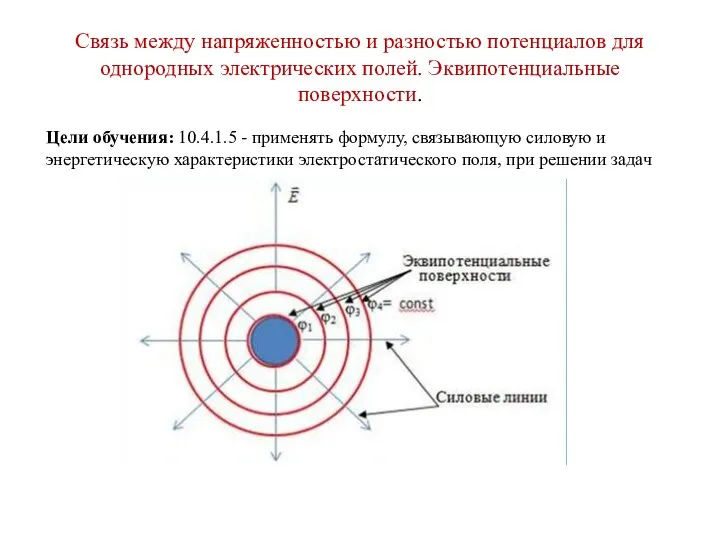 Эквипотенциальные поверхности
Эквипотенциальные поверхности Электростатика. Цели и задачи
Электростатика. Цели и задачи Robust Control of Quantum Systems: Limitations or No Fundamental Limitations?
Robust Control of Quantum Systems: Limitations or No Fundamental Limitations? 2_Волны
2_Волны Алюминий и его сплавы, их характеристика. Деформируемые и литейные сплавы алюминия. Порошковые сплавы. (Лекция 13)
Алюминий и его сплавы, их характеристика. Деформируемые и литейные сплавы алюминия. Порошковые сплавы. (Лекция 13) Статика. Устойчивое равновесие тел
Статика. Устойчивое равновесие тел Презентация_Кинематика криволинейное движение (2)
Презентация_Кинематика криволинейное движение (2) Полезные свойства кавитации
Полезные свойства кавитации Французский язык
Французский язык Презентация на тему Механическая работа и мощность
Презентация на тему Механическая работа и мощность  Физика плазмы
Физика плазмы Строение атома
Строение атома History. Классикалық механиканың негізгін қалаған ғалым
History. Классикалық механиканың негізгін қалаған ғалым Применение скакалки, каната на занятиях физической культуры и внеурочной деятельности
Применение скакалки, каната на занятиях физической культуры и внеурочной деятельности Пузырьковая камера
Пузырьковая камера DZ-3
DZ-3 Презентация по физике "Парогенераторы АЭС" -
Презентация по физике "Парогенераторы АЭС" -  Измерение давления
Измерение давления