Содержание
- 2. План темы Тепловые состояния Условия применимости модели Макроскопическое тело Термостат Макро- и микроскопическое описание теплового состояния
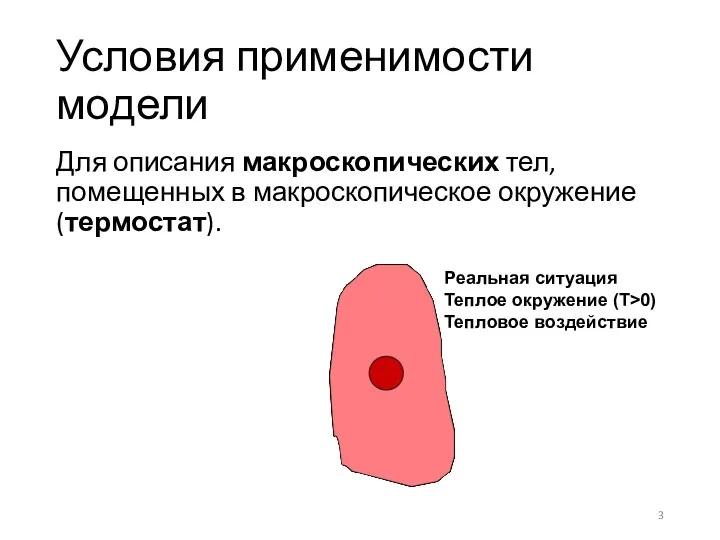
- 3. Условия применимости модели Для описания макроскопических тел, помещенных в макроскопическое окружение (термостат). Реальная ситуация Теплое окружение
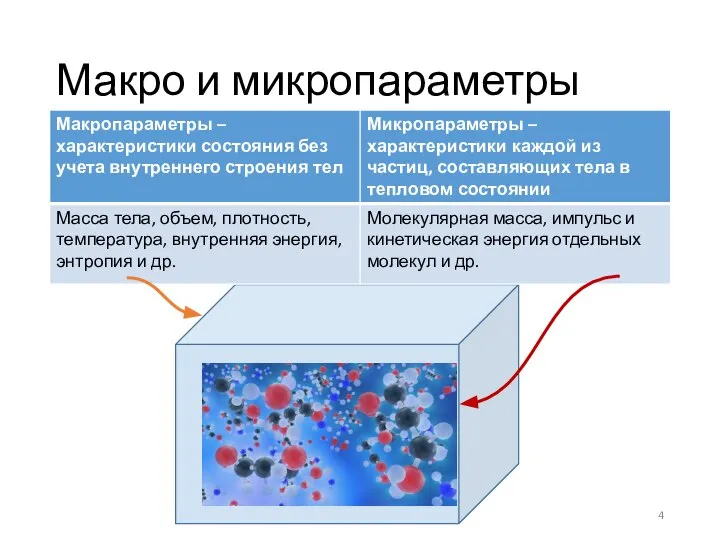
- 4. Макро и микропараметры
- 5. Тепловое равновесие (Т.Р.) – фундаментальная модель Только состоянию Т.Р. можно приписать определённую температуру. В состоянии Т.Р.
- 6. Температура (Т) Макроскопический параметр состояния: Метка теплового равновесия Операциональное определение: То, что измеряют термометром А чем
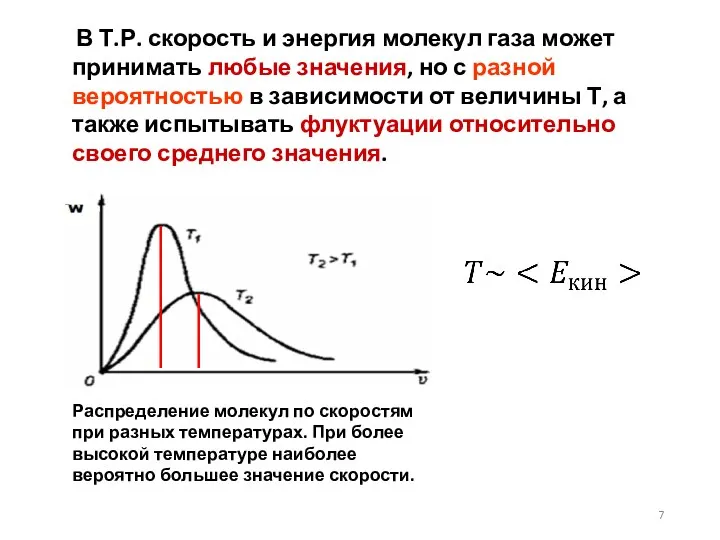
- 7. В Т.Р. скорость и энергия молекул газа может принимать любые значения, но с разной вероятностью в
- 8. Лорд Кельвин (Уильям Томсон) - создатель создатель абсолютной шкалы - 1848г. (1824-1907)
- 9. Термометр Термометрическое тело должно однозначно реагировать на изменение температуры; Термометрические жидкости: ртуть, спирт, вода и т.д.
- 10. Итак, температура Это метка состояния теплового равновесия, которая, будучи неаддитивной величиной имеет адекватное выражение лишь с
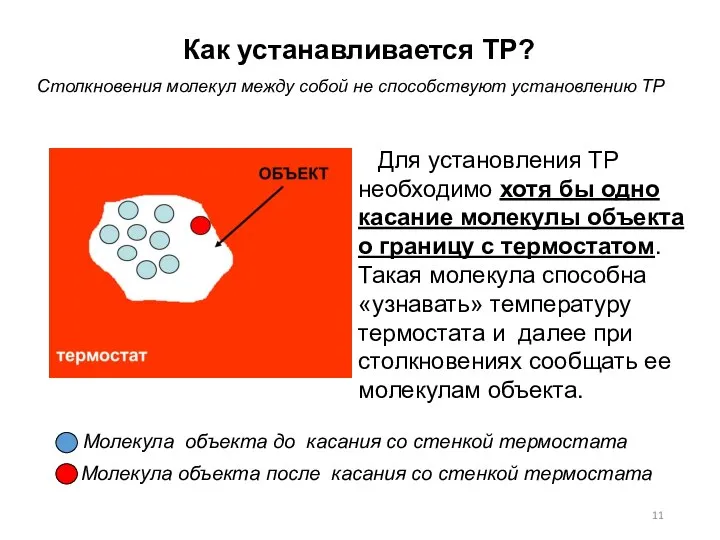
- 11. Для установления ТР необходимо хотя бы одно касание молекулы объекта о границу с термостатом. Такая молекула
- 12. При всяком контакте с окружением Объект может получать от него или отдавать ему определённую энергию. В
- 13. Внутренняя энергия (U) Макроскопическое описание: Чтобы перевести тело из одного агрегатного состояния в другое при данной
- 14. Баланс энергии для нециклических тепловых процессов (дебет = кредиту) Это первый закон (начало) термодинамики- науки о
- 15. «Неконвертируемость» теплоты и работы Теплота Q и работа A - два различных способа обмена энергией между
- 16. Совершая работу по сжатию газа, его можно таким образом нагреть, При этом можно добиться того, что
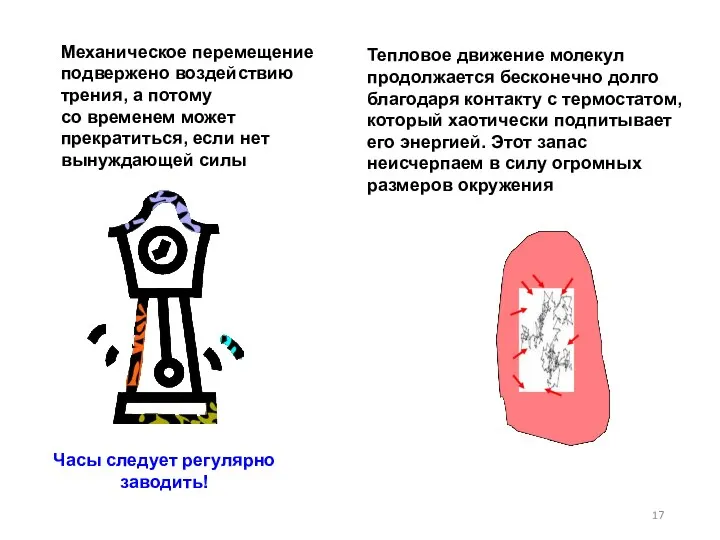
- 17. Механическое перемещение подвержено воздействию трения, а потому со временем может прекратиться, если нет вынуждающей силы Часы
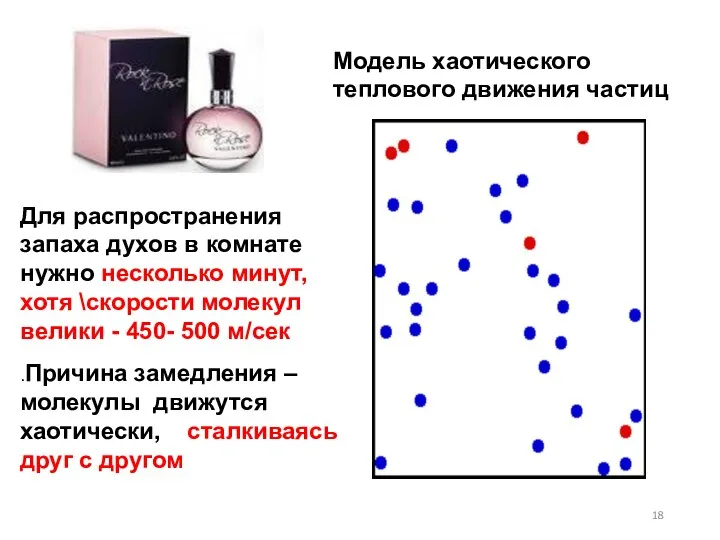
- 18. .Причина замедления – молекулы движутся хаотически, сталкиваясь друг с другом Для распространения запаха духов в комнате
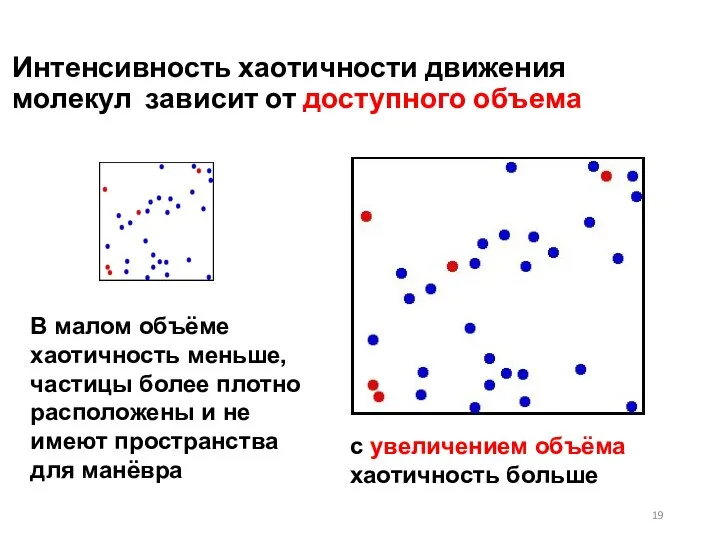
- 19. Интенсивность хаотичности движения молекул зависит от доступного объема В малом объёме хаотичность меньше, частицы более плотно
- 20. Скорость хаотического движения возрастает с повышением температуры Температура ниже Температура выше
- 21. Беспорядок и вероятность Порядок осуществляется одним единственным способом из множества возможных комбинаций. Вероятность обнаружить беспорядок значительно
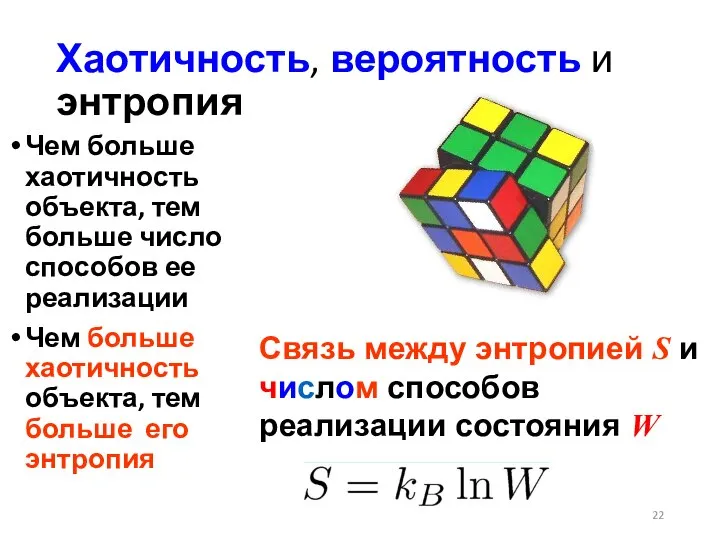
- 22. Хаотичность, вероятность и энтропия Чем больше хаотичность объекта, тем больше число способов ее реализации Чем больше
- 23. Л. Больцман S= k log W 1844-1906
- 24. Константа kB= 1,38 ∙10 -23 Дж/K названа именем Людвига Больцмана, который дал миру формулу, начертанную на
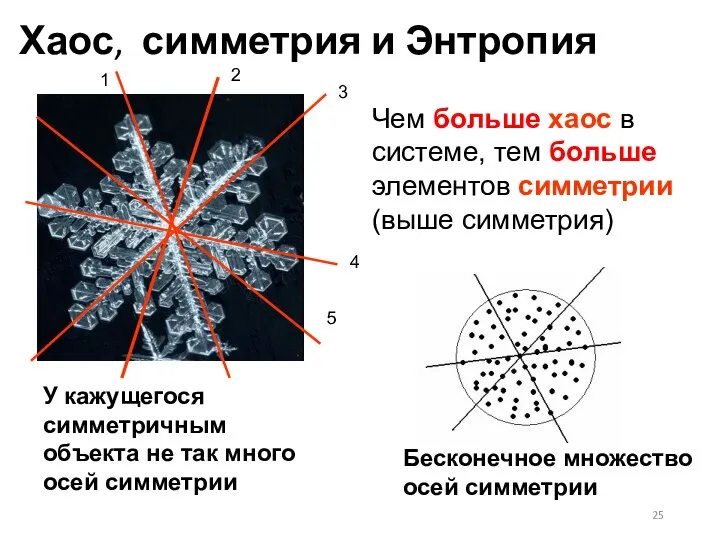
- 25. Хаос, симметрия и Энтропия Чем больше хаос в системе, тем больше элементов симметрии (выше симметрия) Бесконечное
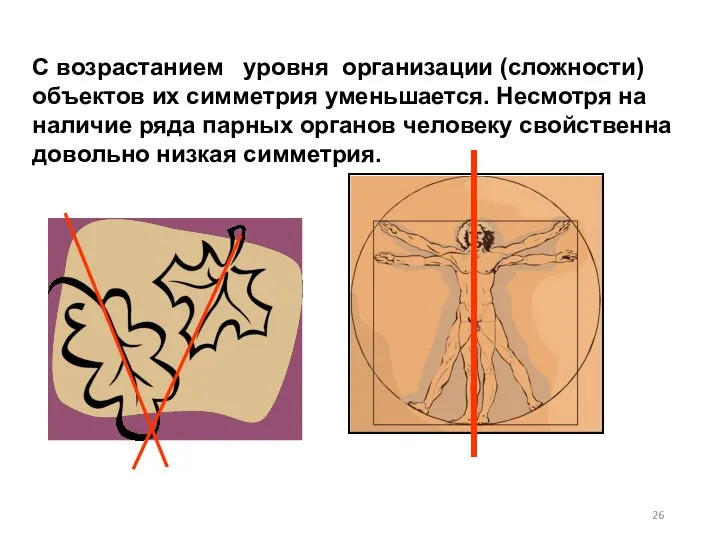
- 26. С возрастанием уровня организации (сложности) объектов их симметрия уменьшается. Несмотря на наличие ряда парных органов человеку
- 27. Квантовые состояния Лекция 5
- 28. План темы Квантовые состояния Условия применимости модели Микроскопическое тело, Квантовое окружение, Квантон Особые свойства квантонов Квантово-волновой
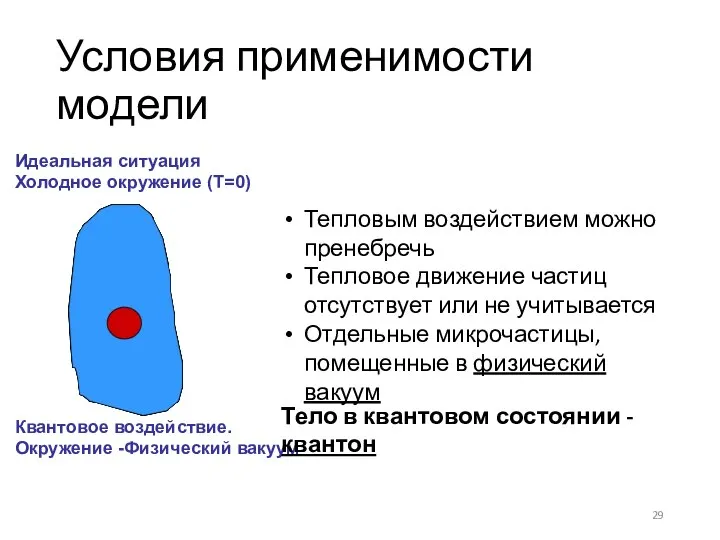
- 29. Условия применимости модели Идеальная ситуация Холодное окружение (Т=0) Квантовое воздействие. Окружение -Физический вакуум Тепловым воздействием можно
- 30. В неклассической ЕНКМ исходят из того, что под влиянием стохастического воздействия все характеристики объекта являются случайными.
- 31. Физический вакуум В отсутствие молекул пространство заполнено физическими полями из которых потенциально могли бы родиться частицы.
- 32. Они обнаруживают очень «необычное» поведение Быть может, эти электроны – Миры, где пять материков, Искусства, знанья,
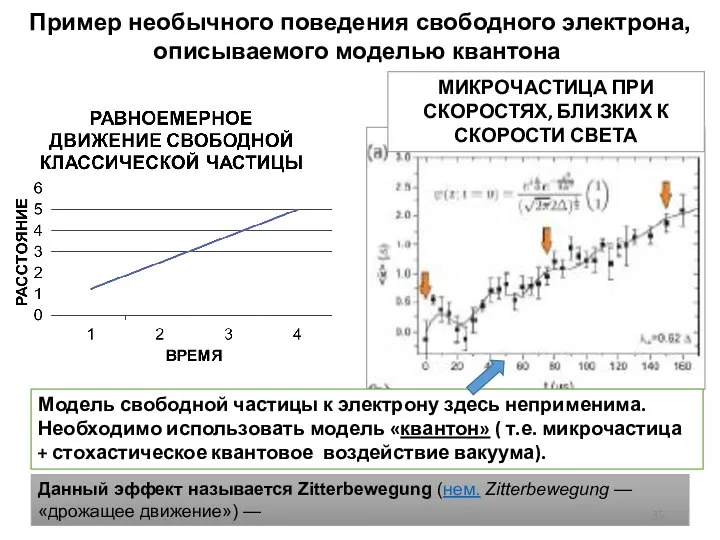
- 33. Пример необычного поведения свободного электрона, описываемого моделью квантона Свободная электрон в классическом подходе должен двигаться равномерно
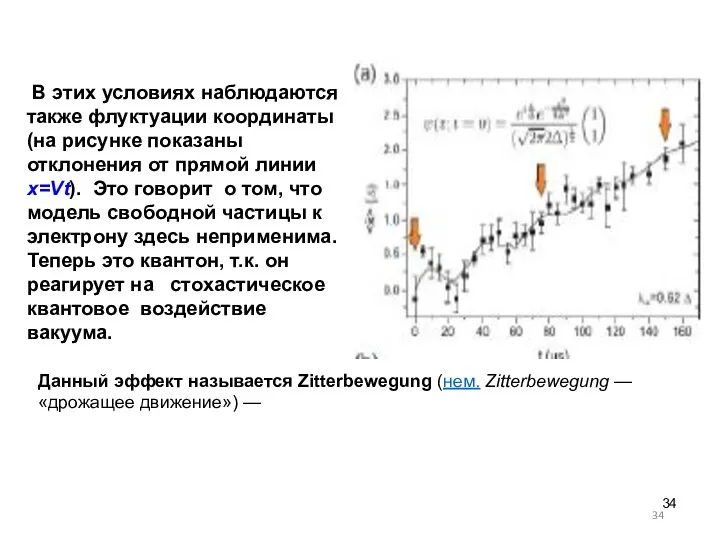
- 34. В этих условиях наблюдаются также флуктуации координаты (на рисунке показаны отклонения от прямой линии x=Vt). Это
- 35. Пример необычного поведения свободного электрона, описываемого моделью квантона Модель свободной частицы к электрону здесь неприменима. Необходимо
- 36. Квантово-волновой дуализм Макс Планк (1858-1947)
- 37. Квантово-волновой дуализм Луи де Бройль (1892-1987), Нобелевский лауреат 1929г. Франция Это соотношение указывает на связь между
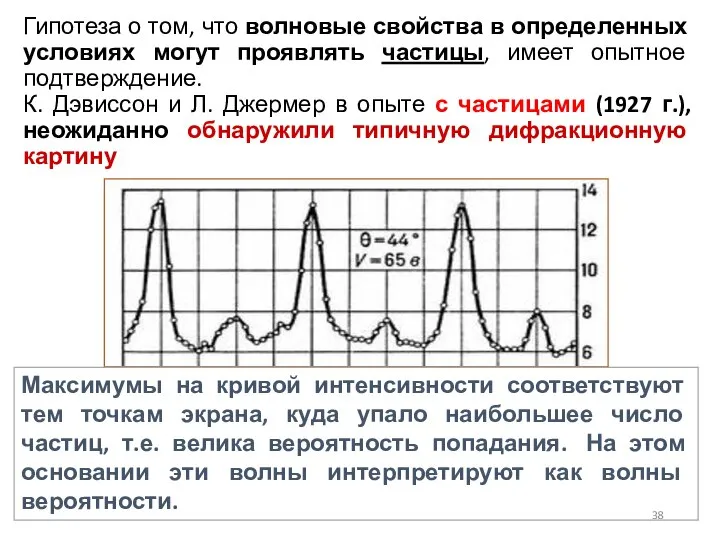
- 38. Гипотеза о том, что волновые свойства в определенных условиях могут проявлять частицы, имеет опытное подтверждение. К.
- 39. Дифракция - свидетельство особого волнового процесса, который в данном случае порождается движущимися частицами (напр., электронами) Природа
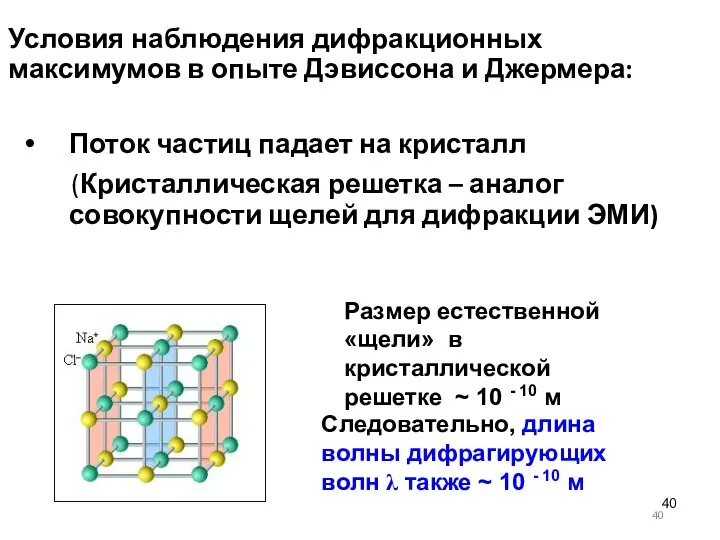
- 40. Условия наблюдения дифракционных максимумов в опыте Дэвиссона и Джермера: Поток частиц падает на кристалл (Кристаллическая решетка
- 41. Особенности дифракции частиц Итак, экспериментально доказано, что при движении любых микрочастиц проявляются волновые свойства. Эффект наблюдается
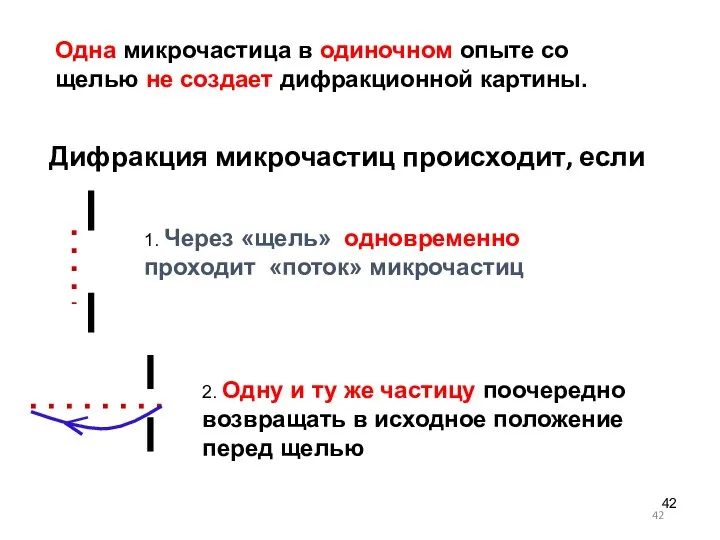
- 42. Дифракция микрочастиц происходит, если 1. Через «щель» одновременно проходит «поток» микрочастиц 2. Одну и ту же
- 43. ВАЖНО! Волновые свойства возникают только в коллективе N одинаковых событий, происходящих в одних и тех же
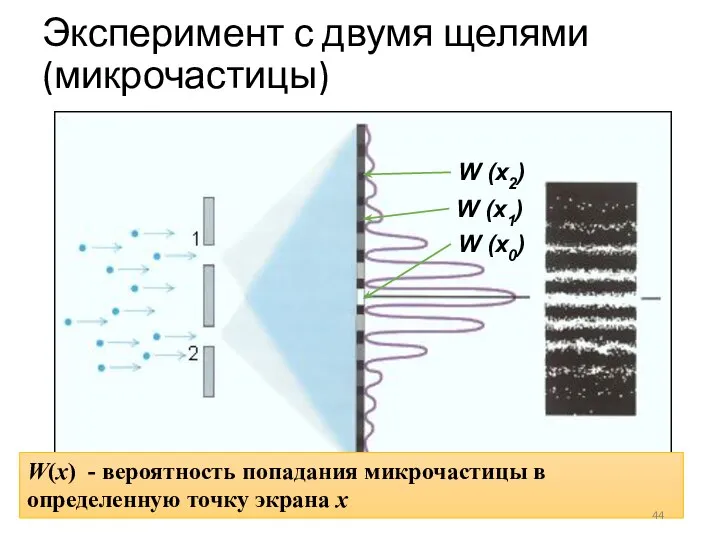
- 44. Эксперимент с двумя щелями (микрочастицы) W (x1) W (x2) W (x0) W(x) - вероятность попадания микрочастицы
- 45. Ансамбль квантонов описывается вероятностным образом через величину Ψ(x) Ψ(x) - амплитуда вероятности, или волновая функция. Ψ(x)
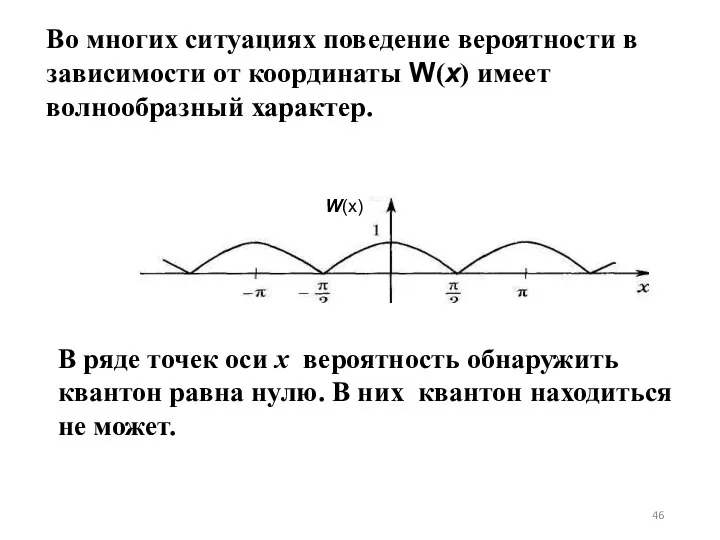
- 46. Во многих ситуациях поведение вероятности в зависимости от координаты W(х) имеет волнообразный характер. В ряде точек
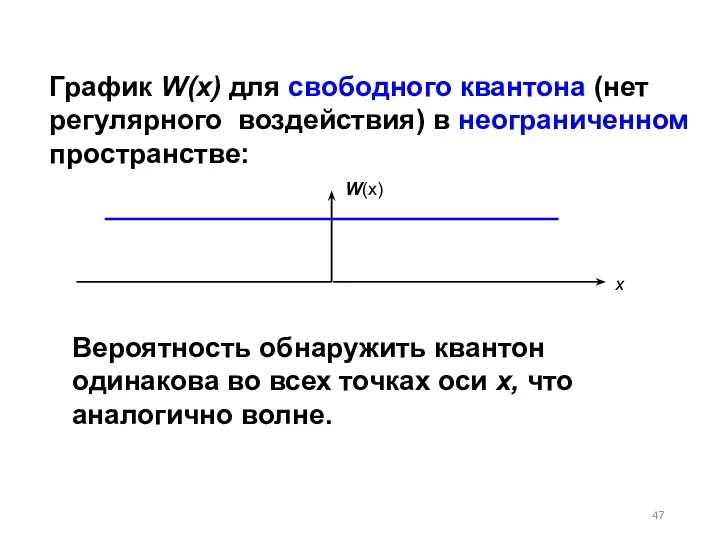
- 47. График W(x) для свободного квантона (нет регулярного воздействия) в неограниченном пространстве: W(x) x Вероятность обнаружить квантон
- 48. Как узнать вероятность W(x)? 1. Определить из опыта; 2. Вычислить теоретически, решая знаменитое уравнение, предложенное Э.Шредингером.
- 49. Особенность квантовых состояний: Квантон может одновременно находиться в нескольких квантовых состояниях: и в состоянии |1› и
- 50. Парадокс кота Шрёдингера Пока атом не распался, с котом всё в порядке, В закрытом ящике находится
- 51. Далее вступает в силу вероятностный характер квантового состояния. Неизвестно, когда атом распадётся. В каждый данный момент
- 52. С другой стороны, когда атом распадается, срабатывает счётчик; по его сигналу молоток разбивает ампулу, и кот
- 53. Возникающий nonsense является парадоксом лишь для макроскопического тела, каким является кот подходя к закрытому ящику, мы
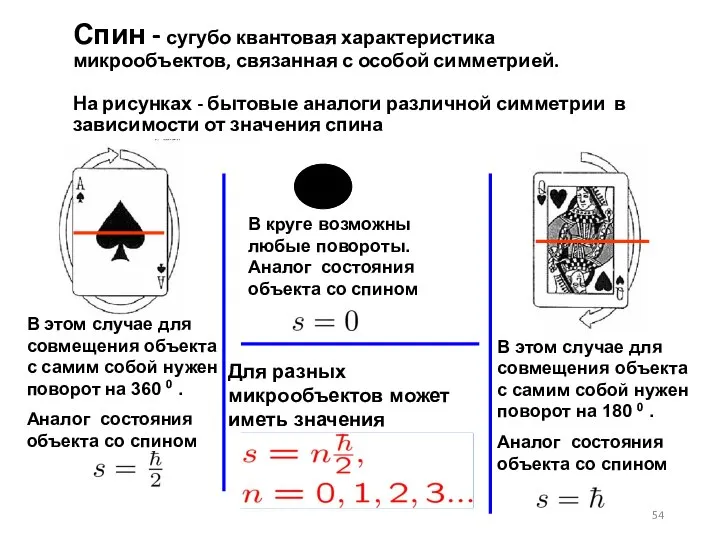
- 54. Спин - сугубо квантовая характеристика микрообъектов, связанная с особой симметрией. На рисунках - бытовые аналоги различной
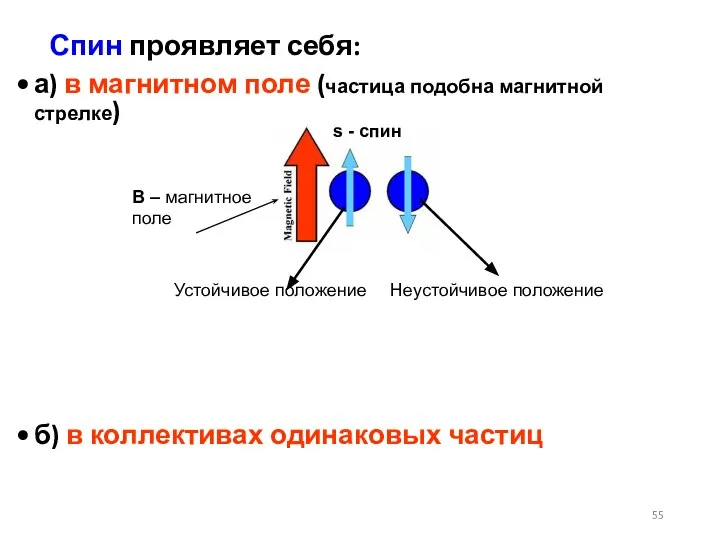
- 55. Спин проявляет себя: а) в магнитном поле (частица подобна магнитной стрелке) б) в коллективах одинаковых частиц
- 56. В зависимости от величины спина микрообъекты делятся на бозоны (фотоны и другие переносчики фунламентальных взаимодействий с
- 57. Особенность поведения бозонов Бозоны с полностью идентичными характеристиками могут пребывать в одном и том же квантовом
- 58. Особенность поведения фермионов Два и более фермиона с полностью идентичными характеристиками не могут одновременно находиться в
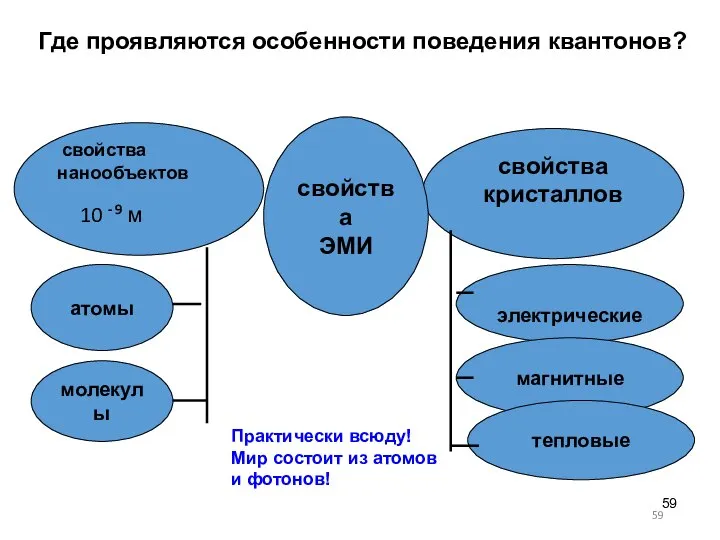
- 59. свойства нанообъектов 10 - 9 м тепловые атомы молекулы свойства ЭМИ Где проявляются особенности поведения квантонов?
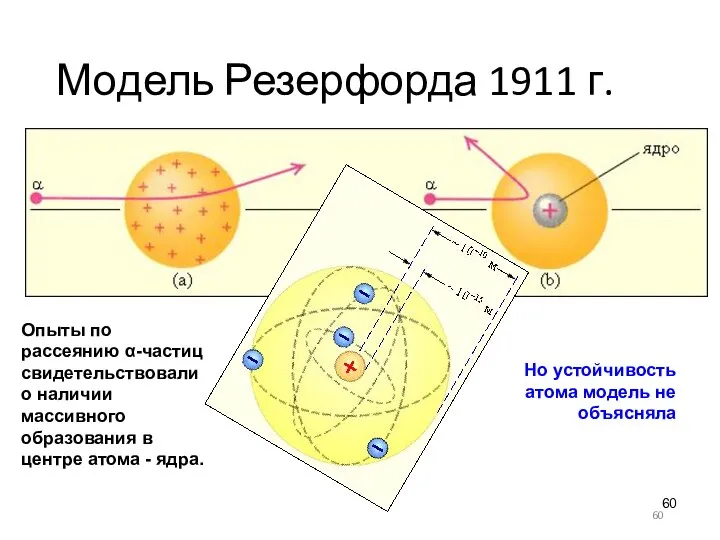
- 60. Модель Резерфорда 1911 г. Опыты по рассеянию α-частиц свидетельствовали о наличии массивного образования в центре атома
- 61. Нильс Бор (1885 - 1962 ) датский ученый, один из создателей современной физики. Автор основополагающих трудов
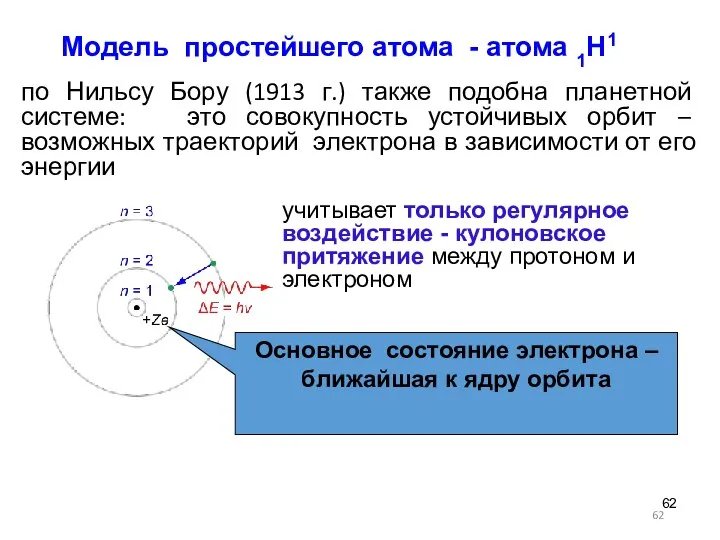
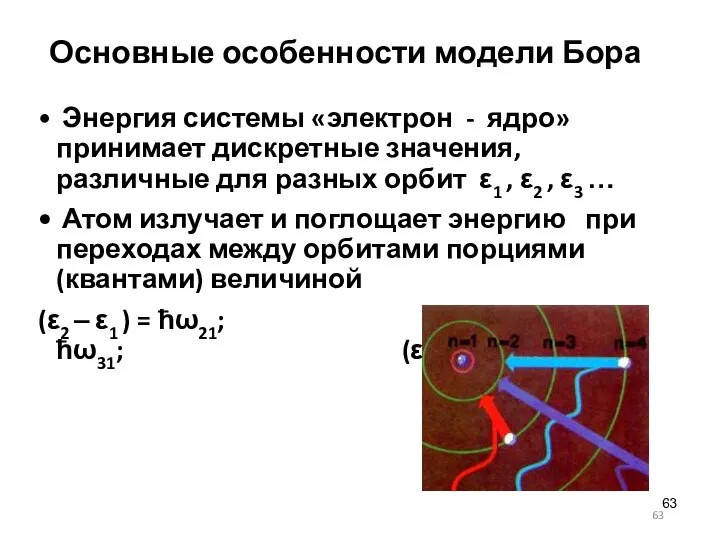
- 62. по Нильсу Бору (1913 г.) также подобна планетной системе: это совокупность устойчивых орбит – возможных траекторий
- 63. Основные особенности модели Бора Энергия системы «электрон - ядро» принимает дискретные значения, различные для разных орбит
- 64. Модель Бора сочетает классические и неклассические положения - учитывает только регулярное воздействие - кулоновское притяжение между
- 65. Современная модель атома водорода как решение уравнения Шрёдингера ОСОБЕННОСТИ: Учитывает стохастическое воздействие на электрон со стороны
- 66. Вероятность обнаружить электрон на разных расстояниях от ядра в основном состоянии Под кривыми - области, недоступные
- 67. Конфигурации вероятности нахождения электрона в атоме 1Н1
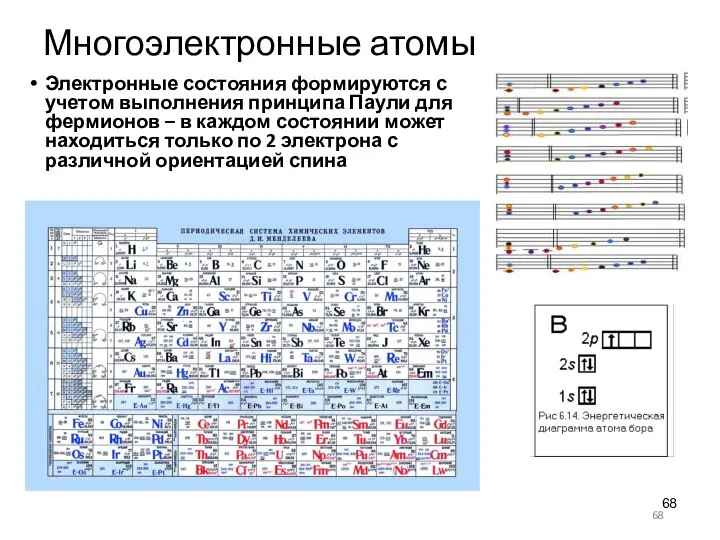
- 68. Многоэлектронные атомы Электронные состояния формируются с учетом выполнения принципа Паули для фермионов – в каждом состоянии
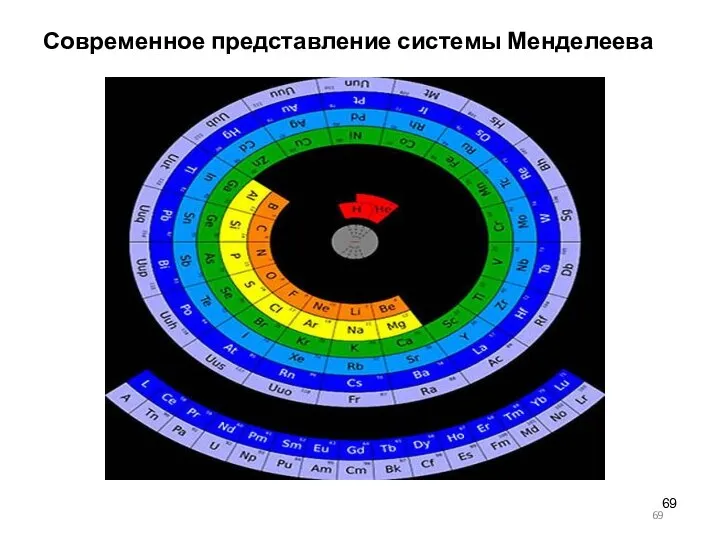
- 69. Современное представление системы Менделеева
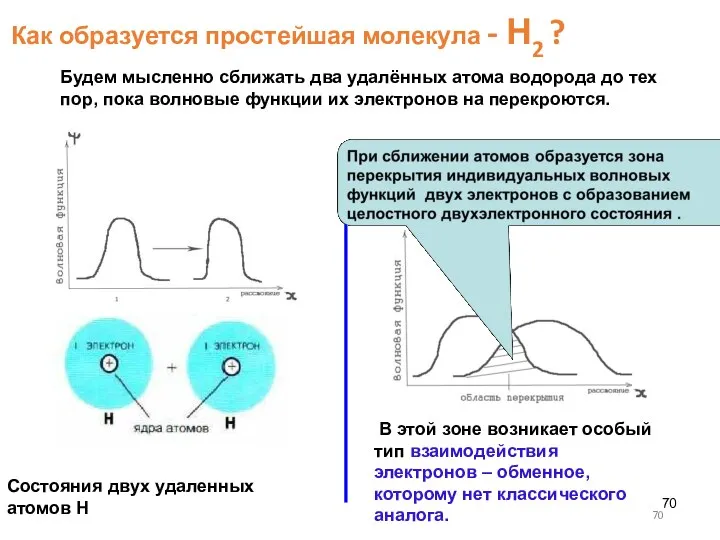
- 70. Как образуется простейшая молекула - Н2 ? Состояния двух удаленных атомов Н В этой зоне возникает
- 71. Оно зависит от взаимной ориентации спинов электронов. При антипараллельных спинах оно имеет характер притяжения, что и
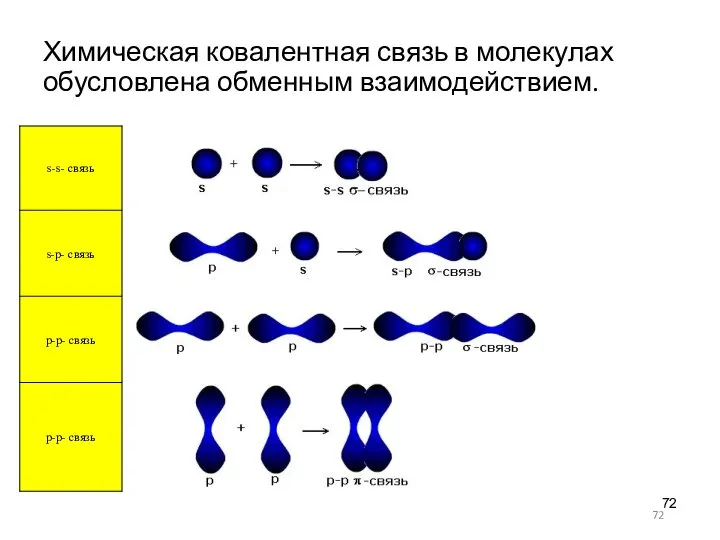
- 72. Химическая ковалентная связь в молекулах обусловлена обменным взаимодействием.
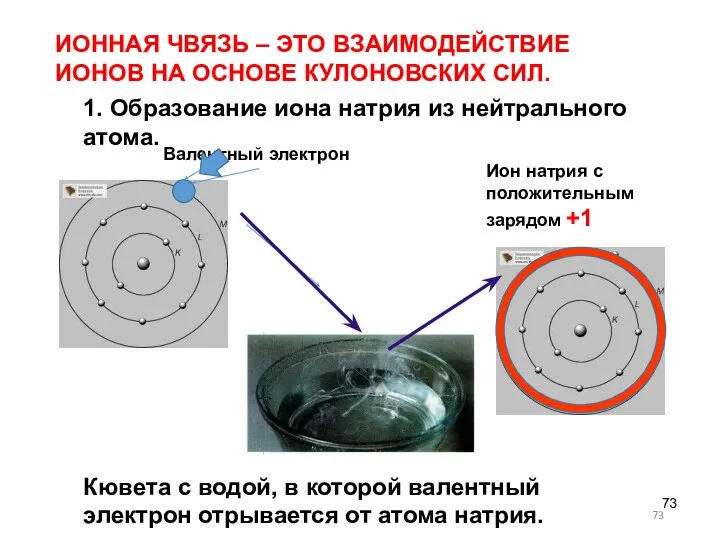
- 73. 1. Образование иона натрия из нейтрального атома. Валентный электрон Ион натрия с положительным зарядом +1 Кювета
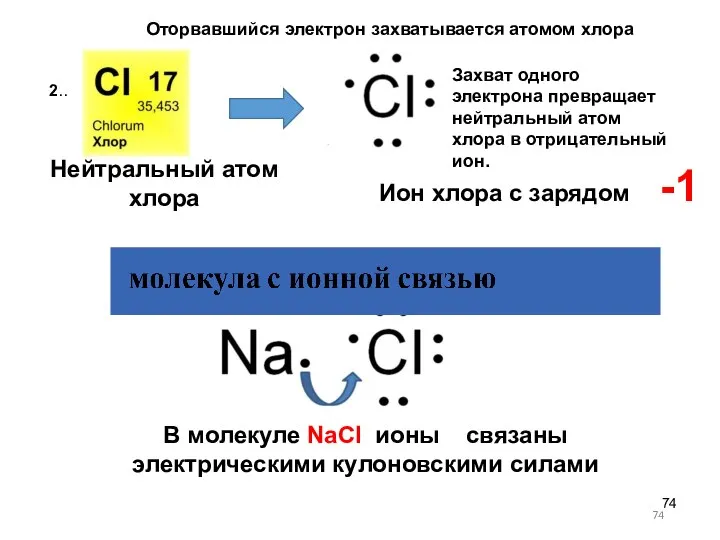
- 74. Нейтральный атом хлора Ион хлора с зарядом -1 В молекуле NaCl ионы связаны электрическими кулоновскими силами
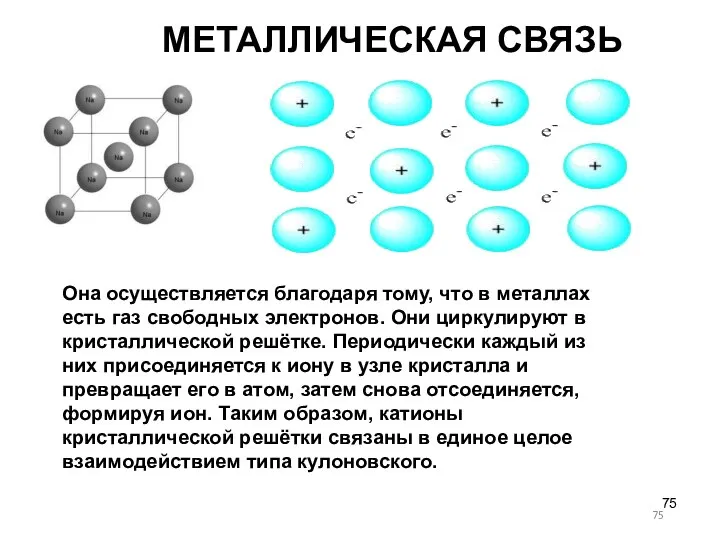
- 75. МЕТАЛЛИЧЕСКАЯ СВЯЗЬ Она осуществляется благодаря тому, что в металлах есть газ свободных электронов. Они циркулируют в
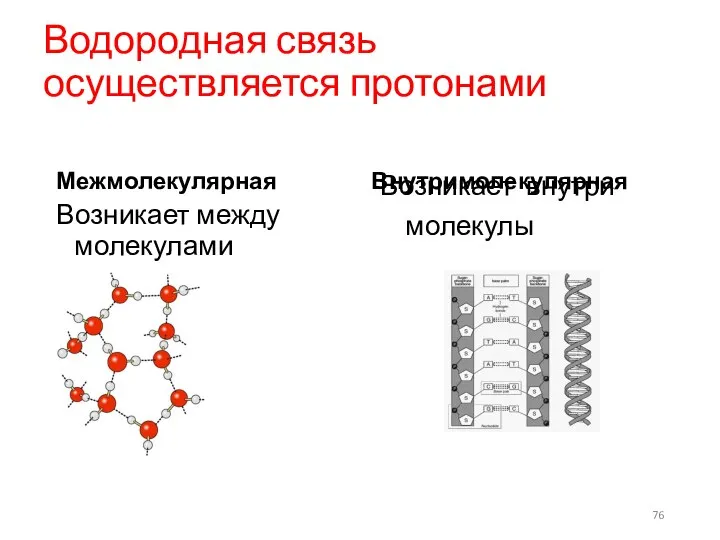
- 76. Водородная связь осуществляется протонами Межмолекулярная Возникает между молекулами Внутримолекулярная Возникает внутри молекулы
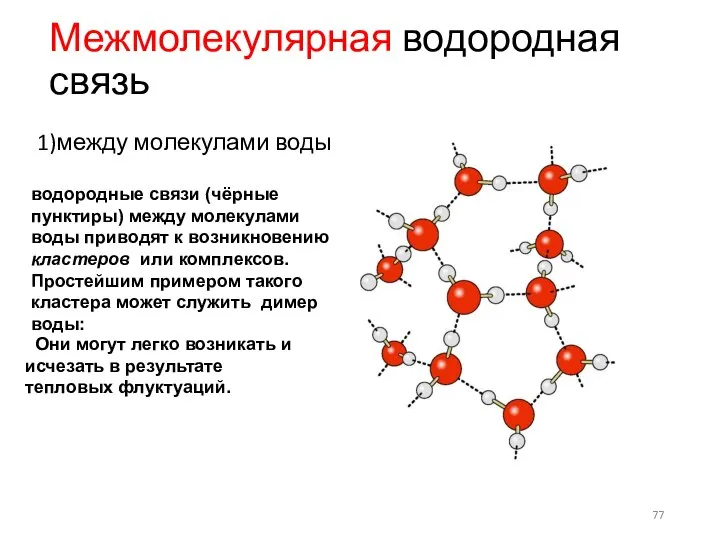
- 77. Межмолекулярная водородная связь 1)между молекулами воды водородные связи (чёрные пунктиры) между молекулами воды приводят к возникновению
- 78. Межмолекулярные водородные связи способствуют образованию кристаллов в виде снежинок или измороси
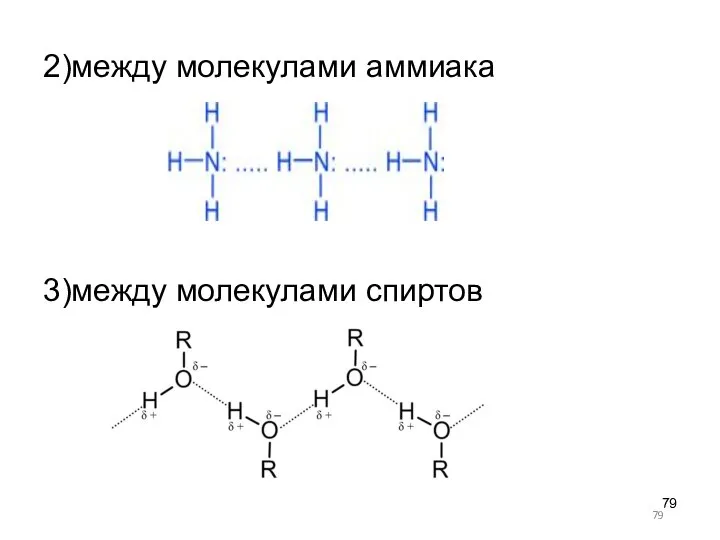
- 79. 2)между молекулами аммиака 3)между молекулами спиртов
- 80. Внутримолекулярная водородная связь возникает 1)внутри молекул белков (водородная связь удерживает витки спирали пептидной молекулы)
- 82. Скачать презентацию












































 Электроснабжение многофункционального торгово-развлекательного центра в г. Сегежа
Электроснабжение многофункционального торгово-развлекательного центра в г. Сегежа Сила
Сила Простые механизмы. Рычаг
Простые механизмы. Рычаг Водяные бомбочки
Водяные бомбочки Электростатика
Электростатика Что изучает физика? (7 класс)
Что изучает физика? (7 класс) Иондық каландар мен тасымалдаушылар кұрылысы мен қызметі. Электрогенез механизмі
Иондық каландар мен тасымалдаушылар кұрылысы мен қызметі. Электрогенез механизмі Делимость электрического заряда. Электрон. Строение атома
Делимость электрического заряда. Электрон. Строение атома Статика и димамика
Статика и димамика Ford Focus II. Задняя подвеска
Ford Focus II. Задняя подвеска Оптика и основы микроскопии
Оптика и основы микроскопии Принципы и методы обработки результатов измерения физических величин
Принципы и методы обработки результатов измерения физических величин Презентация на тему Собирающие линзы
Презентация на тему Собирающие линзы  Цилиндрические прямозубые передачи
Цилиндрические прямозубые передачи Солнечное излучение как совокупность ресурсов
Солнечное излучение как совокупность ресурсов Теплоприемник. Упрощение устройства при одновременном повышении точности измерения
Теплоприемник. Упрощение устройства при одновременном повышении точности измерения Электрическое сопротивление
Электрическое сопротивление Сила Архимеда
Сила Архимеда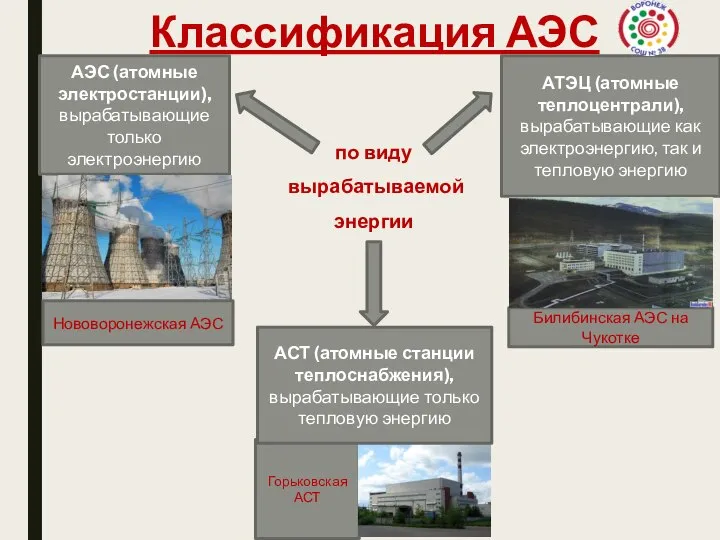 Классификация АЭС
Классификация АЭС Электростатика
Электростатика Дифференциальный подход
Дифференциальный подход Поверхностное натяжение
Поверхностное натяжение Электрические цепи переменного тока
Электрические цепи переменного тока Динамика моря и Условия судоходства
Динамика моря и Условия судоходства Молния
Молния Источники радиоактивных загрязнений
Источники радиоактивных загрязнений Презентация на тему Напряженность электрического поля. Принцип суперпозиции электрических полей
Презентация на тему Напряженность электрического поля. Принцип суперпозиции электрических полей  Механические колебания
Механические колебания