Содержание
- 2. 1.Сила тяжести как равнодействующая вертикальных сил. 2.Центр тяжести. Методы нахождения. 3. Центр тяжести простых геометрических фигур
- 3. 1.Сила тяжести как равнодействующая вертикальных сил.
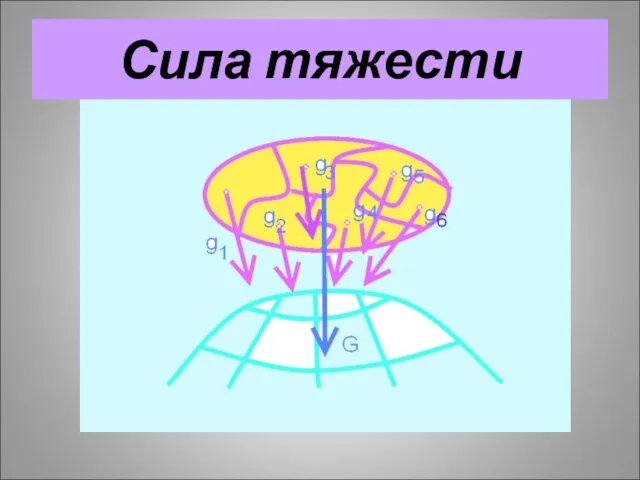
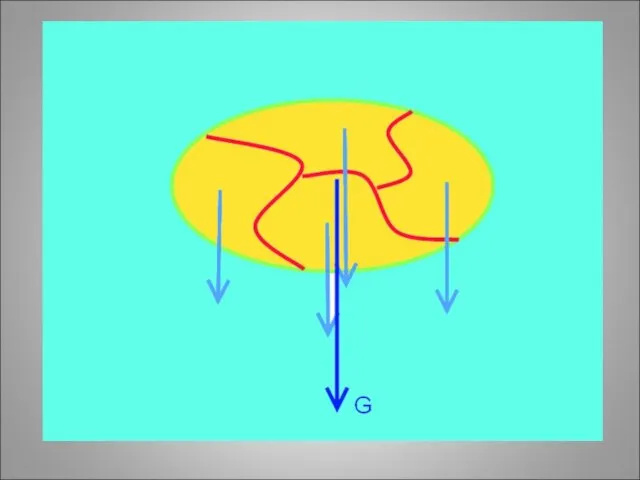
- 7. G – сила тяжести. Сила тяжести – это сила, с которой тела притягиваются к земле Сила
- 8. Сила тяжести
- 10. 2.Центр тяжести. Методы нахождения
- 11. Центр тяжести тела – это такая неизменно связанная с этим телом точка, через которую проходит линия
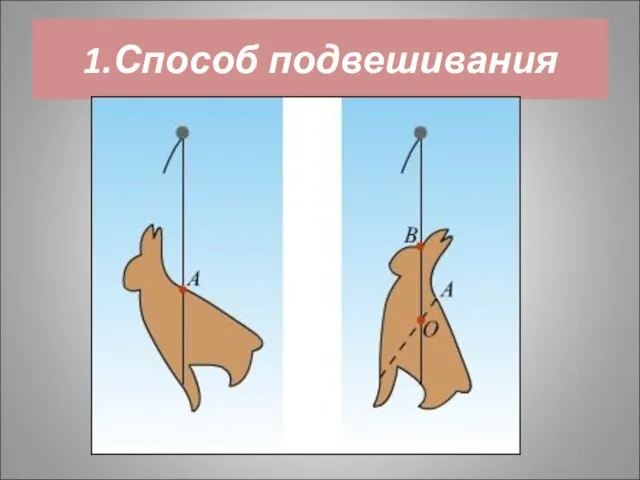
- 12. Методы определения центра тяжести тела - Способ подвешивания; - Способ взвешивания; - Аналитический способ.
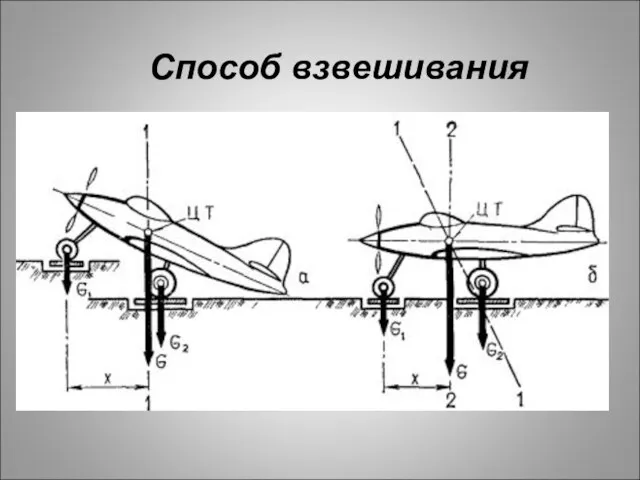
- 13. Способ взвешивания
- 14. Способ взвешивания
- 15. Аналитический способ 1 Метод симметрии 2 Метод разделения (разбиения) 3 Метод отрицательных масс
- 16. . 1 Метод симметрии 1.1 Если однородное тело имеет плоскость симметрии, то центр тяжести лежит в
- 17. 1.2 Если однородное тело имеет ось симметрии, то центр тяжести лежит на этой оси. Центр тяжести
- 18. 2 Метод разделения (разбиения) Тело разбивается на наименьшее число частей, силы тяжести и положение центров тяжести
- 19. 3 Метод отрицательных масс При определении центра тяжести тела, имеющего свободные полости, следует применять метод разбиения,
- 20. Xc, Yc, Zc – координаты центра тяжести тела; Xi ,Yi , Zi – координаты i- ой
- 21. 3.Центр тяжести простых геометрических фигур
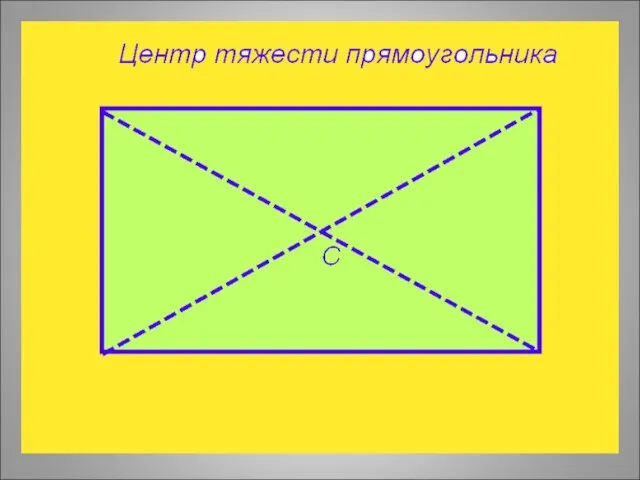
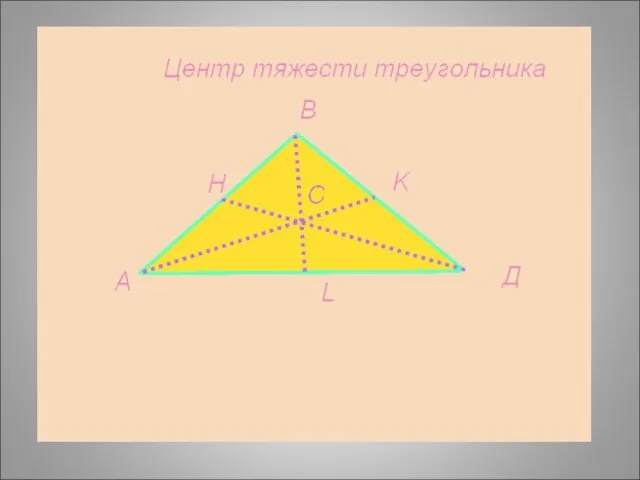
- 22. Координаты центра тяжести плоской фигуры
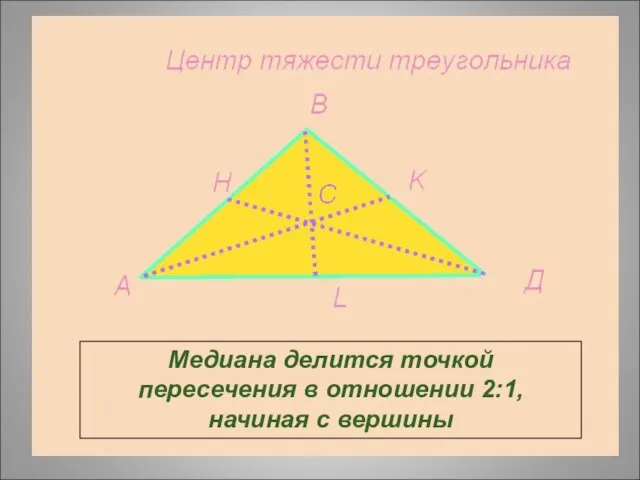
- 25. Медиана делится точкой пересечения в отношении 2:1, начиная с вершины
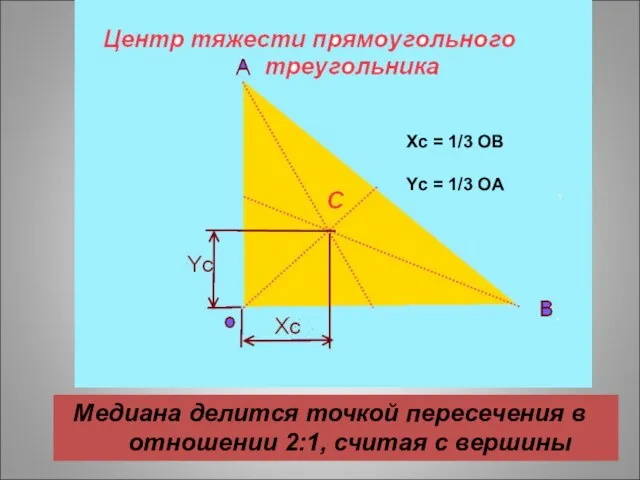
- 27. Медиана делится точкой пересечения в отношении 2:1, считая с вершины Xc = 1/3 OB Yc =
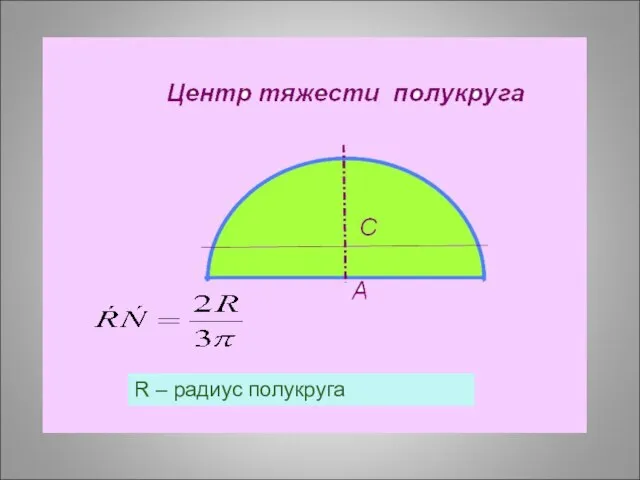
- 29. R – радиус полукруга
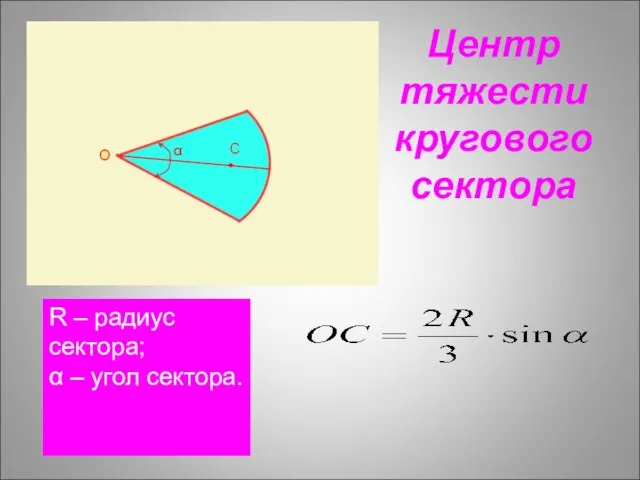
- 30. Центр тяжести кругового сектора R – радиус сектора; α – угол сектора.
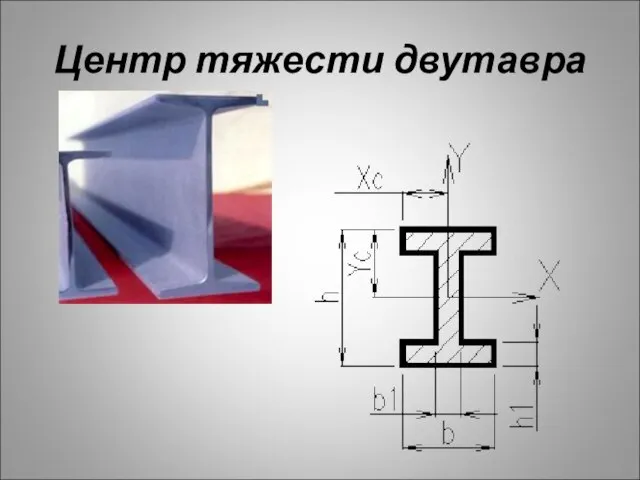
- 32. Центр тяжести двутавра
- 34. Центр тяжести швеллера
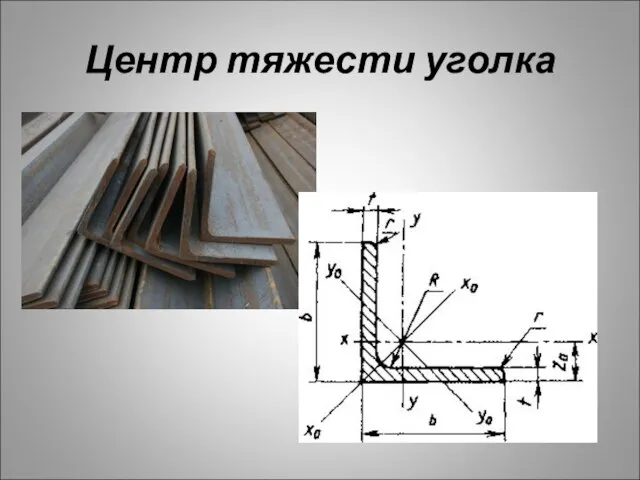
- 36. Центр тяжести уголка
- 37. Определение центра тяжести фигуры неправильной формы. 1) Метод подвешивания на острие; 2) Теоретический метод
- 38. 1.Способ подвешивания
- 39. 2. Теоретический метод В этом случае сложная фигура разбивается на определенное количество элементарных фигур, имеющих правильную
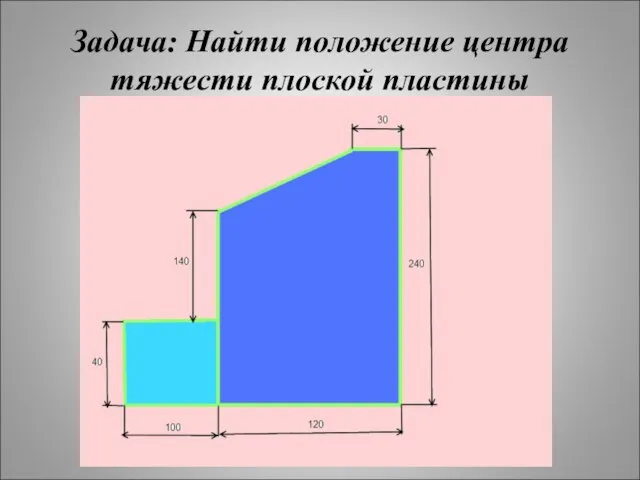
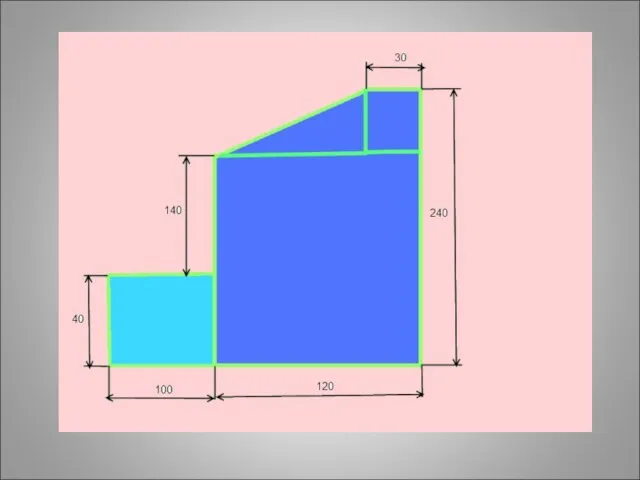
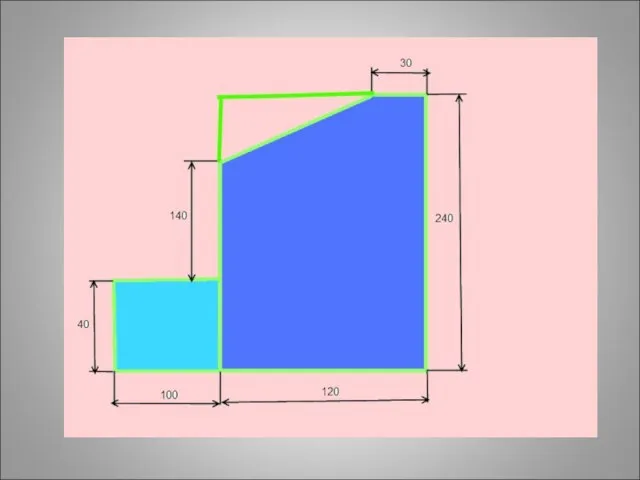
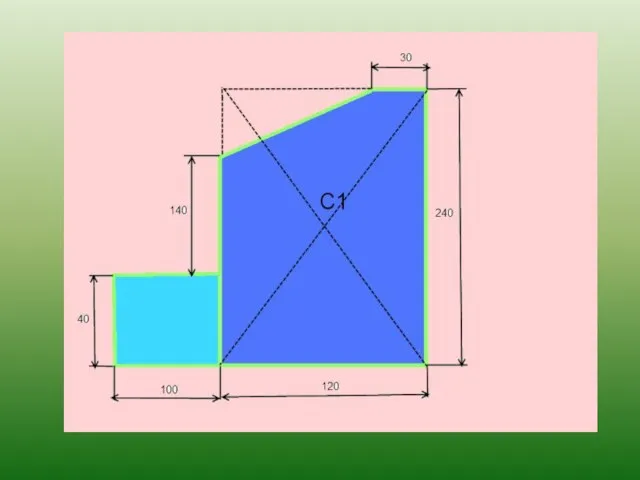
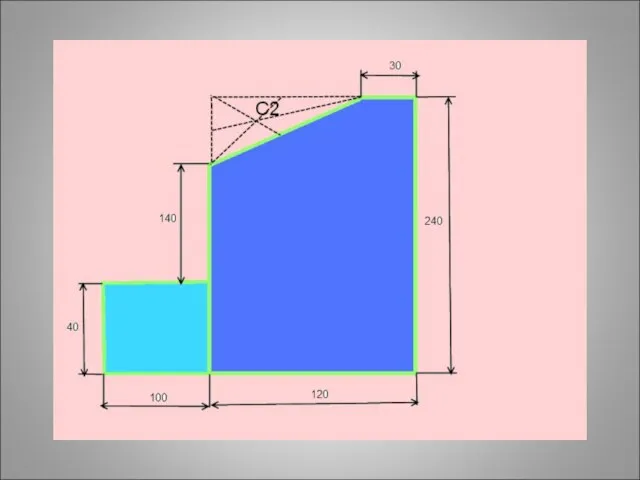
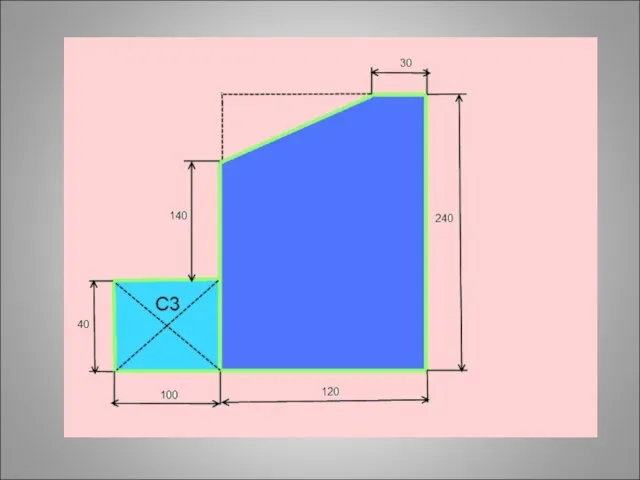
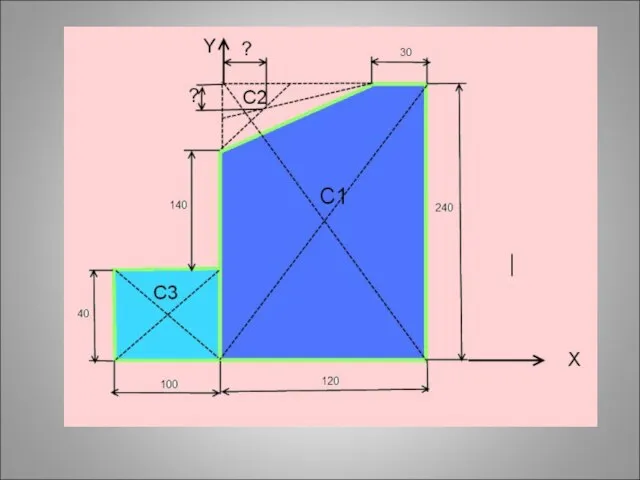
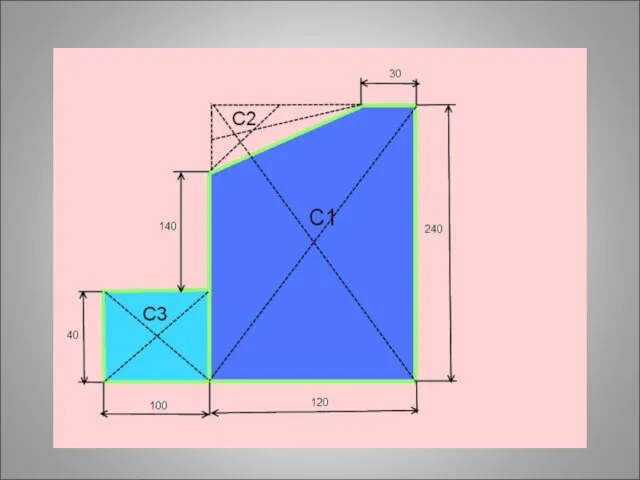
- 40. Задача: Найти положение центра тяжести плоской пластины
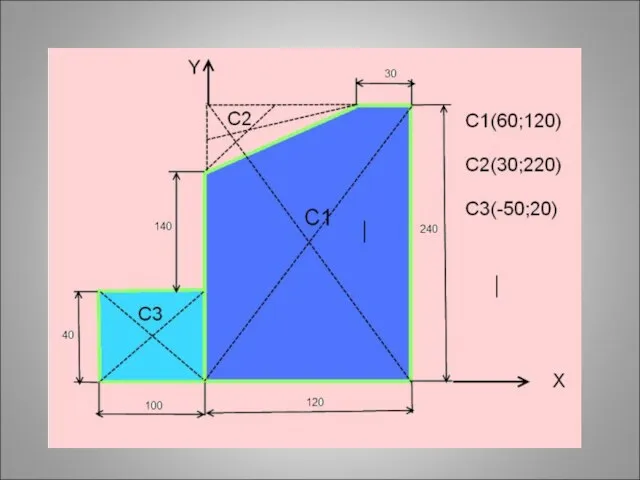
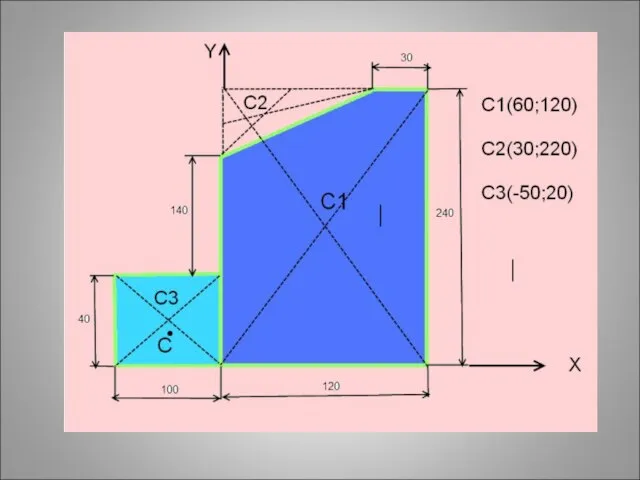
- 49. 1)Прямоугольник А1 = 10*4 = 40 см2 С1(6;12) 2) Прямоугольник А2 = 12*24 = 288 см2
- 50. 1)Прямоугольник А1 = 10*4 = 40 см2 С1(6;12) 2) Прямоугольник А2 = 12*24 = 288 см2
- 52. 1. Сегодняшний урок мне (понравился или не понравился) 2. Мне понравилось …(назвать, что именно) 3. Пригодятся
- 54. Скачать презентацию




























 Насыщенный пар. Кипение. Влажность воздуха. Уроки физики в 10 классе
Насыщенный пар. Кипение. Влажность воздуха. Уроки физики в 10 классе Архимедова сила. Решение задач
Архимедова сила. Решение задач Прямолинейное равноускоренное движение. Ускорение
Прямолинейное равноускоренное движение. Ускорение Характеристики электрического тока
Характеристики электрического тока Классификация методов хроматографии
Классификация методов хроматографии Деление ядер урана
Деление ядер урана Внутренняя энергия
Внутренняя энергия Оптические игрушки
Оптические игрушки еометрическая оптика
еометрическая оптика Презентация на тему Единицы силы. Связь между силой тяжести и массой тела
Презентация на тему Единицы силы. Связь между силой тяжести и массой тела  Учебно-научный образовательный комплекс для учащихся школ, лицеев, студентов и магистрантов
Учебно-научный образовательный комплекс для учащихся школ, лицеев, студентов и магистрантов Применение ядерной энергии в различных отраслях. Доза радиоактивного излучения
Применение ядерной энергии в различных отраслях. Доза радиоактивного излучения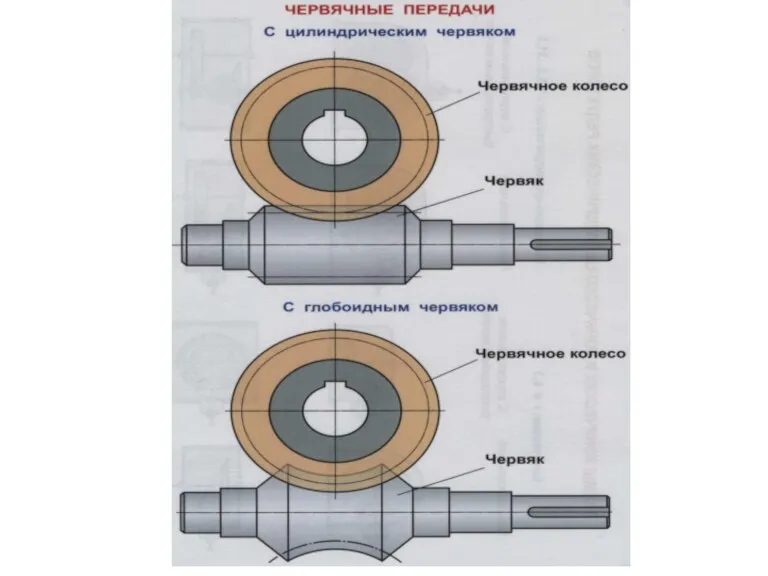 Червячные передачи
Червячные передачи Электромагниты и их применение
Электромагниты и их применение Полная работа системы
Полная работа системы Опорные конспекты по физике. Механика. 9 класс
Опорные конспекты по физике. Механика. 9 класс Управление потоком поверхностных плазмонполяритонов с помощью внешних полей
Управление потоком поверхностных плазмонполяритонов с помощью внешних полей Механические колебания и волны. Звук. Решение заданий ОГЭ
Механические колебания и волны. Звук. Решение заданий ОГЭ Основы структурного анализа сигналов
Основы структурного анализа сигналов Электрический ток в различных средах
Электрический ток в различных средах Плазма и её использование
Плазма и её использование Трансформатор в физике
Трансформатор в физике Электромагнетизм
Электромагнетизм Построение теоретического профиля кулачка
Построение теоретического профиля кулачка Фізика. Запитання для оцінювання
Фізика. Запитання для оцінювання Критерии прочности намоточных труб при растяжении, кручении и сложном напряженном состоянии
Критерии прочности намоточных труб при растяжении, кручении и сложном напряженном состоянии Спектр электромагнитных волн
Спектр электромагнитных волн Презентация на тему Механическое движение
Презентация на тему Механическое движение