Электричество и магнетизм (лекция 11)

Электростатика и магнитостатика
Основные законы для векторных полей, не меняющихся со временем (постоянные поля)

Электростатика и магнитостатика
Поток вектора через замкнутую поверхность
Если площадка dS дифференциально мала («точечная»), то элементарный поток вектора u через нее dФ = (u,dS) Вектор dS считаем направленным по нормали к площадке.
Поток вектора Ф через большую поверхность S вычисляется как сумма (интеграл) элементарных потоков ΔФ через все микроскопические площадки dS , составляющие большую.
Нормали для замкнутой поверхности считаются направленными изнутри наружу.
Поток пропорционален числу силовых линий поля, пронизыва.щих площадку (с учетом их направления)

Электростатика и магнитостатика
Дивергенция вектора в данной точке
Дивергенция вектора в данной точке
= предел отношения потока вектора через дифференциально малую поверхность вблизи этой точки к объёму, заключенному внутри этой малой поверхности;
= сумма производных компонент вектора А по соответствующим координатам.
div E =
div B =
divE = dФ/dV = (Σ qi / ɛ0 )dV = ρ / ɛ0
divA = dФA /dV = дAx /дx + дAy /дy + дAz /дz

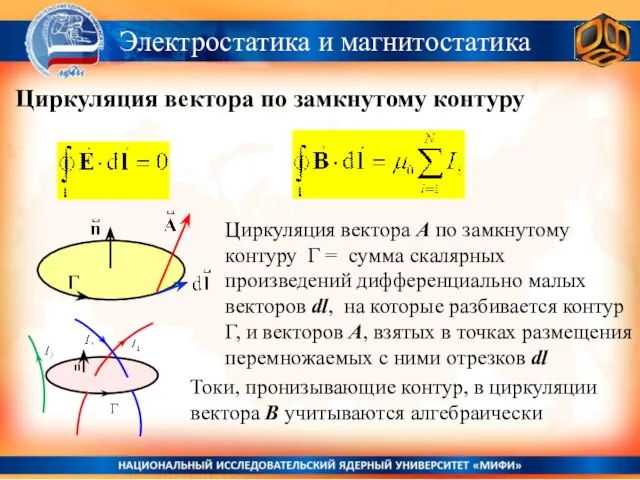
Электростатика и магнитостатика
Циркуляция вектора по замкнутому контуру
Циркуляция вектора А по замкнутому контуру Г = сумма скалярных произведений дифференциально малых векторов dl, на которые разбивается контур Г, и векторов А, взятых в точках размещения перемножаемых с ними отрезков dl
Токи, пронизывающие контур, в циркуляции вектора В учитываются алгебраически

Электростатика и магнитостатика
Ротор вектора в точке
rot E =
rot B =
(rotA)x= dCirA,x /dSГх = дAz /дy - дAy /дz
(rotA)y= dCirA,y /dSГy = дAx /дz - дAz /дx
(rotA)z= dCirA,z /dSГz = дAy /дx - дAx /дy
rot А – вектор, компоненты которого равны пределам отношений циркуляций вектора А по дифференциально малым контурам Гх,y,z вблизи точки вычисления ротора, расположенным в плоскостях, перпендикулярных соответствующим координатным компонентам. Компоненты ротора вычисляются как разности производных от вектора А, подобно тому, как вычисляются компоненты векторного произведения.

Векторное поле называется вихревым, если ротор этого поля не равен нулю тождественно во всех точках.
Электростатика и магнитостатика
Ротор вектора и его компоненты

Замечание 1. Магнитное поле является вихревым, поскольку его ротор НЕ равен нулю тождественно.
Замечание 2. Любое векторное вихревое поле (в частности – магнитное В) можно представить в виде ротора другой векторной функции:
здесь вектор А называют векторным потенциалом магнитного поля. Для магнитного поля, создаваемого точечным равномерно движущимся зарядом В = (μ0/4π)q[v,r]/r3
A = (μ0/4π)qv/r = μ0ε0φv = φv/с2
μ0ε0 = 1/с2 (!!!)
ДЗ: проверить формулу!
Электростатика и магнитостатика

Основные законы электростатики и магнитостатики
Электростатика и магнитостатика

Магнитный диполь
Точечный магнитный диполь
контур с током I, дифференциально малой площади S. Магнитный дипольный момент (определение): pm = ISn
Направление нормали n и дипольного момента pm определяется Правилом Правого Винта.

Магнитный диполь
Магнитное поле точечного магнитного диполя
Магнитный дипольный момент
Линии магнитной индукции магнитного диполя

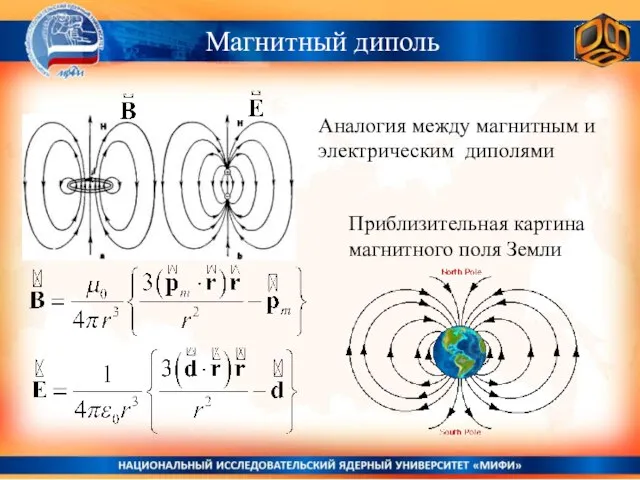
Аналогия между магнитным и электрическим диполями
Приблизительная картина магнитного поля Земли
Магнитный диполь

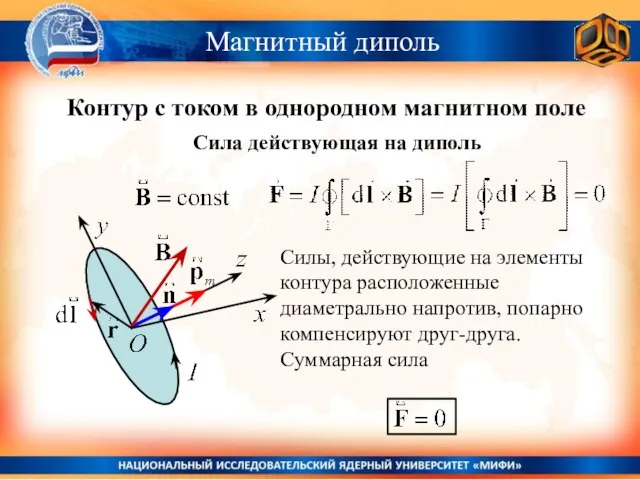
Контур с током в однородном магнитном поле
Магнитный диполь
Сила действующая на диполь
Силы, действующие на элементы контура расположенные диаметрально напротив, попарно компенсируют друг-друга. Суммарная сила

Контур с током в однородном магнитном поле
Магнитный диполь
Моменты сил, действующих на элементы контура
dFЛ = I[dl, B]

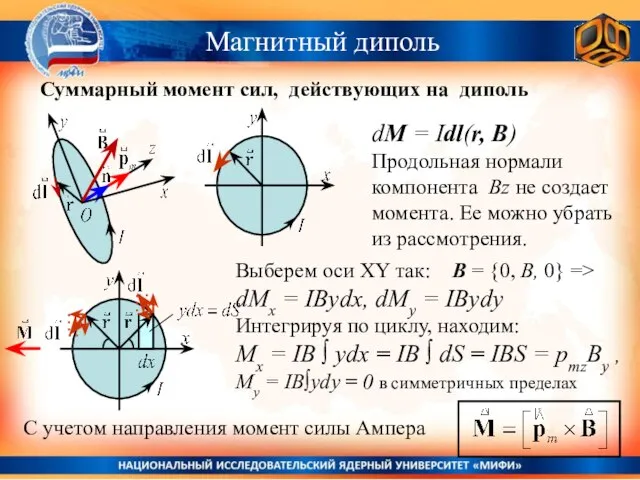
Магнитный диполь
Суммарный момент сил, действующих на диполь
dM = Idl(r, B)
Продольная нормали компонента Вz не создает момента. Ее можно убрать из рассмотрения.
Выберем оси XY так: В = {0, B, 0} =>
dMx = IBydx, dMy = IBydy
Интегрируя по циклу, находим:
Mx = IB ∫ ydx = IB ∫ dS = IBS = pmzBy ,
My = IB∫ydy = 0 в симметричных пределах
С учетом направления момент силы Ампера

Магнитный диполь
Механическая энергия магнитного диполя
dw = dA
Момент силы Ампера поворачивает рамку с током так, чтобы ее нормаль совпала по направлению с B. Это самое энергетически выгодное состояние – с минимальной потенциальной энергией.

Контур с током в неоднородном магнитном поле
Магнитный диполь
Сила действующая на диполь
Формулы для момента силы и энергии магнитного диполя одинаковы для однородного и неоднородного полей.
Как правило свободный магнитный диполь втягивается в область более сильного магнитного поля.

Спасибо за внимание!
Дистанционный курс общей физики НИЯУ МИФИ
Следующая лекция
17 ноября

Природа парамагнетизма
Что поле В может делать с атомами среды, если каждый – практически точечный магнитный диполь (или сумма нескольких совмещенных диполей?
1. Может пытаться повернуть моменты в свою сторону. Поле при этом усилится!
Тепловое движение препятствует этому усилению.

Ферромагнетизм
Групповое взаимодействие атомов в некоторых веществах (ферромагнетики с доменной структурой) может значительно усилить эффект со-ориентации магнитных моментов.

Природа диамагнетизма
2. Поле может заставить электроны в атомах прецессировать подобно «раскрученным волчкам» вокруг направления вектора В. При этом поле прецессирующих волчков будет направлено против внешнего, которое ослабнет)
Этому эффекту больше подвержены атомы, собственные моменты которых скомпенсированы (= 0):

Магнетики
Магнетики: вещества, способные в той или иной степени намагничиваться во внешнем магнитном поле и менять величину этого поля. .
В изотропном магнетике: B = μB0 ; B’ = χB0
χ - магнитная восприимчивость
μ = 1 + χ - магнитная проницаемость
Магнитное поле в магнетиках может быть как слабее, так и сильнее, чем оно было-бы в вакууме. Соответственно, значения μ могут быть как больше, так и меньше единицы.

Классификация магнетиков
Парамагнетики – вещества, приобретающие магнитный момент сонаправленный с внешним магнитным полем и усиливающий его
μпара >1 (~1,000xxx) ; χ пара << 1 (~10-4)
Диамагнетики – вещества, приобретающие в поле магнитный момент, направленный против внешнего магнитного поля
μдиа < 1 (~0, 999xxx)
χ диа <0; |χ диа | << 1 (~10-4)

Классификация магнетиков
Ферромагнетики) – вещества с доменной структурой, приобретающие магнитный момент , сонаправленный с внешним магнитным полем и значительно усиливающий его
μферро >>1 (~103)

Периодическая таблица элементов, показывающая различные типы намагничивания при комнатной температуре.
Магнетики

Диамагнетики
Левитация пиролитического углерода
Левитация живой лягушки в поле 16Тл
(Андрей Гейм и Майкл Берри – «Шнобелевская» премия (IgNoble Prize) 2000 г.)

Магнитное поле в среде
Для описания магнитного поля в средах (в магнетиках) используют не только м вектор магнитной индукции В. измеряемой в Тл (Тесла), но также и вектор напряженности магнитного поля H. Измеряемый в А/м
В вакууме B = μ0H.
μ0 = 4π·10-7 Н/А2 – магнитная постоянная
В изотропной среде B = μμ0H.
Аналогия с электрическим полем:
в вакууме D = ε0E. в изотропной среде D = εε0 Е.

Спасибо за внимание!
Дистанционный курс общей физики НИЯУ МИФИ
Следующая лекция
17 ноября

Магнетики
Магнетики - вещества, способные в той или иной степени намагничиваться во внешнем магнитном поле. Различаются величинами магнитной проницаемости μ и магнитной восприимчивости χ = μ - 1
Диамагнетики: χ<0. μ <~ 1
Парамагнетики: χ>0. μ >~ 1
Ферромагнетики: χ>0. μ >>1

Природа парамагнетизма
Эксперимент П. Кюри:
Закон Кюри – Вейса для жидких и твёрдых тел:
1. Магнитная восприимчивость парамагнетиков зависит от температуры
2. Парамагнетиками являются вещества, у которых собственный магнитный момент атомов не равен нулю.

Природа парамагнетизма
При термодинамическом равновесии относительная доля молекул, магнитные моменты которых ориентированы в пределах угла , определяется распределением Больцмана:

Природа диамагнетизма
1. Магнитная восприимчивость диамагнетиков не зависит от температуры (П. Кюри, 1895).
2. Диамагнетиками - вещества, у которых собственный магнитный момент атомов равен нулю.

Ферромагнетизм
Природа ферромагнетизма
Намагничивание ферромагнитных материалов (железо никель и т.п.) возникает благодаря взаимодействию магнитных моментов электронов одной из внутренних оболочек атомов.
В результате такого взаимодействия спины и магнитные моменты этих электронов ориентируются параллельно.
Эффект обусловлен так называемым обменным взаимодействием (неэлектростатической природы).

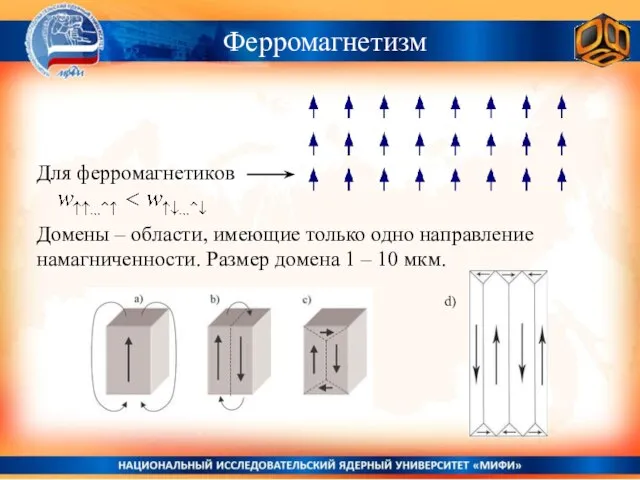
Ферромагнетизм
Домены – области, имеющие только одно направление намагниченности. Размер домена 1 – 10 мкм.
d)

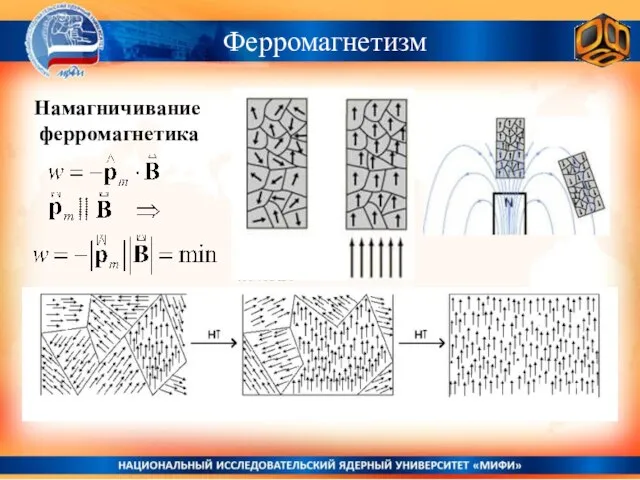
Ферромагнетизм
Намагничивание
ферромагнетика

Ферромагнетизм
Магнитные моменты в ферромагнетиках имеют тенденцию становиться параллельными друг другу под действием приложенного магнитного поля. Однако в отличие от парамагнетиков эти магнитные моменты остаются параллельными после выключения магнитного поля.
Ферромагнетизм

Антиферромагнетизм
Магнитные моменты соседних «магнитных» ионов имеют тенденцию выстроиться антипараллельно по отношению к друг другу в отсутствие приложенного магнитного поля. В простейшем случае соседние магнитные моменты имеют одинаковые по модулю значения, поэтому в среднем намагничивание отсутствует.
Ферромагнетизм

Периодическая таблица элементов, показывающая различные типы намагничивания при комнатной температуре.
Магнетики