Центр тяжести

ТОМИЛИН Александр Константинович
доктор физико-математических наук,
профессор Отделения общетехнических дисциплин
Школы базовой инженерной подготовки
Томского политехнического университета

Лекция 3(2)
Центр тяжести и центр масс

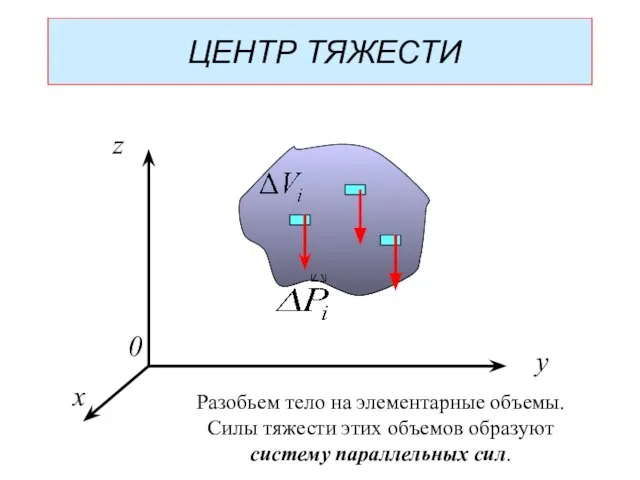
x
y
z
0
ЦЕНТР ТЯЖЕСТИ
Разобьем тело на элементарные объемы.
Силы тяжести этих объемов образуют
систему параллельных сил.

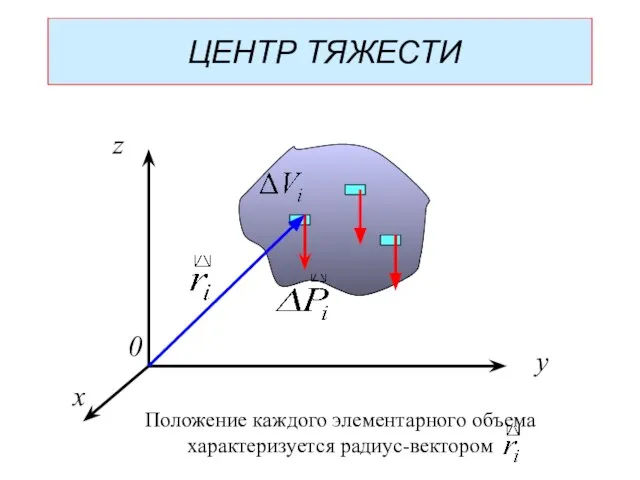
x
y
z
0
ЦЕНТР ТЯЖЕСТИ
Положение каждого элементарного объема характеризуется радиус-вектором

- удельная плотность тела
ускорение свободного падения в данной
точке
(1)
Сила тяжести элементарного объема:

Положение центра тяжести тела определяется
радиус-вектором:

Положение центра тяжести тела определяется
радиус-вектором:
(2)

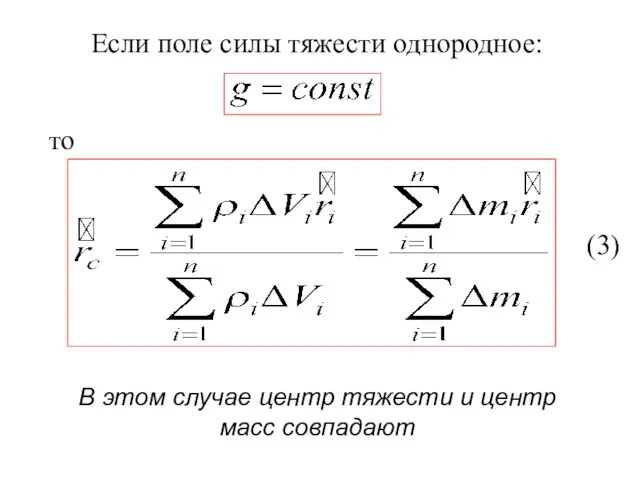
Если поле силы тяжести однородное:
то
В этом случае центр тяжести и центр
масс совпадают
(3)

Центром масс называется центр параллельных
сил, пропорциональных массе

Если требуется определить центр масс дискретной
системы материальных точек:
Центром масс называется центр параллельных
сил, пропорциональных массе

Для сплошных тел:
(4)

Для сплошных тел:
Для сплошных и однородных тел:
(4)
(5)

В скалярном виде для сплошных
однородных тел:
(6)

Для пластин:
h – толщина, S - площадь пластины
(7)
(8)

Для материальных линий:
а – площадь поперечного сечения
материальной линии
(9)
(10)

Методы вычисления центра тяжести:
Метод симметрии
Метод разбиения
Метод отрицательных масс

Метод симметрии
Центр масс сплошного однородного тела правильной геометрической формы находится в его геометрическом центре.
Куб
Шар

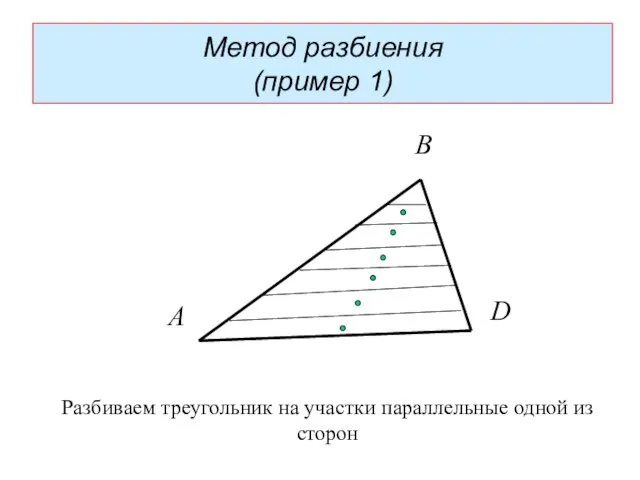
Метод разбиения
(пример 1)
А
В
D
Разбиваем треугольник на участки параллельные одной из сторон

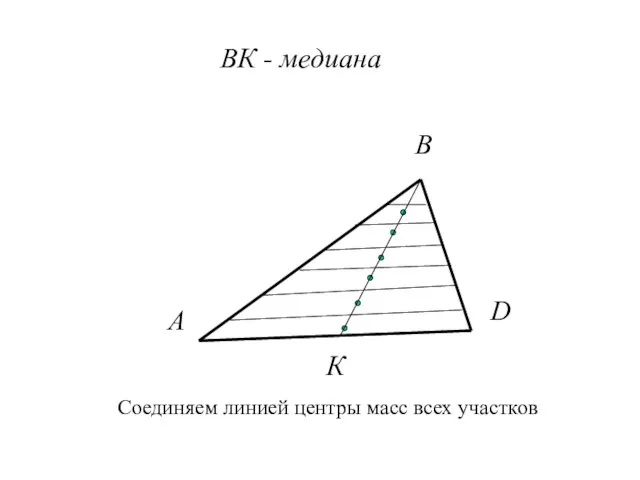
А
В
D
К
ВК - медиана
Соединяем линией центры масс всех участков

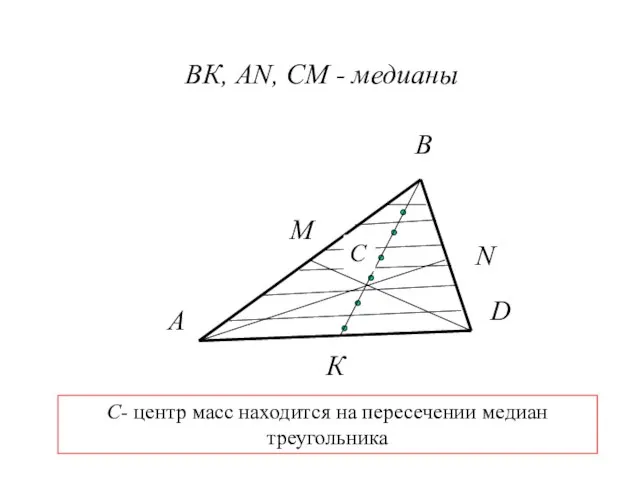
А
В
D
К
ВК, AN, CM - медианы
М
N
C
C- центр масс находится на пересечении медиан треугольника

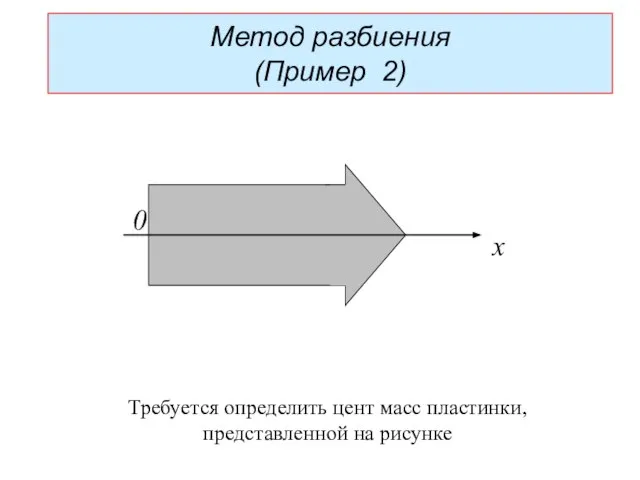
Метод разбиения
(Пример 2)
x
0
Требуется определить цент масс пластинки, представленной на рисунке

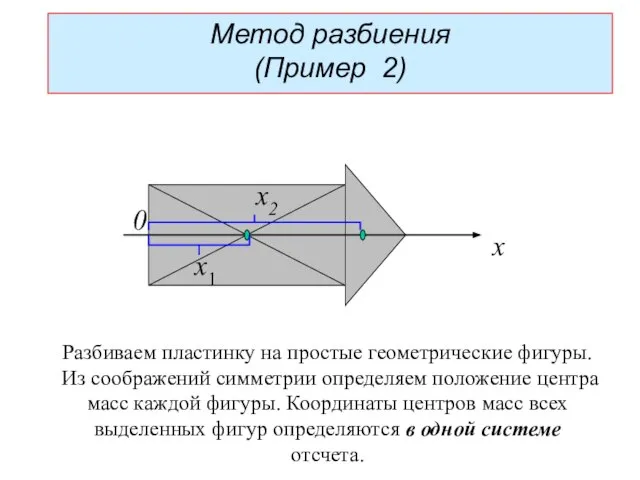
Метод разбиения
(Пример 2)
Разбиваем пластинку на простые геометрические фигуры.
Из соображений симметрии определяем положение центра масс каждой фигуры. Координаты центров масс всех выделенных фигур определяются в одной системе отсчета.
x
x1
x2
0

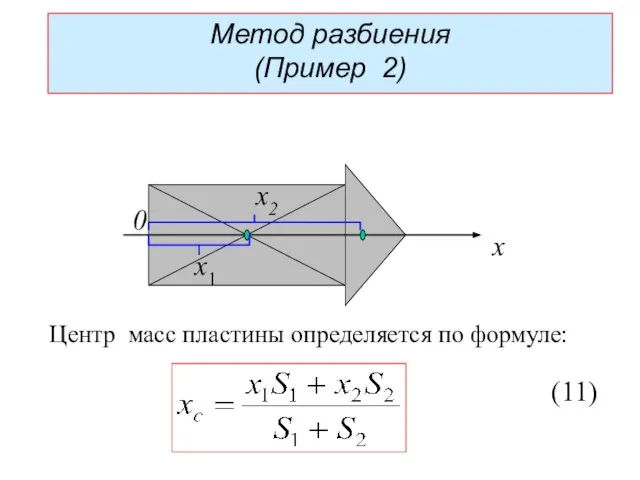
x
x1
x2
0
(11)
Метод разбиения
(Пример 2)
Центр масс пластины определяется по формуле:

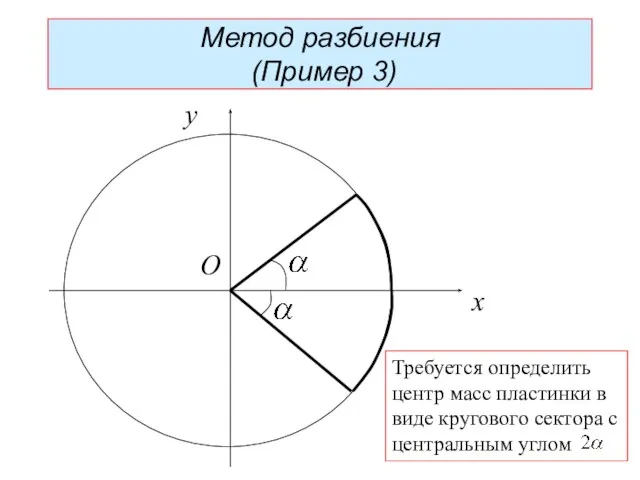
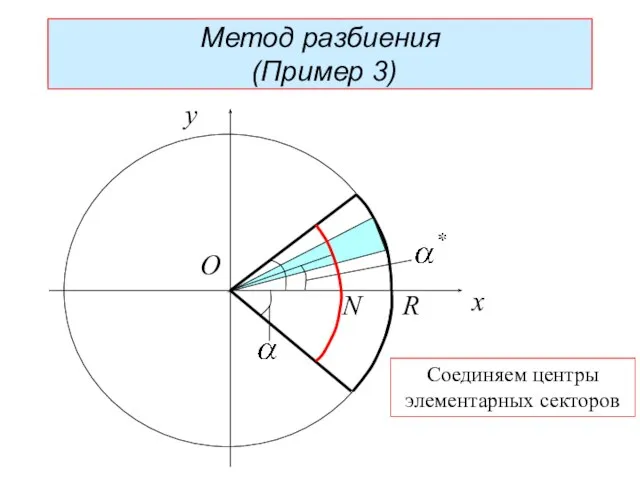
x
y
O
Метод разбиения
(Пример 3)
Требуется определить центр масс пластинки в виде кругового сектора с центральным углом

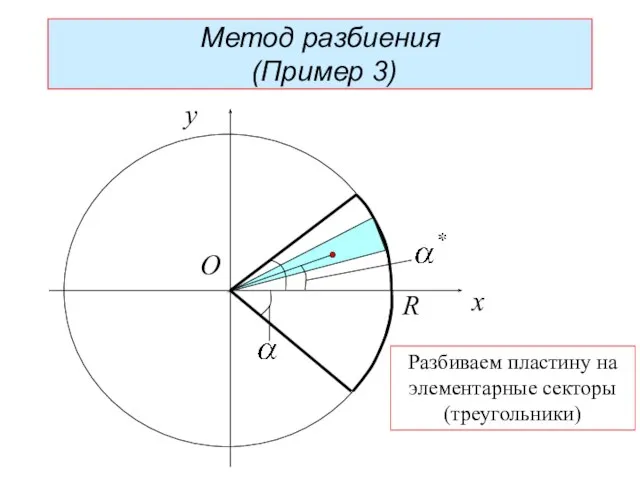
R
x
y
O
Метод разбиения
(Пример 3)
Разбиваем пластину на элементарные секторы (треугольники)

R
N
x
y
O
Метод разбиения (3)
Метод разбиения
(Пример 3)
Соединяем центры элементарных секторов

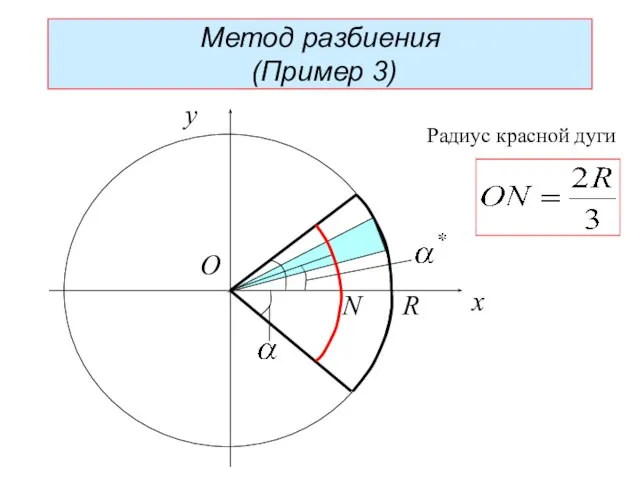
R
N
x
y
O
Радиус красной дуги
Метод разбиения
(Пример 3)

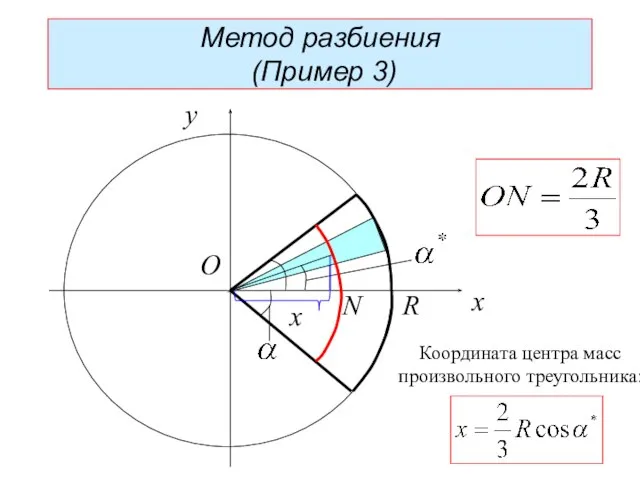
R
N
x
y
O
x
Метод разбиения
(Пример 3)
Координата центра масс
произвольного треугольника:

Длина красной дуги:

Длина красной дуги:

Так как
Длина красной дуги:

Положение центра масс кругового сектора
определяется по формуле:
(12)
Положение центра масс дуги радиуса R:
(13)

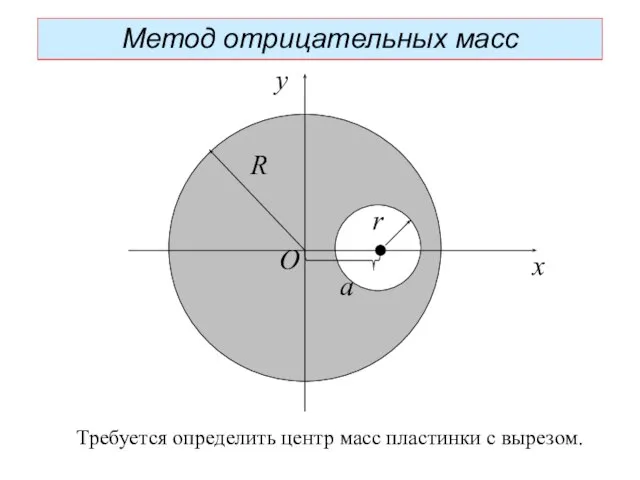
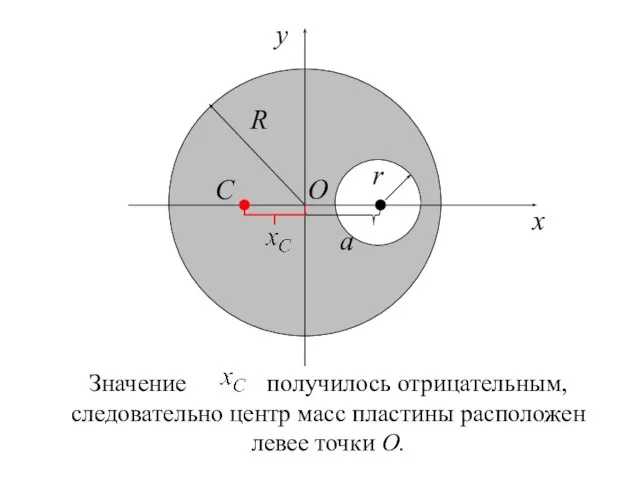
Метод отрицательных масс
R
r
a
x
y
O
Требуется определить центр масс пластинки с вырезом.

- площадь большого круга

- площадь большого круга
- площадь вырезанного круга

- площадь большого круга
- площадь вырезанного круга
координата центра масс большого
круга (без выреза)
- координата центра масс выреза

В соответствие с идеей метода площадь (масса)
выреза считается отрицательной.
Координата центра масс пластины с вырезом:
(13)
В данном случае:
(14)

R
r
a
x
O
C
y
Значение получилось отрицательным,
следовательно центр масс пластины расположен левее точки О.

КОНТРОЛЬНЫЕ ВОПРОСЫ:
Приведите пример когда положение центра
тяжести и центра масс тела не совпадают ?
2. Можно ли применить понятие «центр тяжести»
к планете?
3. Приведите пример применения метода
симметрии, не использованный в лекции.
4. Приведите пример использования метода
отрицательных масс.

ТЕСТОВЫЕ ЗАДАНИЯ
Для самоконтроля знаний рекомендуется
выполнить тестовые задания из учебного пособия:
Дробчик В.В., Шумский М.П., Дубовик В.А., Симанкин Ф.А. Теоретическая механика. (Статика). Таблица 14.