Содержание
- 2. Уравнение гармонической волны имеет вид а — амплитуда волны , ω— циклическая (круговая) частота колебаний частиц
- 3. Уравнение гармонической волны принято записывать в симметричном более удобном и простом виде. k - волновое число
- 4. Уравнение плоской волны В плоской волне волновые поверхности(где точки среды колеблются в одинаковой фазе) имеют вид
- 5. Для плоской гармонической волны и
- 6. Сферическая волна. В однородной изотропной среде продольная волна от точечного источника представляет собой сферически расходящееся возмущение
- 7. Цилиндрическая волна Цилиндрическая волна расходится от источников, равномерно распределенных вдоль оси в однородной среде. Структура цилиндрической
- 8. Волновые уравнения Для волновых процессов, существуют уравнения, являющиеся обобщенным выражением волн, независимо от их конкретного вида.
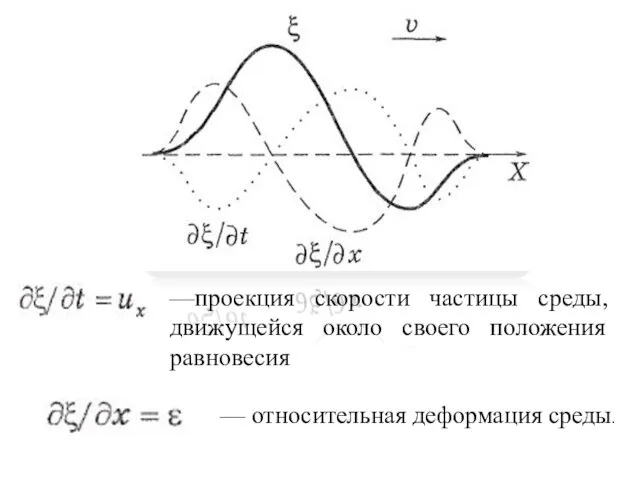
- 9. — относительная деформация среды. —проекция скорости частицы среды, движущейся около своего положения равновесия
- 10. Общее волновое уравнение Это уравнение справедливо для волны любого направления, а также и для суперпозиции таких
- 11. Это одномерное волновое уравнение 2-го порядка в частных производных. Ему удовлетворяют как возмущения вида ξ(x,t) =
- 12. Для трехмерного случая волновое уравнение имеет вид Одномерное волновое уравнение при наличии затухания γ - коэффициент
- 13. Скорость упругих волн 1.Скорость волны в тонком стержне При малых продольных деформациях стержня в стержне будет
- 14. 2.Скорость звука в жидкостях и газах скорость звуковой волны в газе − или Скорость поперечных упругих
- 15. Энергия упругой волны Плотность потенциальной энергии упругой волны Плотность полной энергии Для тонкого стержня и выражение
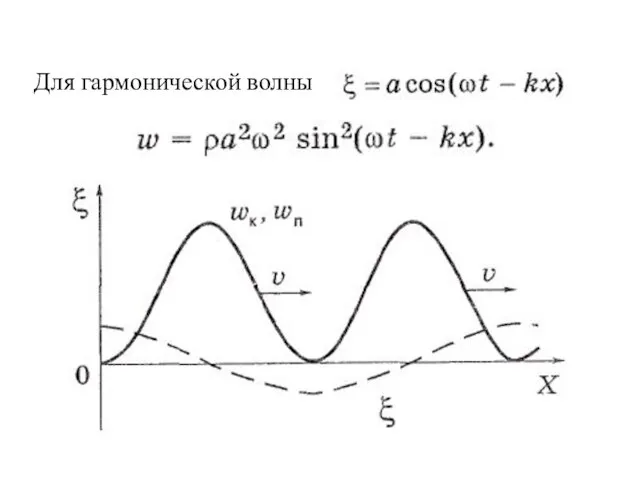
- 16. Для гармонической волны
- 17. Поток энергии −количество энергии, переносимое волной через поверхность S в единицу времени: Плотность потока энергии -
- 18. В случае монохроматической волны вектор j, как и плотность энергии, изменяется со временем по закону квадрата
- 19. формула справедлива для волн любого вида — плоской, сферической, цилиндрической, затухающих и др. Зная вектор Умова,
- 20. Для суперпозиции нескольких продольных волн вектор Умова имеет вид: — напряжение (или избыточное давление), u —
- 21. Стоячие волны При распространении в упругой среде одновременно нескольких волн возникает их наложение. Колебания частиц среды
- 22. Суперпозиция этих волн дает уравнение стоячей волны Амплитуда равна и зависит от х. ξ2 = А
- 23. В точках, для которых это максимумы амплитуды — пучности, а где — минимумы —узлы. Интервалы между
- 24. Передачи движения из одной области к другой, а значит и перетекания энергии через узлы в стоячей
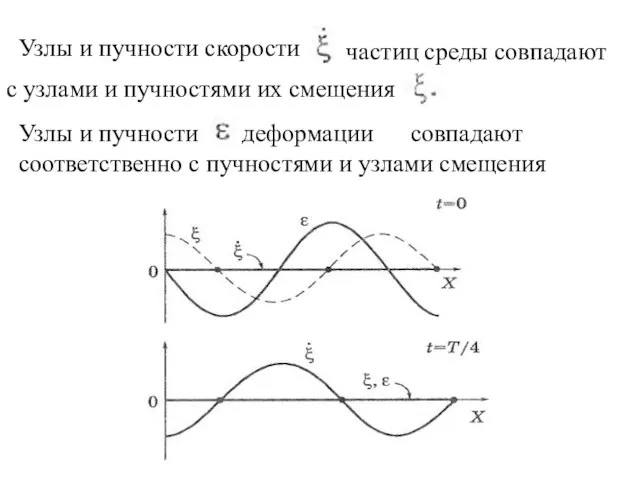
- 25. − скорости частиц - относительные деформации и - стоячие волны, причем они сдвинуты относительно друг друга
- 26. Узлы и пучности скорости частиц среды совпадают с узлами и пучностями их смещения Узлы и пучности
- 28. Скачать презентацию






















 Презентация на тему Снег
Презентация на тему Снег  Экспериментальные работы ОГЭ - 2020
Экспериментальные работы ОГЭ - 2020 Магнитное поле. Вектор магнитной индукции
Магнитное поле. Вектор магнитной индукции Закон всемирного тяготения
Закон всемирного тяготения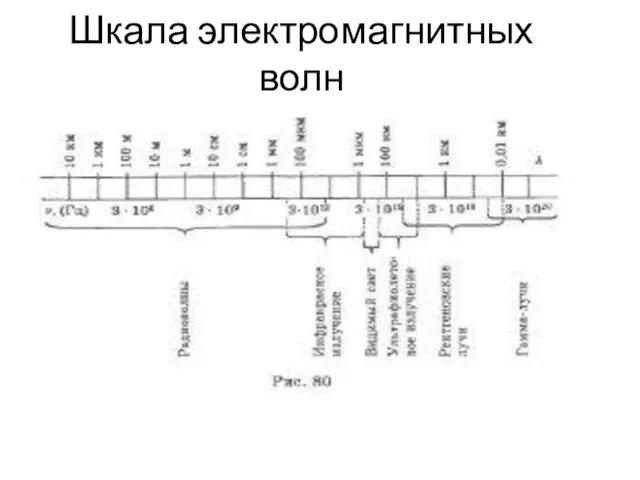 Шкала электромагнитных волн
Шкала электромагнитных волн Дифракция света. Лекции 14-15
Дифракция света. Лекции 14-15 Уравнение Клапейрона-Менделеева
Уравнение Клапейрона-Менделеева Презентация на тему Энергосберегающие лампы
Презентация на тему Энергосберегающие лампы  Физика для одноклассников
Физика для одноклассников Взаимодействие тел
Взаимодействие тел Тепловые двигатели. История создания. Устройство. Принцип действия. Коэффициент полезного действия. Применение
Тепловые двигатели. История создания. Устройство. Принцип действия. Коэффициент полезного действия. Применение Параллельная работа разных трубопроводов
Параллельная работа разных трубопроводов Барометр-анероид. Атмосферное давление на различных высотах. Физика 7 класс
Барометр-анероид. Атмосферное давление на различных высотах. Физика 7 класс Рідинні термометри
Рідинні термометри Генерирование и производство электрической энергии. Трансформатор
Генерирование и производство электрической энергии. Трансформатор Построение схемы посадки Ф45 H7/js6
Построение схемы посадки Ф45 H7/js6 Математическое моделирование физических процессов. Иллюстрационные материалы
Математическое моделирование физических процессов. Иллюстрационные материалы Расчёт режимов разомкнутых сетей
Расчёт режимов разомкнутых сетей ТОО VIVA-Мастер – авторизованный сервисный центр Pentax Medical в Казахстане
ТОО VIVA-Мастер – авторизованный сервисный центр Pentax Medical в Казахстане Регуляторы швейной машины. 6 класс
Регуляторы швейной машины. 6 класс Примеры решения задач на цепи с взаимной индукцией
Примеры решения задач на цепи с взаимной индукцией Нанотехнологии и науки о материалах
Нанотехнологии и науки о материалах Квалификационные билеты. Билет № 1
Квалификационные билеты. Билет № 1 лекция 1 (2)
лекция 1 (2) Различные изображения при помощи собирающей линзы
Различные изображения при помощи собирающей линзы Презентация на тему Вес. Невесомость. Перегрузка
Презентация на тему Вес. Невесомость. Перегрузка  Механическое движение
Механическое движение Колебания. Колебательные системы
Колебания. Колебательные системы