Вектор. Дії над векторами

Вектор – напрямлений відрізок
А
В

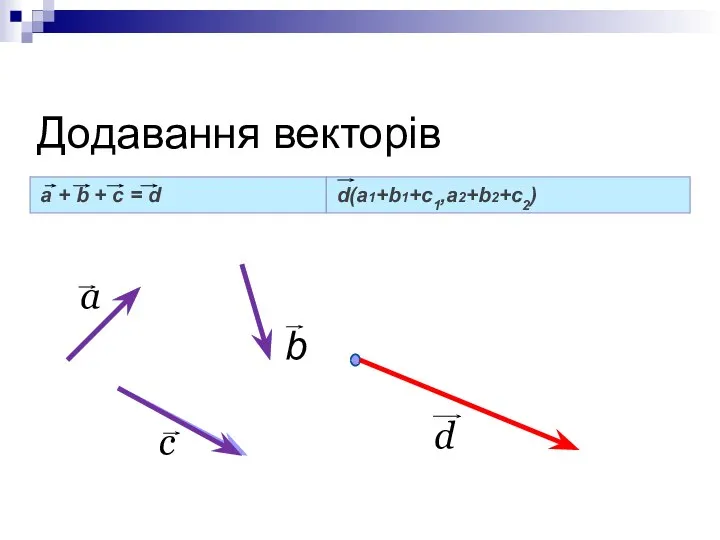
Додавання векторів
a + b + c = d
d(a1+b1+с1,a2+b2+с2)
b
a
c
d

Колінеарність векторів
Необхідною і достатньою умовою колінеарності ненульових векторів а і b є існування такого числа х, яке задовольняє рівність b = ха.
а
-а
2а
2∕3 а

Скалярний добуток векторів
Скалярним добутком векторів (а1,а2) і
(b1, b2) називається число (а1b1 + а2b2).
а × b = │а│∙ │ b│cosφ
φ
b
а

Перпендикулярність векторів
Для того, щоб два ненульових вектори були взаємно перпендикулярними, необхідно і достатньо, щоб їх скалярний добуток дорівнював 0.
а × b = 0