Волны. Волновые процессы

Волновые процессы
Колебания, возбужденные в какой-либо точке среды, распространяются в ней с конечной скоростью, зависящей от свойств среды, передаваясь от одной точки среды к другой. Дискретное (молекулярное) строение среды не учитывается и среда рассматривается как сплошная, непрерывно распределенная в пространстве и обладающая упругими свойствами.
Процесс распространения колебаний в сплошной среде называется волновым процессом или волной.
При распространении волны частицы среды не движутся вместе с волной, а колеблются около своих положений равновесия.
Вместе с волной от частицы к частице среды передаются состояние колебательного движения и его энергия.
Основным свойством всех волн, независимо от их природы, является перенос энергии без переноса вещества.

Типы волн:
волны на поверхности жидкости
упругие
электромагнитные волны.
Упругими (или механическими) волнами называются механические возмущения, распространяющиеся в упругой среде.
Упругие волны :
продольные
поперечные
В продольных волнах частицы среды колеблются в направлении распространения волны, в поперечных —в плоскостях, перпендикулярных направлению распространения волны.
Продольные волны возбуждаются в средах, в которых возникают упругие силы при деформации сжатия и растяжения (в твердых, жидких и газообразных телах).
Поперечные волны возбуждаются в среде, в которой возникают упругие силы при деформации сдвига( только в твердых телах).

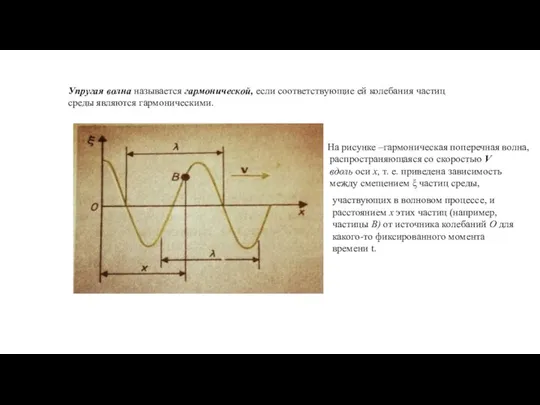
Упругая волна называется гармонической, если соответствующие ей колебания частиц среды являются гармоническими.
На рисунке –гармоническая поперечная волна,
распространяющаяся со скоростью V
вдоль оси х, т. е. приведена зависимость
между смещением ξ частиц среды,
участвующих в волновом процессе, и расстоянием х этих частиц (например, частицы В) от источника колебаний О для какого-то фиксированного момента времени t.

Геометрическое место точек, до которых доходят колебания к моменту времни t, называется волновым фронтом.
Геометрическое место точек, колеблющихся в одинаковой фазе, называется волновой поверхностью.
Волновые поверхности могут быть любой формы, в простейшем случае они представляют собой совокупность плоскостей, параллельных друг другу
(плоская волна), или совокупность концентрических сфер (сферическая волна).

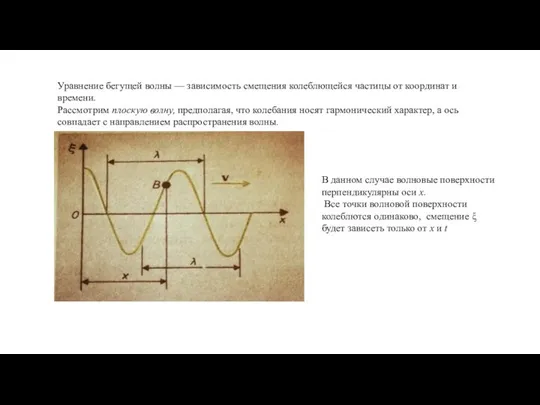
Уравнение бегущей волны — зависимость смещения колеблющейся частицы от координат и времени.
Рассмотрим плоскую волну, предполагая, что колебания носят гармонический характер, а ось совпадает с направлением распространения волны.
В данном случае волновые поверхности перпендикулярны оси х.
Все точки волновой поверхности колеблются одинаково, смещение ξ будет зависеть только от х и t

только знаком кх.

Принцип суперпозиции волн
Если среда, в которой распространяется одновременно несколько волн, линейна, т. е. ее свойства не изменяются под действием возмущений, создаваемых волной, то к ним применим принцип суперпозиции (наложения) волн:
при распространении в линейной среде нескольких волн каждая из них распространяется так, как будто другие волны отсутствуют,
результирующее смещение частицы среды в любой момент времени равно геометрической сумме смещений, которые получают частицы, участвуя в каждом из слагающих волновых процессов.
Любая волна может быть представлена в виде суммы гармонических волн, т.е. в виде волнового пакета, или группы волн.
Волновым пакетом называется суперпозиция волн, мало отличающихся друг от друга по частоте, занимающая в каждый момент времени ограниченную область пространства.

– это скорость перемещения центра группы

Максвелл еще задолго до экспериментального подтверждения существования электромагнитных волн высказал гипотезу о том, что свет – это электромагнитные волны.

Электромагнитные волны - поперечные волны:
векторы Е и Н напряженностей электрического и магнитного полей волны взаимно перпендикулярны;
лежат в плоскости, перпендикулярной вектору v скорости рас­пространения волны,
векторы Е, Н и v образуют правовинтовую систему.
В электромагнитной волне векторы Е и Н все­гда колеблются в одинаковых фазах
– одновременно обращаются в нуль и одновременно достигают максимальных значений.

Синусоидальная электромагнитная волна называется монохроматической волной.
В каждой точке электромагнитного поля монохроматической волны проекции векторов
E и H на оси координат инерциальной системы отсчета
совершают гармонические колебания одинаковой частоты ν, называемой частотой волны.

Вектора напряженностей электрического и магнитного полей плоской линейно поляризованной монохроматической волны в различных точках луча (ОХ) в один и тот же момент времени. Оси OY и OZ проведены в направлениях колебания векторов E и H.
Плоскость, проходящая через электрический вектор E и луч (OX) называется плоскостью поляризации линейно поляризованной волны.