Задача о движении внешней нагрузки по битому льду в канале

/18
План
Мотивация.
Постановка задачи.
Единственность классического решения.
Поведение прогибов битого льда при больших временах.
Заключение.

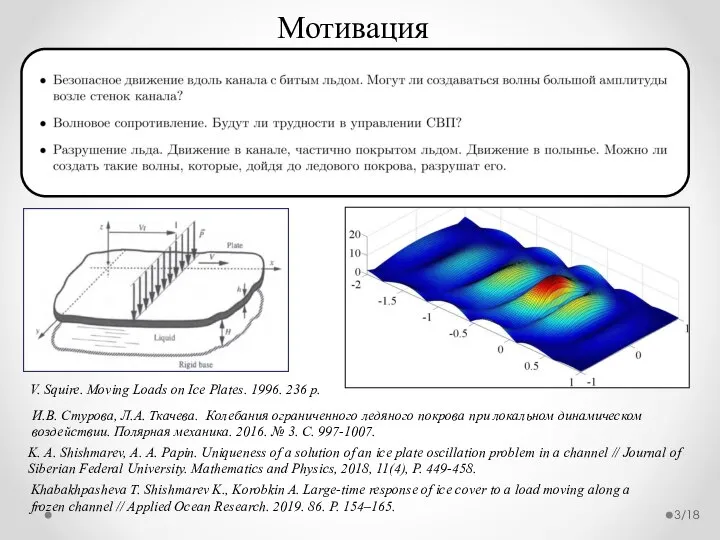
/18
Мотивация
И.В. Стурова, Л.А. Ткачева. Колебания ограниченного ледяного покрова при локальном динамическом воздействии. Полярная механика. 2016. № 3. С. 997-1007.
Khabakhpasheva T. Shishmarev K., Korobkin A. Large-time response of ice cover to a load moving along a frozen channel // Applied Ocean Research. 2019. 86. P. 154–165.
V. Squire. Moving Loads on Ice Plates. 1996. 236 p.
K. A. Shishmarev, A. A. Papin. Uniqueness of a solution of an ice plate oscillation problem in a channel // Journal of Siberian Federal University. Mathematics and Physics, 2018, 11(4), P. 449-458.

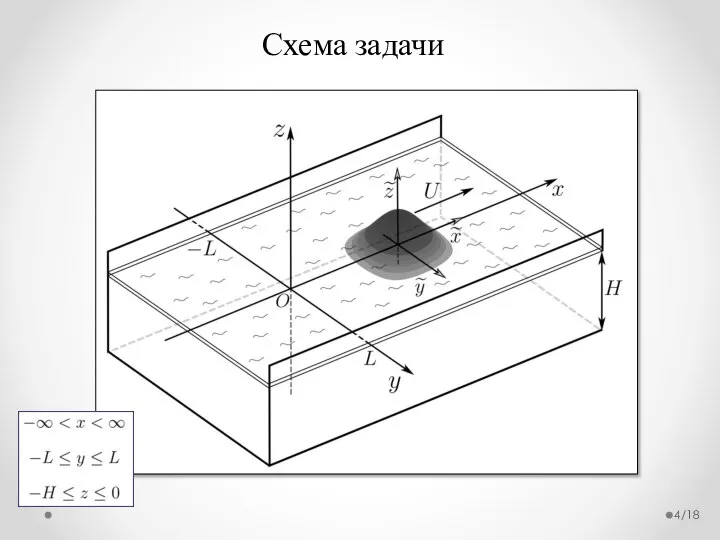
Схема задачи
/18

Постановка задачи
/18

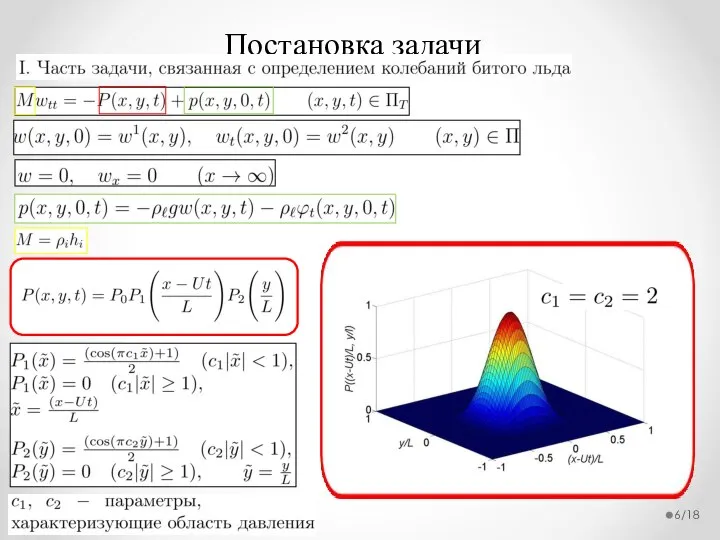
/18
Постановка задачи

Единственность классического решения
/18

Единственность классического решения
/18

/18
Метод решения. Преобразование Фурье вдоль канала

/18
Метод решения. Метод разделения переменных

/18

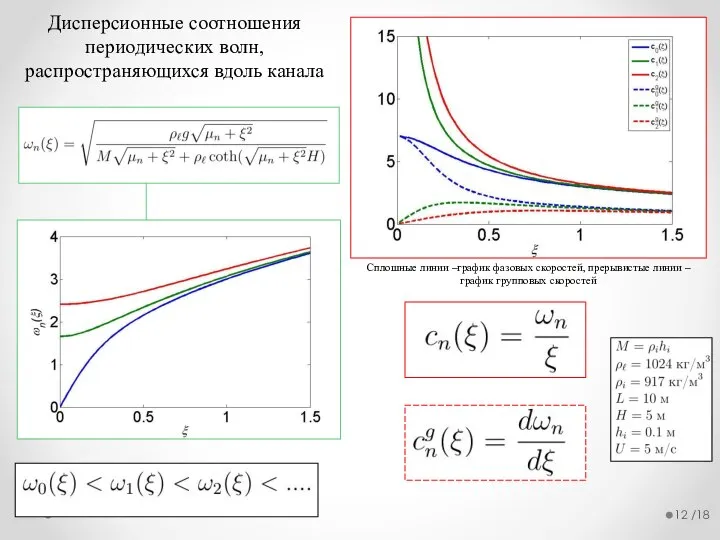
/18
Дисперсионные соотношения периодических волн, распространяющихся вдоль канала
Сплошные линии –график фазовых скоростей, прерывистые линии – график групповых скоростей

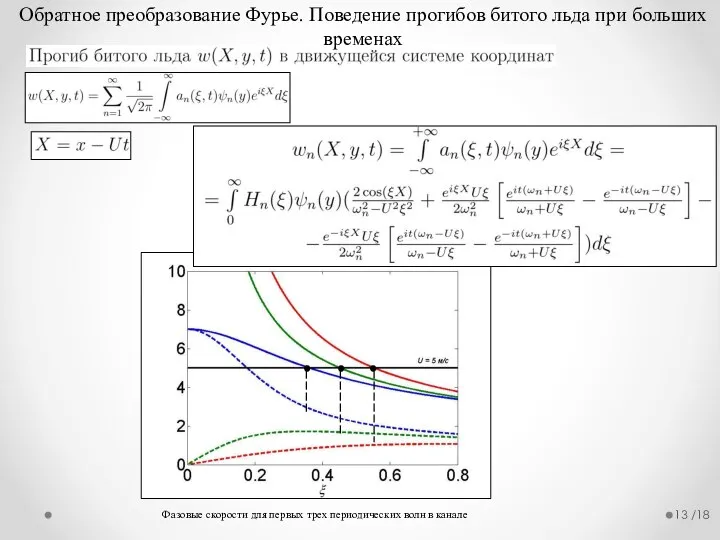
/18
Обратное преобразование Фурье. Поведение прогибов битого льда при больших временах
Фазовые скорости для первых трех периодических волн в канале

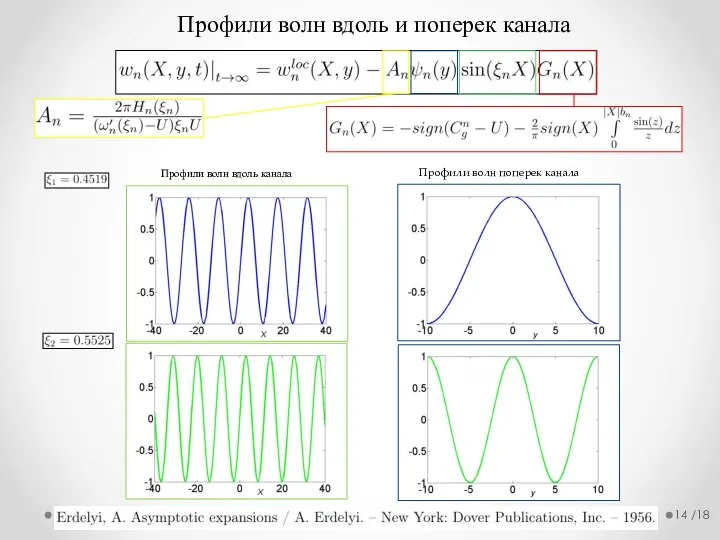
/18
Профили волн вдоль и поперек канала
Профили волн вдоль канала
Профили волн поперек канала

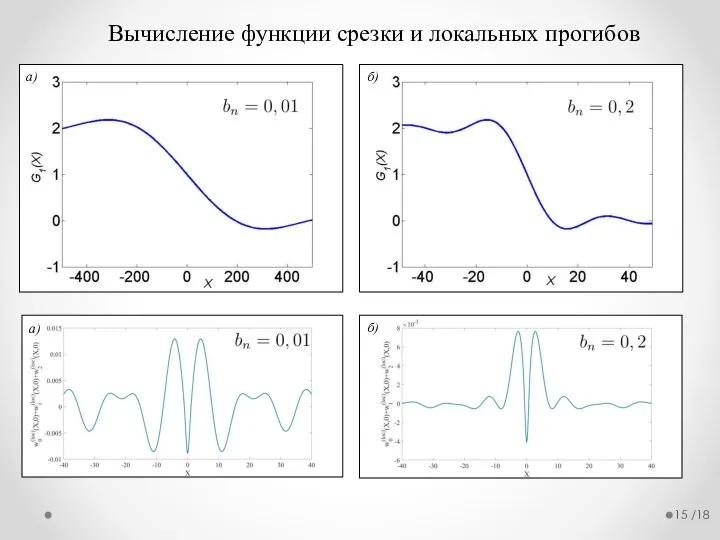
/18
Вычисление функции срезки и локальных прогибов
а)
б)
а)
б)

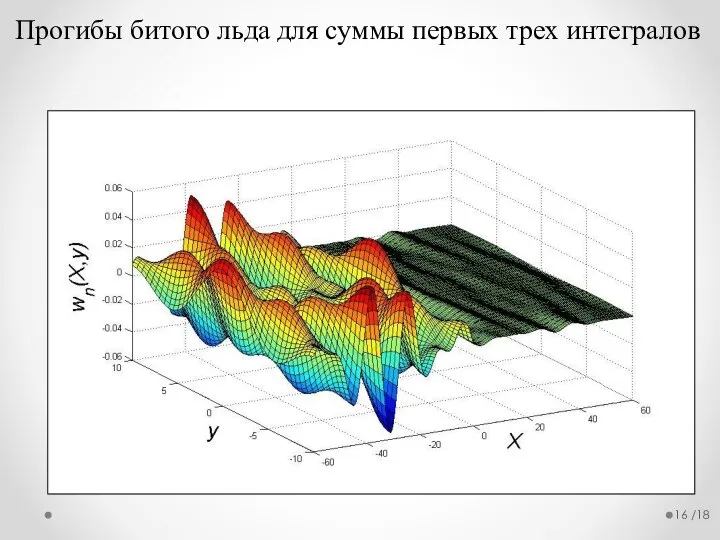
/18
Прогибы битого льда для суммы первых трех интегралов

/18
Заключение
Рассмотрена нестационарная задача для определения прогибов битого льда в канале под действием внешней нагрузки, движущейся с постоянной скоростью вдоль центральной линии канала. Доказана теорема единственности классического решения рассматриваемой задачи. Исследовано поведение колебаний битого льда в канале под действием внешней нагрузки при больших временах. Решение получено в виде формулы, дающей простую интерпретацию для анализа формы колебаний битого льда. Получено, что при больших временах колебания битого льда состоят из волн, распространяющихся сзади нагрузки, таких волн в канале будет счетное число, и из локальных прогибов в области нагрузки, которые затухают при отдалении от нагрузки.
Автор принимал активное участие в получении результатов: постановке задачи, численном и аналитическом исследовании, анализе и обсуждении полученных результатов, а также в оформлении результатов в виде публикаций и научных докладов.