8-2a_КодированиеВведение

Кодирование информации
§ 4. Язык – средство кодирования

Определения
Кодирование — это представление информации в форме, пригодной для её хранения, передачи и автоматической обработки.
Код — это правило, по которому сообщение преобразуется в цепочку знаков.
Язык — это система знаков и правил, используемая для записи и передачи информации.
Естественные языки – сформировались в результате развития общества.

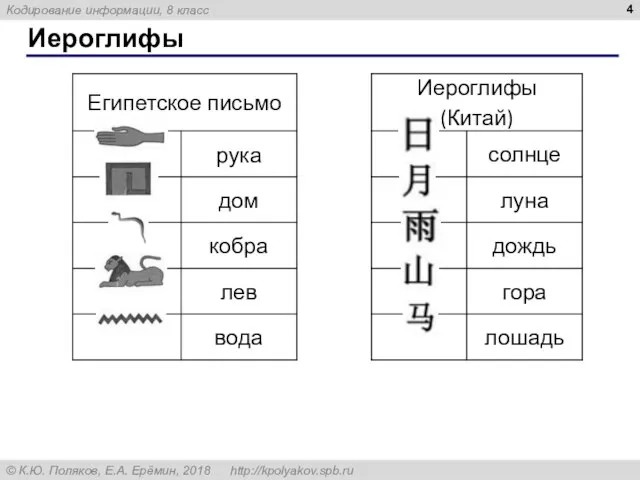
Иероглифы

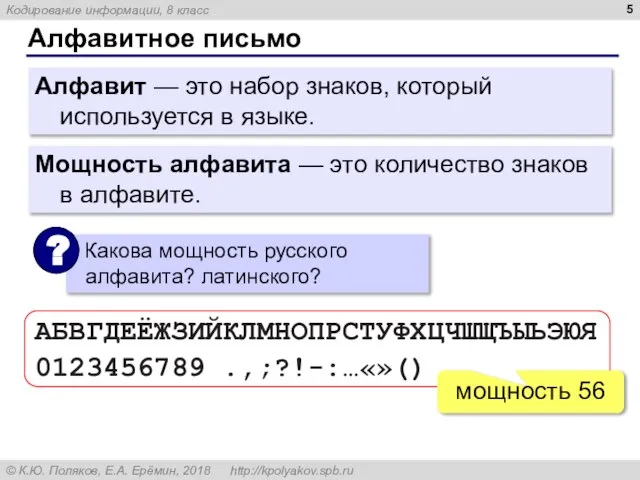
Алфавитное письмо
АБВГДЕЁЖЗИЙКЛМНОПРСТУФХЦЧШЩЪЫЬЭЮЯ
0123456789 .,;?!-:…«»()
мощность 56
Алфавит — это набор знаков, который используется в языке.
Мощность алфавита — это количество знаков в алфавите.

Какие бывают языки?
1. e2-e4 e7-e5…
Формальный язык – это язык, в котором однозначно определяется значение каждого слова, а также правила построения предложений и придания им смысла.

Сообщения
Пример: алфавит {0, 1}.
Сообщения длины 2:
00 01 10 11
всего 4
Сообщение — это любая последовательность символов некоторого алфавита.
Комбинаторика — это наука, изучающая комбинации объектов.

Сообщения
Пример: алфавит {@, #, $, %}.
Сообщения длины 1: @ # $ %.
Сообщения длины 2:
@@ @# @$ @%
#@ ## #$ #%
$@ $# $$ $%
%@ %# %$ %%
всего 16
всего 4

Количество возможных сообщений
Если алфавит языка состоит из M символов (имеет мощность M), количество различных сообщений длиной L знаков равно
N = M L
Сколько
возможных 5-буквеных слов в русском языке?
возможных 3-буквеных слов в английском языке?
возможных сообщений длиной L символов в алфавите {+, –}?
335
263
2L

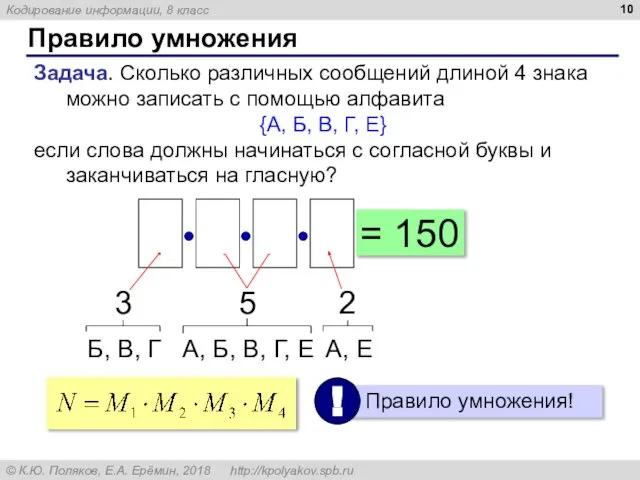
Правило умножения
Задача. Сколько различных сообщений длиной 4 знака можно записать с помощью алфавита
{А, Б, В, Г, Е}
если слова должны начинаться с согласной буквы и заканчиваться на гласную?
А, Б, В, Г, Е
5
3
Б, В, Г
2
А, Е

Правило умножения
Задача. Сколько существует четырёхзначных чисел, составленных из чётных цифр, в которых цифры не повторяются?
0, 2, 4, 6, 8
5
4
2, 4, 6, 8
одна цифра уже использована!

Правило сложения
Задача. Сколько сообщений длиной от 2 до 5 символов можно записать с помощью алфавита {0, 1}?
L = 2: N2 = 22 = 4
L = 3: N3 = 23 = 8
L = 4: N4 = 24 = 16
L = 5: N5 = 25 = 32

Генетический код
Типы звеньев (нуклеотиды)
A – аденин (Adenine)
C – цитозин (Cytosine) G – гуанин (Guanine)
T – тимин (Thymine)
M = 4
3% – гены (информация о белкáх)
Белки ← 20 типов аминокислот
L = 3
42 < 20 < 43

Интеллект-карта

Кодирование информации
§ 5. Дискретное кодирование

Дискретизация
Дискретизация — это представление единого объекта в виде множества отдельных элементов.
t = 18°C

Хранение данных в компьютере
Компьютер — это дискретное устройство.
Двоичный код – это код, в котором используются два знака (0 и 1). Все данные в компьютере хранятся в двоичном коде.
Бит – это одна двоичная цифра (0 или 1).
010010

Двоичное кодирование
Кодовая таблица
ГАГАРА:
010 000 010 000 100 000
Равномерный код — это код, в котором все кодовые слова имеют одинаковую длину.
2L

Декодирование
Кодовая таблица
Р А Г Р А
100000010100000
?:
Декодирование — это восстановление исходного сообщения из кода.
5
100 000 010 100 000
по 3

Как выбрать длину кодовых слов?
Задача. В сообщении встречаются 25 символов. Выберите минимальную длину кодовых слов, при которой все они могут получить разные коды.
1 бит:
2 варианта
2 бита:
4 варианта
3 бита:
8 вариантов
4 бита:
16 вариантов
5 битов:
< 25
< 25
< 25
< 25
Выбор длины кодовых слов L: ML ≥ M0, где M0 — мощность алфавита исходного сообщения и M — мощность нового алфавита.
2L ≥ 25

Неравномерные коды
Недостаток равномерных кодов – длинные закодированные сообщения.
Идея: часто встречающиеся символы должны иметь более короткие коды!

Неравномерные коды
Кодовая таблица
ГАГАРА:
1 0 1 0 10 0
Неравномерный код — это код, в котором кодовые слова имеют разную длину.
Декодирование: 010010

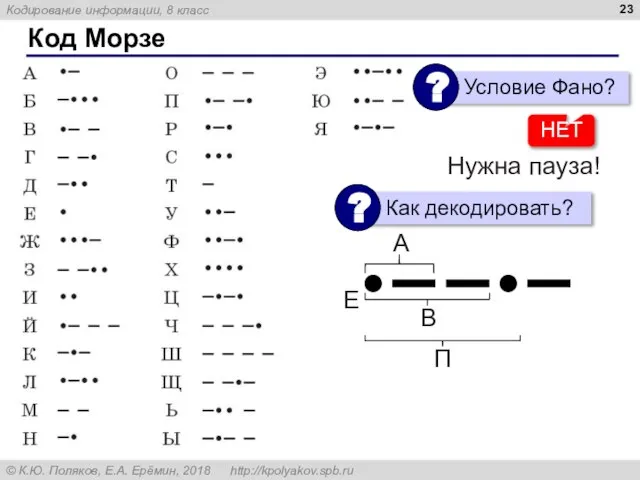
Код Морзе
НЕТ
Нужна пауза!
Е

Неравномерные коды
Кодовая таблица
Декодирование: 01001011
АГАГР
Неравномерный код декодируется однозначно, если выполняется условие Фано: ни одно кодовое слово не совпадает с началом
другого кодового слова.

Как измерить информацию?
Количество информации в битах определяется длиной сообщения в двоичном коде.
10101100
8 битов

Единицы измерения
1 байт = 8 бит
1 Кбайт (килобайт) = 1024 байта
1 Мбайт (мегабайт) = 1024 Кбайт
1 Гбайт (гигабайт) = 1024 Мбайт
1 Тбайт (терабайт) = 1024 Гбайт
210
1 байт = 23 бит
1 Кбайт = 210 байта = 210 ⋅ 23 бит = 213 бит
1 Мбайт = 210 Кбайт = 210 ⋅ 213 бит = 223 бит

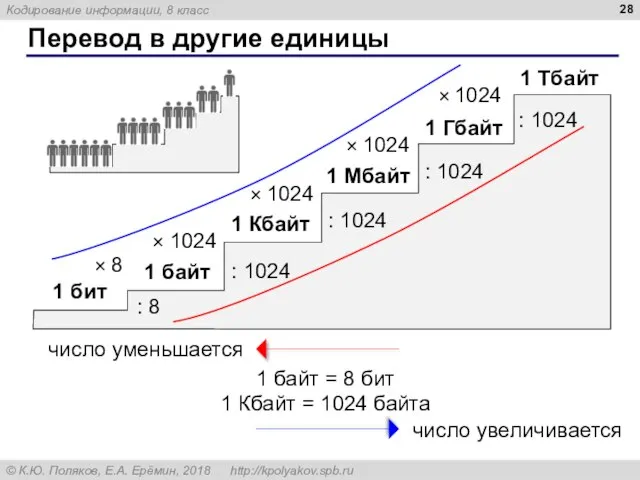
Перевод в другие единицы
2 Кбайт = 2 × (1 Кбайт) = 2 × 1024 байт
= 2048 байт
= 2048 × (1 байт) = 2048 × 8 бит
= 16 384 бита
Через степени числа 2:
2 Кбайт = 2 × 210 байт = 211 байт
= 211 × 23 бит = 214 бит.

Перевод в другие единицы
: 8
: 1024
: 1024
: 1024
: 1024
× 1024
× 1024
× 1024
× 1024
× 8
1 байт = 8 бит
1 Кбайт = 1024 байта
число уменьшается
число увеличивается

Алфавитный подход
Задача 1. Алфавит русского языка содержит 33 символа. Определите наименьшую длину кодовых слов при кодировании сообщений на русском языке с помощью равномерного кода.
M = 33
i = ?
25 < 33 ≤ 26
i бит → 2i разных кодов
5 бит на символ не хватает…
6 бит на символ хватает!
Ответ: i = 6 бит
i = 7 бит
M ≤ 2i

Алфавитный подход
Задача 2. Текст длиной 160 символов записан с помощью алфавита из 26 символов. Определите количество информации в сообщении, закодированном с помощью равномерного кода наименьшей длины.
L = 160
I = ?
M = 26
I = L · i
бит на символ
24 < 26 ≤ 25
5 бит на символ хватает!
i = 5
Ответ: I = 800 бит = 100 байт

Алфавитный подход
Задача 3. Пароль длиной 8 символов может содержать английские буквы (заглавные и строчные), цифры и специальные знаки: @, #, $, %. Сколько бит памяти нужно выделить для хранения пароля?
L = 8
I = ?
M = 26·2+10 + 4 = 66
I = L · i
26 < 66 ≤ 27
7 бит на символ хватает!
i = 7
Ответ: I = 56 бит = 7 байт

Алфавитный подход
Задача 4. Текст длиной 4096 символов занимает в памяти 4 Кбайта. Определите наибольшее возможное количество символов в алфавите.
L = 4096
I = 4 Кбайт
M = ?
M ≤ 28 = 256
Ответ: M = 256
i бит → 2i разных кодов
M ≤ 2i
I = L · i
i = I : L
i = 4 : 4096

Алфавитный подход
Задача 5. Участники соревнований по бегу получили номера от 1 до 100. На финише автоматическое устройство записывает номер спортсмена. Сколько байт нужно для хранения номеров 80 спортсменов?
M = 100
L = 80
I = ?
i бит → 2i разных кодов
M ≤ 2i
I = L · i
26 < 100 ≤ 27
7 бит на символ хватает!
Ответ: I = 70 байт

Кодирование информации
§ 7. Кодирование с обнаружением ошибок

Обнаружение ошибок
Бит чётности:
00 01 10 11
⇒ 000 011 101 110
Если в принятом блоке нечётное число «1» – ошибка!
принято: 010 110 000 111 000
Для файлов – контрольные суммы (хэш):
CRC = Cyclic Redundancy Code
MD5, SHA-1
10010

Обнаружение ошибок
Получено (с битами чётности):
101111000100011000
Разбиваем на группы по 3 бита:
101 111 000 100 011 000
Помечаем блоки с ошибками:
101 * 000 * 011 000
Убираем бит чётности в каждом блоке (последний):
10 * 00 * 01 00
Декодируем по таблице:
Р * К * А К
к коду каждой буквы справа добавляется бит чётности

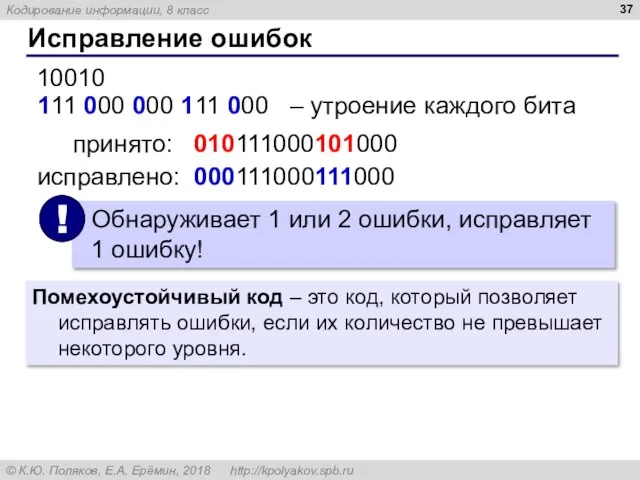
Исправление ошибок
111 000 000 111 000 – утроение каждого бита
принято: 010111000101000
исправлено: 000111000111000
10010
Помехоустойчивый код – это код, который позволяет исправлять ошибки, если их количество не превышает некоторого уровня.

Исправление ошибок
10011 11100 00000

Исправление ошибок
10101 11001 01001

Конец фильма
ПОЛЯКОВ Константин Юрьевич
д.т.н., учитель информатики
ГБОУ СОШ № 163, г. Санкт-Петербург
[email protected]
ЕРЕМИН Евгений Александрович
к.ф.-м.н., доцент кафедры мультимедийной дидактики и ИТО ПГГПУ, г. Пермь
[email protected]