Рекуррентная сеть Хопфилда

Рекуррентная сеть Хопфилда представляется в виде системы с обратной связью выхода сети с ее входом. Выходные сигналы нейронов являются одновременно входными сигналами сети. В классической сети Хопфилда отсутствует связь выхода нейрона с собственным входом, что соответствует значению веса 0 на главной диагонали матрицы, а матрица весов является симметричной.

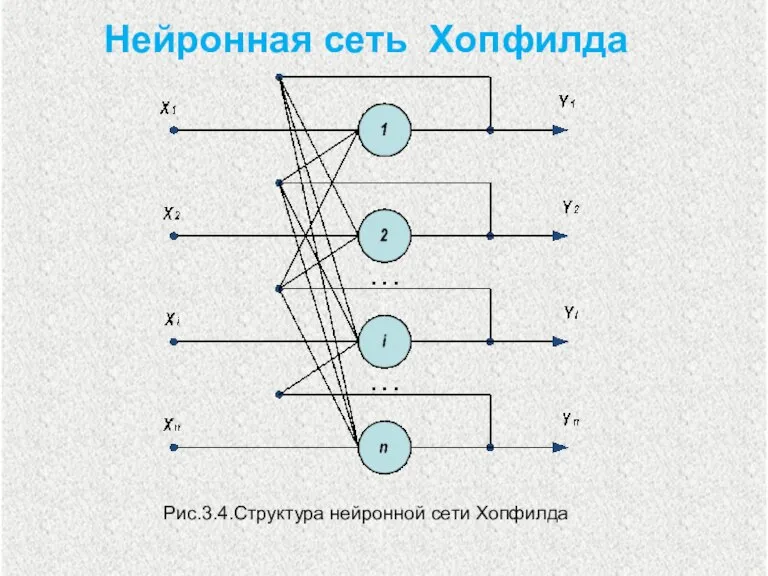
Нейронная сеть Хопфилда
Рис.3.4.Структура нейронной сети Хопфилда

Входной сигнал - вектор X={xi: i=1,...,n}, n – число нейронов в сети и размерность входных и выходных векторов.
Каждый элемент xi равен +1, или -1.
Вектор k-го примера - Xk, а его компоненты - xik, k=1,...,m, m – число примеров.
Если образ распознан, выход сети равен Y=Xk,
где Y – вектор выходных значений сети: Y={yi, i=1,...,n}.
Инициализация сети
ВЕСА СЕТИ
где i и j – индексы соответственно предсинаптического и постсинаптического
нейронов;
xik, xjk – i-ий та j-ый элементы вектора k-го примера.
Рекуррентные сети устойчивы, если весовая матрица W = (wij)
симметрична, а на ее главной диагонали – нули:
1) wij = wji для всех i ¹ j ; (2.58)
2) wii = 0 для всех i .

В качестве входных данных сети Хопфилда можно использовать двоичные значения. Здесь мы будем использовать +1 для обозначения состояния «включено» и
(-1) для состояния «выключено».
Расчет суммарного сигнала netj нейрона Sj вычисляется по формуле:
где Si – обозначает состояние нейрона с номером i.

Когда элемент обновляется, его состояние изменяется в соответствии с правилом:
Эта зависимость называется сигнум - функцией и записывается следующим образом:
Если комбинированный ввод равен 0, то элемент остается в состоянии, в котором он был до обновления.

Сеть Хопфилда ведет себя как память и процедура сохранения отдельного вектора (образца) представляет собой вычисление прямого произведения вектора с ним самим. В результате этой процедуры создается матрица, задающая весовые значения сети Хопфилда, в которой все диагональные элементы должны быть установлены равными 0 (поскольку диагональные элементы задают автосвязи элементов, а элементы сами с собой не связаны).
Таким образом, весовая матрица, соответствующая сохранению вектора X, задается следующей формулой:

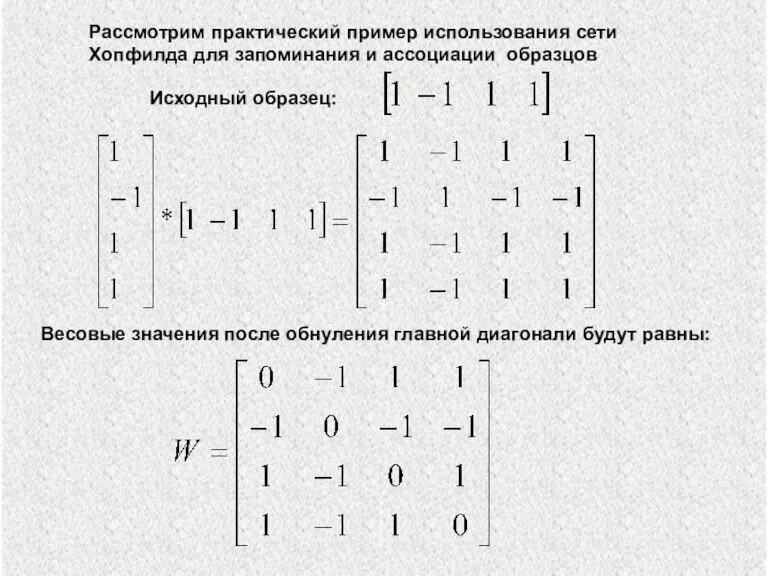
Весовые значения после обнуления главной диагонали будут равны:
Исходный образец:
Рассмотрим практический пример использования сети Хопфилда для запоминания и ассоциации образцов

Отметим, что первый элемент вектора [1 -1 1 1] остался в том же состоянии (1)
АНАЛОГИЧНО РАССЧИТЫВАЮТСЯ СОСТОЯНИЯ ОСТАВШИХСЯ ЭЛЕМЕНТОВ: -1 1 1
Первый элемент обновляется путем умножения образца на первый столбец матрицы весов

Элементы должны обновляться в случайном порядке. Для иллюстрации будем обновлять элементы в порядке 3, 4, 2, 1. Сначала рассмотрим элемент 3-ий:
Проверим устойчивое состояние сети Хопфилда для найденных весов W, но для искаженного образца:
Элемент 3-ий не поменял своего значения (1).

Элемент 4-ый остается в том же состоянии (1).
Теперь рассмотрим элемент 1-ый:
Рассмотрим состояние для элемента 4-го:
Следует отметить, что 1-ый элемент изменил свое состояние с -1 на 1.

Элемент 2-ой остается в том же состоянии (-1).
Следует отметить, что мы выявили исходный вектор (1 -1 1 1), характеризующий устойчивое состояние сети
Рассмотрим состояние для элемента 2-го:

При запоминании двух и более образцов используем процедуру сложения полученных матриц. В результирующей матрице обязательно обнуляем главную диагональ
Определим весовую матрицу сети Хопфилда для двух образцов: