Графический метод решения задач линейного программирования. Тема 4

1 ЭТАП. НАХОЖДЕНИЕ ОДР
Условие задачи:
Выписываем только ограничения и приравниваем левую их часть к правой

(0;10)
(0;3)
(0;-4)
(0;10)
1) Теперь находим по две точки для каждого уравнения. Для этого поочередно приравниваем по одному неизвестному к нулю;
(3;0)
(-3;0)
(4;0)
(10;0)
2) Затем пронумеруем каждую прямую;
I
II
III
IV
3) И теперь смело переходим к координатной плоскости;

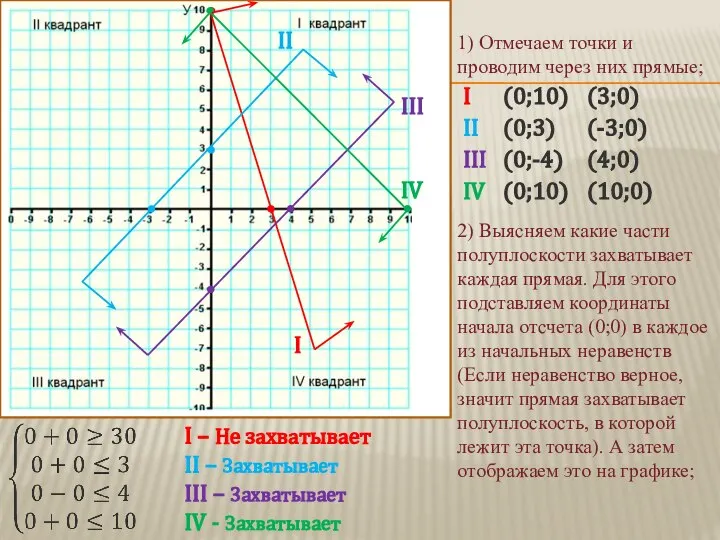
I
II
III
IV
(0;10)
(0;3)
(0;-4)
(0;10)
(3;0)
(-3;0)
(4;0)
(10;0)
1) Отмечаем точки и проводим через них прямые;
I
II
III
IV
2) Выясняем какие части полуплоскости захватывает каждая прямая. Для этого подставляем координаты начала отсчета (0;0) в каждое из начальных неравенств (Если неравенство верное, значит прямая захватывает полуплоскость, в которой лежит эта точка). А затем отображаем это на графике;
I – Не захватывает
II – Захватывает
III – 3ахватывает
IV - Захватывает

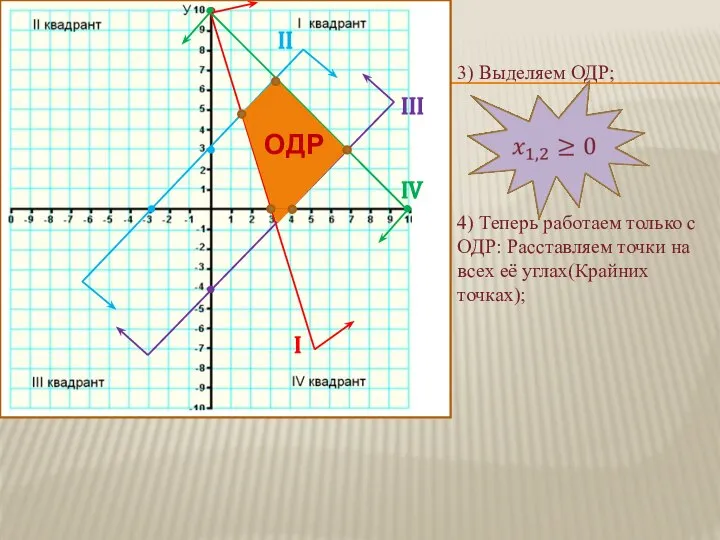
I
II
III
IV
ОДР
4) Теперь работаем только с ОДР: Расставляем точки на всех её углах(Крайних точках);
3) Выделяем ОДР;

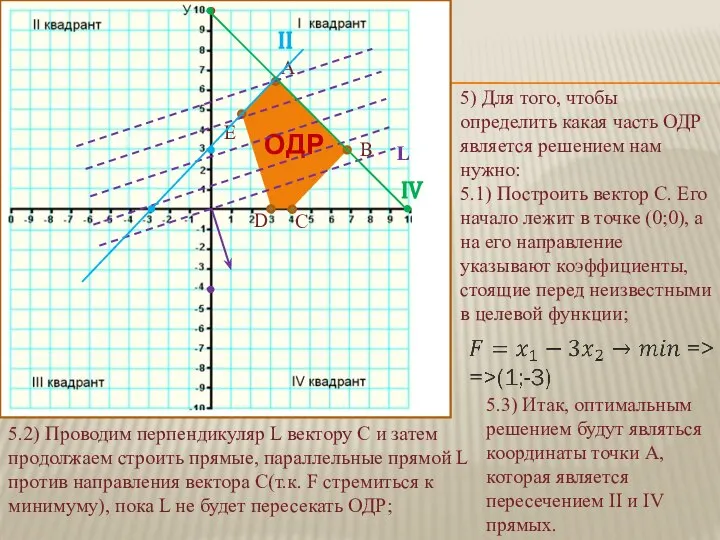
ОДР
А
Е
В
С
D
5) Для того, чтобы определить какая часть ОДР является решением нам нужно:
5.1) Построить вектор C. Его начало лежит в точке (0;0), а на его направление указывают коэффициенты, стоящие перед неизвестными в целевой функции;
5.2) Проводим перпендикуляр L вектору C и затем продолжаем строить прямые, параллельные прямой L против направления вектора С(т.к. F стремиться к минимуму), пока L не будет пересекать ОДР;
L
5.3) Итак, оптимальным решением будут являться координаты точки А, которая является пересечением II и IV прямых.
II
IV