Содержание
- 2. Логика Способность к развитому абстрактному мышлению, которая, формируется логикой, и есть то, что отделяет нас от
- 3. Логика Клод Шеннон (1916-2001). Его исследования позволили применить алгебру логики в вычислительной технике Аристотель (384-322 до
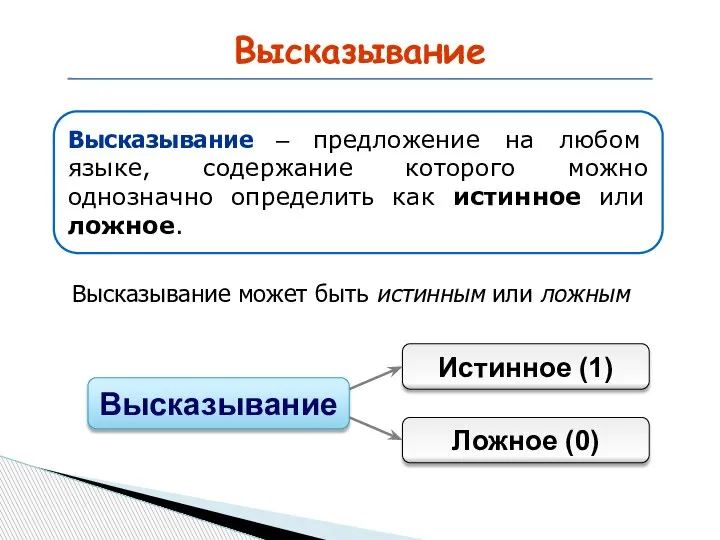
- 4. Высказывание Высказывание может быть истинным или ложным Высказывание Истинное (1) Ложное (0) Высказывание – предложение на
- 5. Высказывание В русском языке высказывания выражаются повествовательными предложениями: Земля вращается вокруг Солнца. Москва - столица. Но
- 6. Примеры высказываний Москва больше Санкт-Петербурга Все мальчики любят играть в футбол “Лед - твердое состояние воды”
- 7. Высказывание Объясните, почему следующие предложения не являются высказываниями. 1) Какого цвета этот дом? 2) Число Х
- 8. Высказывание или нет Зимой идет дождь. Снегири живут в Крыму. Кто к нам пришел? У треугольника
- 9. Алгебра логики Алгебра логики возникла в середине XIX века в трудах английского математика Джорджа Буля. Ее
- 10. Алгебра логики Алгебра логики позволяет определять истинность или ложность составных высказываний, не вникая в их содержание.
- 11. Простые и сложные высказывания Высказывания могут быть простыми или сложными. Сложные высказывания состоят из простых высказываний,
- 12. В следующих высказываниях выделите простые высказывания, обозначив каждое из них буквой. Запишите с помощью букв и
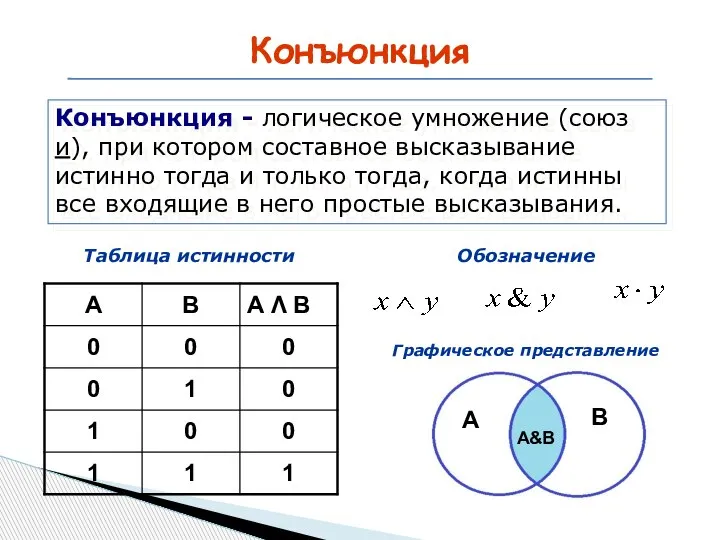
- 13. Конъюнкция Конъюнкция - логическое умножение (союз и), при котором составное высказывание истинно тогда и только тогда,
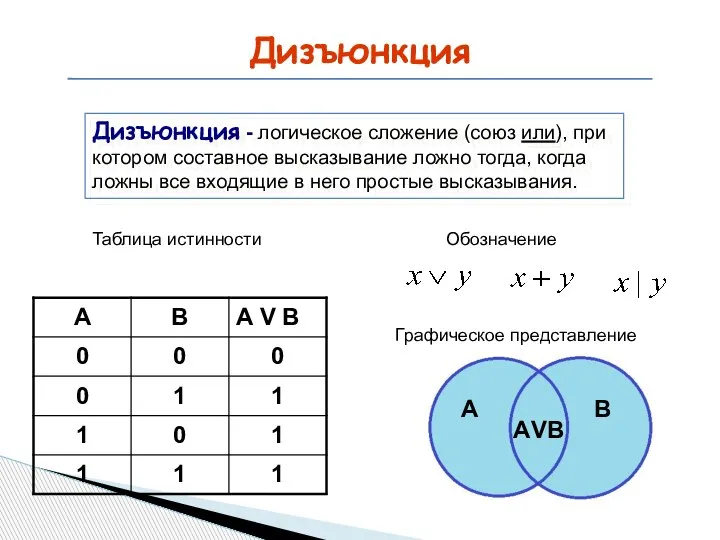
- 14. Дизъюнкция Дизъюнкция - логическое сложение (союз или), при котором составное высказывание ложно тогда, когда ложны все
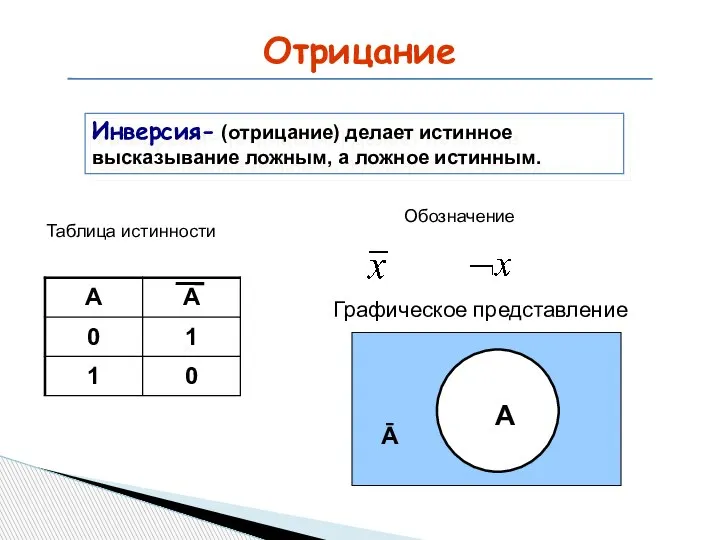
- 15. Отрицание Инверсия- (отрицание) делает истинное высказывание ложным, а ложное истинным. Таблица истинности Обозначение Графическое представление A
- 16. Импликация Импликация - (логическое следование - если…, то…). Ложно тогда и только тогда, когда из истинного
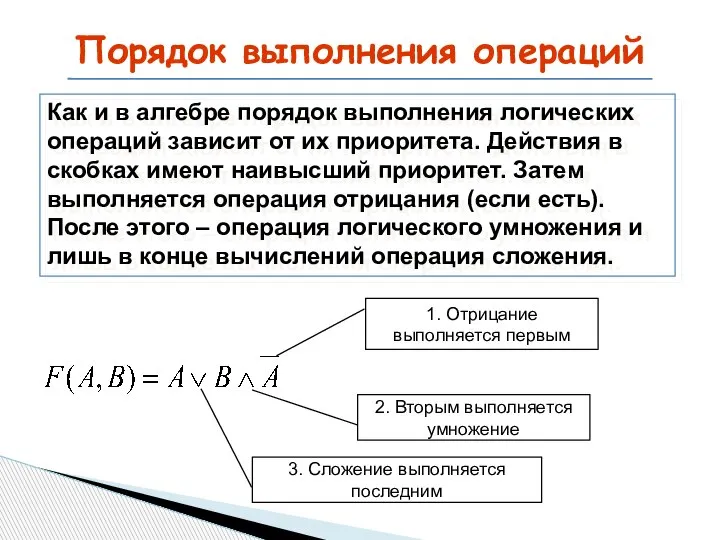
- 17. Порядок выполнения операций Как и в алгебре порядок выполнения логических операций зависит от их приоритета. Действия
- 18. Импликация Преобразования по закону де Моргана
- 19. Даны два простых высказывания: А = {2 • 2 = 4}, В = {2 • 2
- 20. Задания А = «Сейчас нет дождя» В = «Форточка закрыта» Составить сложные высказывания A Λ B
- 21. Построение таблиц истинности подсчитать n - число переменных в выражении подсчитать общее число логических операций в
- 22. Решение задач Составить таблицу истинности для формулы
- 23. Решение задач Составить таблицу истинности для формулы
- 25. Скачать презентацию

















 Программы-переводчики
Программы-переводчики Тизерная кухня. (День 6)
Тизерная кухня. (День 6) Системная динамика. Модели и особенности
Системная динамика. Модели и особенности Как записаться на онлайн-курсы на платформе Электронная информационно-образовательная среда НИИ КПССЗ
Как записаться на онлайн-курсы на платформе Электронная информационно-образовательная среда НИИ КПССЗ Эталонная семиуровневая модель OSI
Эталонная семиуровневая модель OSI Программное обеспечение компьютера
Программное обеспечение компьютера Решение задач с ветвлением
Решение задач с ветвлением Электронные таблицы
Электронные таблицы Komprese RLE v Matlabu Reprezentace signálu
Komprese RLE v Matlabu Reprezentace signálu Российские телеканалы
Российские телеканалы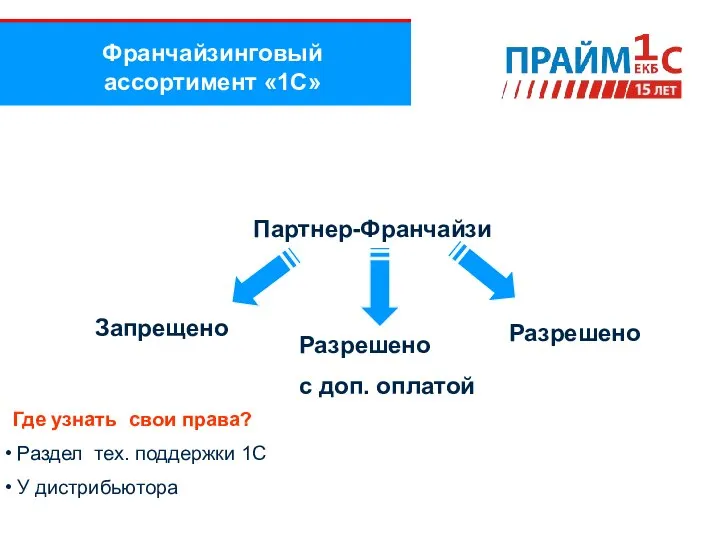 Франчайзинговый ассортимент 1С
Франчайзинговый ассортимент 1С 30 сентября - профессиональный праздник всех пользователей и работников Интернет-индустрии. Международный День Интернета
30 сентября - профессиональный праздник всех пользователей и работников Интернет-индустрии. Международный День Интернета Информационный процесс
Информационный процесс Программирование на языке Python
Программирование на языке Python Аппаратная реализация компьютера
Аппаратная реализация компьютера Изображения. Урок 6
Изображения. Урок 6 Материалы курса Система автоматического программирования. Основные принципы & Подводные камни
Материалы курса Система автоматического программирования. Основные принципы & Подводные камни Информационная система федерального института промышленной собственности РФ
Информационная система федерального института промышленной собственности РФ Операционные системы
Операционные системы Таргетированная реклама
Таргетированная реклама Шерман Кент - батько OSINT
Шерман Кент - батько OSINT Системный анализ и моделирование
Системный анализ и моделирование Многотабличные базы данных. Связывание таблиц
Многотабличные базы данных. Связывание таблиц HTML (HyperText Markup Language, язык разметки гипертекста)
HTML (HyperText Markup Language, язык разметки гипертекста) Практикум. Операторы цикла
Практикум. Операторы цикла Введение в WCF
Введение в WCF Компьютерные презентации
Компьютерные презентации Лекция №5 по курсу ImageView, radioButton, интенты
Лекция №5 по курсу ImageView, radioButton, интенты