Арифметические операции в позиционных системах счисления

Арифметические операции в позиционных системах счисления

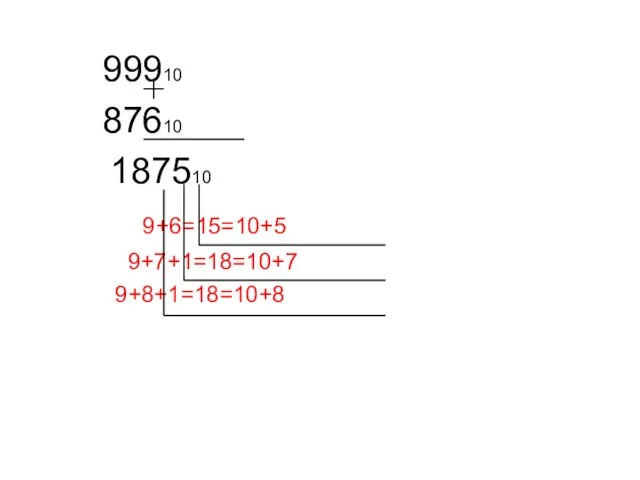
99910
87610
187510
9+6=15=10+5
9+7+1=18=10+7
9+8+1=18=10+8

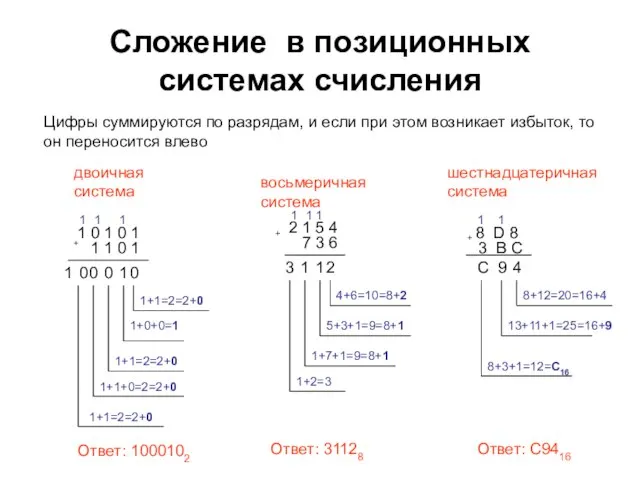
Сложение в позиционных системах счисления
Цифры суммируются по разрядам, и если при этом возникает избыток, то он переносится влево
1 0 1 0 1
+
1 1 0 1
двоичная
система
0
1+1=2=2+0
1
1
1+0+0=1
0
1+1=2=2+0
1
0
1+1+0=2=2+0
1
0
1+1=2=2+0
1
Ответ: 1000102
2 1 5 4
+
7 3 6
2
4+6=10=8+2
1
1
5+3+1=9=8+1
1
1+7+1=9=8+1
1
3
1+2=3
восьмеричная
система
1
Ответ: 31128
шестнадцатеричная
система
8 D 8
+
3 B C
4
8+12=20=16+4
1
9
13+11+1=25=16+9
8+3+1=12=C16
C
1
Ответ: C9416

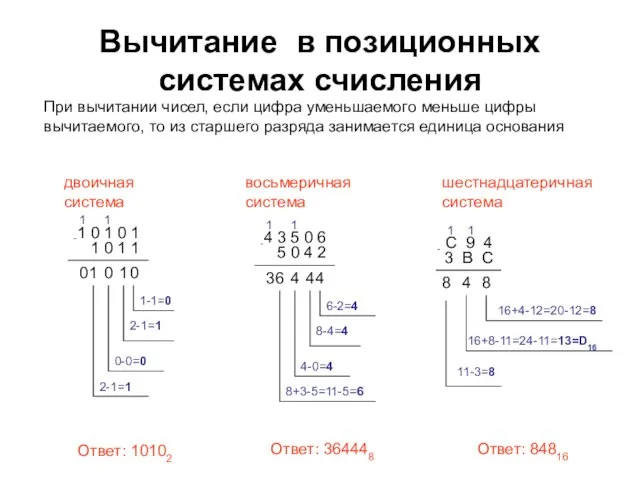
Вычитание в позиционных системах счисления
При вычитании чисел, если цифра уменьшаемого меньше цифры вычитаемого, то из старшего разряда занимается единица основания
двоичная
система
Ответ: 10102
восьмеричная
система
Ответ: 364448
шестнадцатеричная
система
Ответ: 84816
1 0 1 0 1
-
1 0 1 1
0
1-1=0
1
1
2-1=1
0
0-0=0
1
2-1=1
1
0
4 3 5 0 6
-
5 0 4 2
4
6-2=4
1
4
8-4=4
4
4-0=4
6
8+3-5=11-5=6
1
3
С 9 4
-
3 В С
8
16+4-12=20-12=8
1
4
16+8-11=24-11=13=D16
8
11-3=8
1

Умножение в позиционных системах счисления
При умножении многозначных чисел в различных позиционных системах применяется алгоритм перемножения чисел в столбик, но при этом результаты умножения и сложения записываются с учетом основания системы счисления
двоичная
система
Ответ: 1010111112
восьмеричная
система
Ответ: 133518
1 1 0 1 1
х
1 1 0 1
1 1 0 1 1
1 1 0 1 1
1 1 0 1 1
1 0 1 0 1 1 1 1 1
1+1+1=3=2+1
1
1+1+1=3=2+1
1
1+1=2=2+0
1
1
1 6 3
х
6 3
5 3 1
1
2
1 2 6 2
2
4
1 3 3 5 1
1

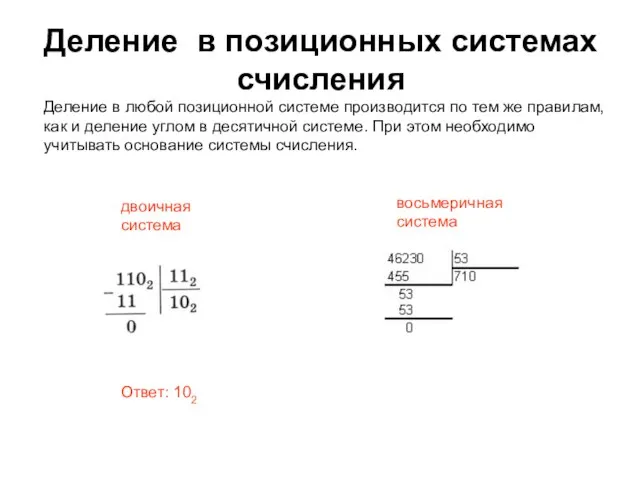
Деление в позиционных системах счисления
Деление в любой позиционной системе производится по тем же правилам, как и деление углом в десятичной системе. При этом необходимо учитывать основание системы счисления.
двоичная
система
Ответ: 102
восьмеричная
система

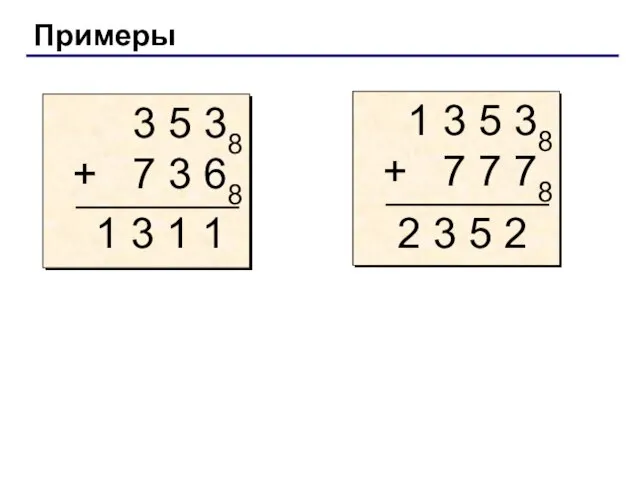
Примеры
1 3 1 1
2 3 5 2

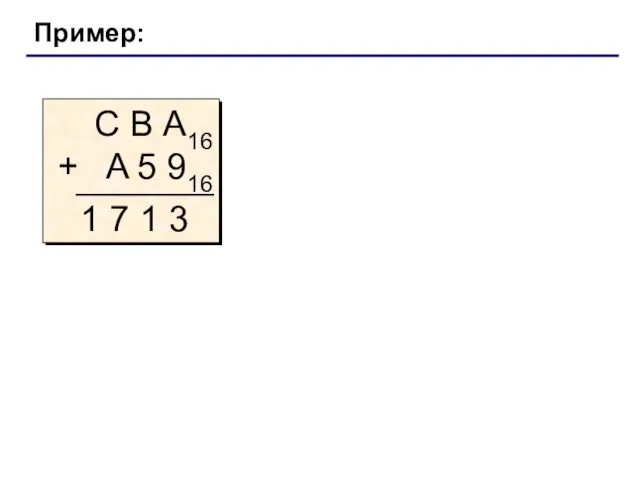
Пример:
С В А16
+ A 5 916
1 7 1 3

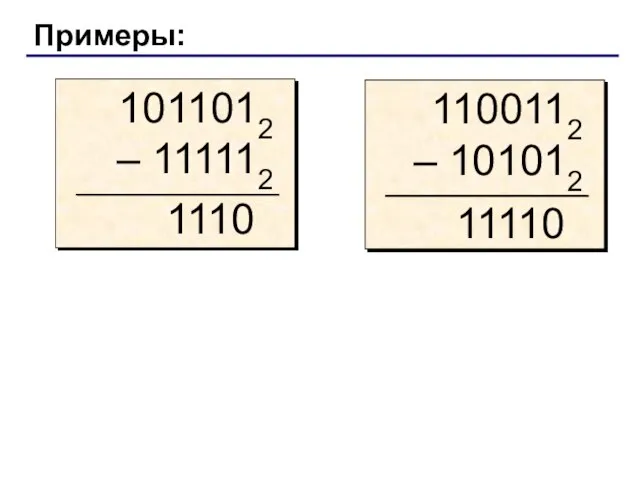
Примеры:
1110
11110

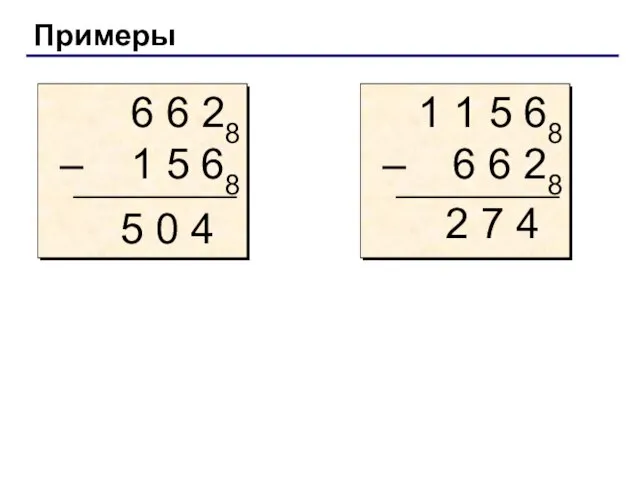
Примеры
5 0 4
2 7 4

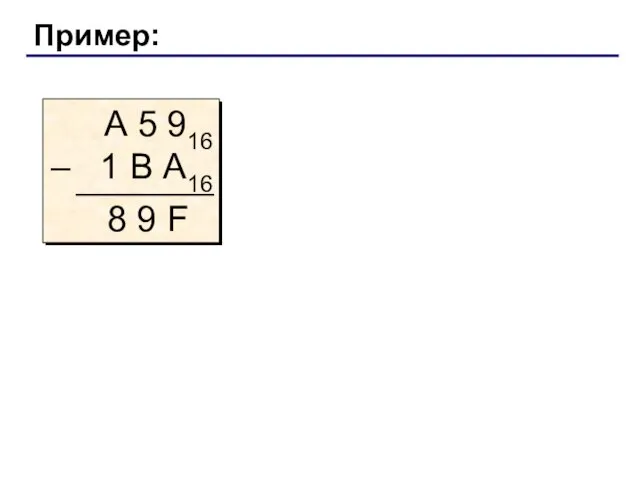
Пример:
А 5 916
– 1 В А16
8 9 F

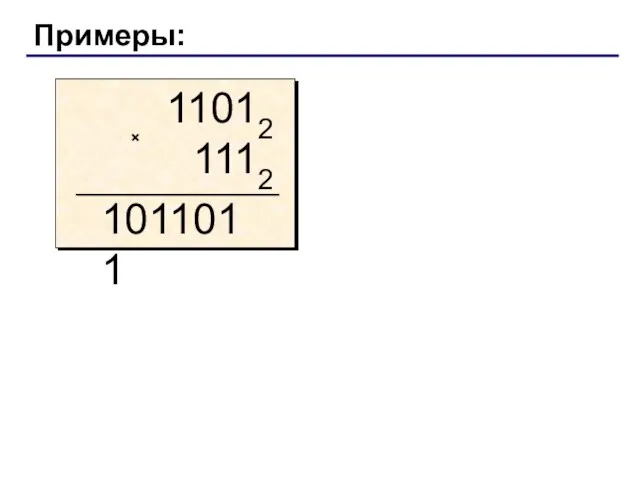
Примеры:
×
1011011

Домашнее задание
1. Уровень знания:
Знать алгоритмы выполнения арифметических действий в позиционных системах счисления
2.Уровень понимания: Выполните действия:
А) Выполнить вычитание:
а) 1100000011,011(2) - 101010111,1(2)
б) 1510,2(8) - 1230,54(8)
в) 27D,D8(16) - 191,2(16)
Б) 3. Сложить числа:
а) 10000000100(2) + 111000010(2)
б) 223,2(8) + 427,54(8)
в) 3B3,6(16) + 38B,4(16)
3.Творческий уровень: Восстановите двоичные цифры:
**0*0*1**1+10111*1011=100*1*00010;
1*01+1**=10100.