Асимметричные алгоритмы. Лекция №7

У Г А Т У
Содержание лекции
Уфимский государственный авиационный технический университет
Базовые операции асимметричной криптографии
Генерация случайных простых чисел
Операции по модулю целого числа
Поля, группы, подгруппы
Контроль правильности вычислений
Алгоритм Диффи-Хеллмана
Алгоритм RSA
Алгоритм DSA

У Г А Т У
Общие сведения
Уфимский государственный авиационный технический университет
Асимметричная криптография

У Г А Т У
Генерация случайных простых чисел
Уфимский государственный авиационный технический университет
Частота простых чисел уменьшается с порядком
В промежутке между числами n/2 и n вероятность, что случайное число будет простым, составляет примерно 1/ln(n)
Пример: вероятность, что случайное число длиной 2000 бит будет простым, составляет ~1/1386
В асимметричной криптографии используются простые числа длиной 1024-4096 бит (алгоритм RSA) или 2048-8192 бит (алгоритм Диффи-Хеллмана)
Генерируются случайные нечетные числа в нужном диапазоне и проверяются на простоту
При генерации в старший и младший биты записываются единицы, в остальные биты записываются случайные данные
Проверка случайного числа на простоту:
Проверяется, делится ли оно на числа из списка малых простых чисел
Если нет, то число проверяется с помощью теста Рабина-Миллера

У Г А Т У
Генерация случайных простых чисел
Уфимский государственный авиационный технический университет Список малых простых чисел

У Г А Т У
Генерация случайных простых чисел
Уфимский государственный авиационный технический университет Тест Рабина-Миллера

У Г А Т У
Генерация случайных простых чисел
Уфимский государственный авиационный технический университет Тест Рабина-Миллера
Выбирается случайное число a (базис) от 2 до p и выполняется проверка:
i = 0;
v = a^s mod p; // наиболее ресурсозатратная операция
ЕСЛИ v = 1 ТО ПРОВЕРКА ПРОЙДЕНА
ИНАЧЕ ПОКА v != t – 1
ЕСЛИ i = t – 1 ТО ПРОВЕРКА НЕ ПРОЙДЕНА
ИНАЧЕ
v = v^2 mod p;
i = i + 1;
КОНЕЦ
КОНЕЦ
ПРОВЕРКА ПРОЙДЕНА

У Г А Т У
Операции по модулю целого числа
Уфимский государственный авиационный технический университет
Запись 8 mod 7 = 1 равнозначна записи 8 = 1 mod 7
Если модуль является степенью 2, то при сложении/вычитании/умножении достаточно игнорировать разряды старше чем двоичный логарифм модуля
Сложение/вычитание – достаточно выполнить операцию в целых числах, а затем (если нужно) один раз отнять или прибавить модуль

У Г А Т У
Операции по модулю целого числа
Уфимский государственный авиационный технический университет
Умножение

У Г А Т У
Операции по модулю целого числа
Уфимский государственный авиационный технический университет
Умножение Монгомери

У Г А Т У
Операции по модулю целого числа
Уфимский государственный авиационный технический университет
Деление по модулю
При делении используется расширенный алгоритм Евклида для поиска наибольшего общего делителя двух чисел
Для входных чисел a и b алгоритм возвращает 3 параметра: d (НОД a и b), u и v, удовлетворяющие условию d = ua + vb
Результат деления вычисляется по формуле: a/b mod p = a*u mod p
Расширенный алгоритм Евклида:
a1 = a; b1 = b; u_a = 1; v_a = 0; u_b = 0; v_b = 1;
ПОКА а1 != 0
q = b1 / a1;
[ a1; b1 ] = [ b1-q*a1; a1 ];
[ u_a; v_a; u_b; v_b ] = [ u_b-q*u_a; v_b-q*v_a; u_a; v_a ]
d = b1; u = u_b; v = v_b;
Выполнимо не всегда, но для простых модулей работает

У Г А Т У
Операции по модулю целого числа
Уфимский государственный авиационный технический университет
Возведение в натуральную степень по модулю простого числа

У Г А Т У
Операции по модулю целого числа
Уфимский государственный авиационный технический университет
Возведение в натуральную степень по модулю простого числа

У Г А Т У
Операции по модулю целого числа
Уфимский государственный авиационный технический университет
Возведение в натуральную степень по модулю простого числа

У Г А Т У
Поля, группы, подгруппы
Уфимский государственный авиационный технический университет

У Г А Т У
Контроль правильности вычислений
Уфимский государственный авиационный технический университет
Специализированные библиотеки позволяют относительно быстро производить арифметические операции над большими числами
Как правило содержат низкоуровневый код, оптимизирующий вычисления на конкретной аппаратной платформе
Ошибки в вычислениях могут привести к уязвимостям
Проблема тестирования: работа кода зависит от самих данных, а разнообразие вариантов больше, чем можно протестировать
Подход: вупинг
Вычисления дублируются по модулю случайного секретного простого числа t обычно длиной 32, 64 или128 бит
После каждой операции проверяется, что ее результат, взятый по mod t равен результату дублированных вычислений
Вероятность, что при вупинге не будет обнаружена случайная ошибка, примерно равна 1/t

У Г А Т У
Содержание лекции
Уфимский государственный авиационный технический университет
Базовые операции асимметричной криптографии
Алгоритм Диффи-Хеллмана
Описание алгоритма
Выбор параметров
Алгоритм RSA
Алгоритм DSA

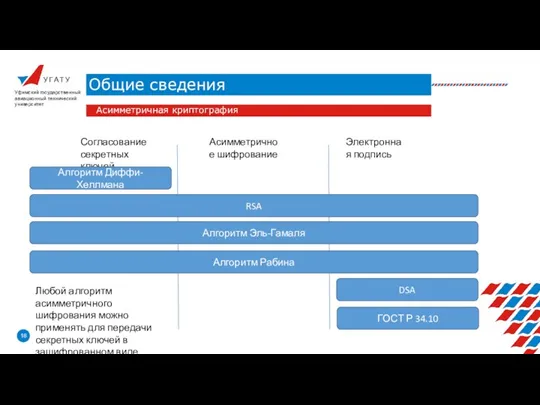
У Г А Т У
Общие сведения
Уфимский государственный авиационный технический университет
Асимметричная криптография
Согласование секретных ключей
Асимметричное шифрование
Электронная подпись
Алгоритм Диффи-Хеллмана
RSA
Алгоритм Эль-Гамаля
Алгоритм Рабина
DSA
ГОСТ Р 34.10
Любой алгоритм асимметричного шифрования можно применять для передачи секретных ключей в зашифрованном виде

У Г А Т У
Алгоритм Диффи-Хеллмана
Уфимский государственный авиационный технический университет

У Г А Т У
Алгоритм Диффи-Хеллмана
Уфимский государственный авиационный технический университет

У Г А Т У
Алгоритм Диффи-Хеллмана
Уфимский государственный авиационный технический университет
Выбор параметров: подгруппа с заданным порядком

У Г А Т У
Алгоритм Диффи-Хеллмана
Уфимский государственный авиационный технический университет
Выбор параметров: подгруппа с заданным порядком

У Г А Т У
Алгоритм Диффи-Хеллмана
Уфимский государственный авиационный технический университет
Выбор параметров: подгруппа с заданным порядком

У Г А Т У
Содержание лекции
Уфимский государственный авиационный технический университет
Базовые операции асимметричной криптографии
Алгоритм Диффи-Хеллмана
Алгоритм RSA
Описание алгоритма
Особенности практической реализации
Распределение ключей с помощью RSA
Алгоритм DSA

У Г А Т У
Алгоритм RSA
Уфимский государственный авиационный технический университет
Генерация ключей

У Г А Т У
Алгоритм RSA
Уфимский государственный авиационный технический университет
Зашифровка и расшифровка
Постановка и проверка электронной подписи

У Г А Т У
Алгоритм RSA
Уфимский государственный авиационный технический университет
Особенности практической реализации
Значение e выбирается небольшим (часто e=3 для ЭП и е=5 для шифрования), чтобы снизить ресурсоемкость вычислений
Под ОК понимается n
Зашифрование и проверка ЭП намного менее ресурсозатратны, чем расшифование и постановка ЭП
Разный показатель для шифрования и подписи позволяет шифровать текст, а затем его подписывать; иначе подписывание равнозначно расшифровке
Зная n и любой из параметров {p,q,t,d} можно рассчитать оставшиеся 3 параметра из {p,q,t,d}
Расшифровку ШТ (постановку ЭП) можно ускорить примерно в 3-4 раза, зная p и q и используя теорему Сунь Цзы (китайскую теорему об остатках [Chinese Remainder Theorem, CRT])

У Г А Т У
Алгоритм RSA
Уфимский государственный авиационный технический университет
Особенности практической реализации

У Г А Т У
Алгоритм RSA
Уфимский государственный авиационный технический университет
Особенности практической реализации

У Г А Т У
Алгоритм RSA
Уфимский государственный авиационный технический университет
Особенности практической реализации
Блок шифруемого текста должен иметь чуть меньшую длину, чем n
Если намного меньше – для расшифровки будет достаточно взять корень 5-й степени из ШТ
Блок шифруемого текста перед шифрованием должен быть преобразован к псевдослучайному виду
Например – побитное сложение с солью
При постановке ЭП сначала вычисляется хеш-функция от документа, затем ставится подпись на эту хеш-функцию
Чтобы достичь необходимой длины блока на основе хеш-функции можно сгенерировать ПСП
либо применить KDF, позволяющую варьировать длину выходного значения

У Г А Т У
Алгоритм RSA
Уфимский государственный авиационный технический университет
Особенности практической реализации

У Г А Т У
Алгоритм RSA
Уфимский государственный авиационный технический университет
Использование для распределения ключей
Асимметричное шифрование применяется для передачи ключа симметричного шифрования
Алиса генерирует случайный блок ОТ, зашифровывает его с помощью RSA на ОК Боба и передает ШТ Бобу
Боб расшифровывает блок своим ЗК
Алиса и Боб генерируют ключ симметричного шифрования на основе переданного блока с помощью KDF
Даже если Еве станет известен ключ симметричного шифрования, это не даст ей информации о ЗК Боба

У Г А Т У
Содержание лекции
Уфимский государственный авиационный технический университет
Базовые операции асимметричной криптографии
Алгоритм Диффи-Хеллмана
Алгоритм RSA
Алгоритм DSA

У Г А Т У
Алгоритм DSA
Уфимский государственный авиационный технический университет

У Г А Т У
Алгоритм DSA
Уфимский государственный авиационный технический университет