Слайд 2Условие
Даны следующие данные:
С – Зашифрованное сообщение
N – Модуль
E – Публичная экспонента
Задача:
Найти исходное

сообщение
Слайд 3Наше решение, главным образом, является реализацией атаки Винера, основанное на предположении, что

закрытый ключ – d слишком мал. Как оказалось в итоге, так оно и было.
Сейчас мы разберём каждую из реализованных функций.
Слайд 4isPerfectSqr(int)
Главным образом функция даёт ответ на вопрос: “Является ли её аргумент идеальным

квадратом?” (Это понадобится позже)
Работает следующим образом:
Функция считает число «х», равное половине аргумента
Работа цикла «While» будет идти до тех пор пока «х ^ 2» не будет равно аргументу либо «х» не повторится (все проверенные значения хранятся во множестве «seen»)
Каждое следующее «х» вычисляется по приведённой формуле, такой подход обеспечивает эффективное выполнение функции, или, другими словами, более быстрое выполнение при достаточно больших значениях аргумента, в сравнении с методом простого перебора.
Слайд 5rational_to_contfrac(e, n)
Функция занимается задачей разложения дроби, где числитель – первый аргумент функции,

знаменатель – второй, в цепную дробь; возвращает список-итератор.
Принцип работы следующий:
Цикл «while» работает до тех пор, пока переменная «e» не обратится в нуль.
Вычисляем «а» - остаток от деления аргументов
Меняем значение переменных-аргументов, следуя алгоритму Евклида. Таким образом мы будем делить делитель на остаток
Слайд 6contfrac_to_rational_iter(contfrac)
Данная функция является, в какой-то степени, логическим продолжением предыдущей и вычисляет «подходящие

дроби» используя циклическую дробь, вычисленную предыдущей функцией. Для этого используются рекурентные соотношения теории чисел, которые можно видеть внутри цикла «for» на слайде. Возвращает итератор-кортеж, где первая компонента – числитель, вторая – знаменатель.
Слайд 7convergents_from_contfrac(contfrac)
Хз, что эта штучка делает и как работает(

Слайд 8Для рассмотрения следующей функции необходимо провести следующие рассуждения:
Знаем, что e * d

= 1 (mod phi), phi = НОК(p – 1, q - 1)
Значит существует целое K: e * d = K * phi + 1
Пусть G = НОД(p – 1, q - 1), тогда e * d = (K / G) * phi + 1
Обозначим k = K / НОД(K, G), g = G / НОД(K, G)
Получаем следующее: e * d = (k / g) * phi + 1
Или e * d * g = k * (p – 1)(q – 1) + g
Слайд 9get_private_exponent(e, n)
Заключительная функция программы, которая либо вернёт нам искомый закрытый ключ «d»,

либо «0», что означает провал в задаче его поиска.
Принцип работы:
Каждую итерацию цикла «for» высчитываем произведение «e * d * g», phi, исходя из предыдущих рассуждений – предполагая, что «g», или остаток от деления, равен нулю
В последнем случае, следуя алгоритму атаки Винера, проверяем два предположения, которые оба должны оказаться истиной:
«х» / 2 не имеет остатка отличного от нуля, где х = N – phi + 1
(x ^ 2) – N должно являтся идеальным квадратом
3) В случае логической истины при конъюнкции этих двух условий получаем нужный нам закрытый ключ простым арифметическим действием.
Осталось только расшифровать само послание.
Слайд 10Итог
Таким образом при исходных данных:
N = 0x8da7d2ec7bf9b322a539afb9962d4d2ebeb3e3d449d709b80a51dc680a14c87ffa863edfc7b5a2a542a0fa610febe2d967b58ae714c46a6eccb44cd5c90d1cf5e271224aa3367e5a13305f2744e2e56059b17bf520c95d521d34fdad3b0c12e7821a3169aa900c711e6923ca1a26c71fc5ac8a9ff8c878164e2434c724b68b508a030f86211c1307b6f90c0cd489a27fdc5e6190f6193447e0441a49edde165cf6074994ea260a21ea1fc7e2dfb038df437f02b9ddb7b5244a9620c8eca858865e83bab3413135e76a54ee718f4e431c29d3cb6e353a75d74f831bed2cc7bdce553f25b617b3bdd9ef901e249e43545c91b0cd8798b27804d61926e317a2b745
E = 0x86d357db4e1b60a2e9f9f25e2db15204c820b6e8d8d04d29db168c890bc8a6c1e31b9316c9680174e128515a00256b775a1a8ccca9c6936f1b4c2298c03032cda4dd8eca1145828d31466bf56bfcf0c6a8b4a1b2fb27de7a57fae7430048d7590734b2f05b6443ad60d89606802409d2fa4c6767ad42bffae01a8ef1364418362e133fa7b2770af64a68ad50ad8d2bd5cebb99ceb13368fb31a6e7503e753f8638e21a96af1b6498c18578ba89b98d70fa482ad137d28fe701b4b77baa25d5e84c81b26ee9bddf8cbb51a071c60dd57714de379cd4bc14932809ba18524a0a18e4133665cfc46e2c4fcfbc28e0a0957e5513a7307c422b87a6182d0b6a074b4d
C = 0x6a2f2e401a54eeb5dab1e6d5d80e92a6ca189049e22844c825012b8f0578f95b269b19644c7c8af3d544840d380ed75fdf86844aa8976622fa0501eaec0e5a1a5ab09d3d1037e55501c4e270060470c9f4019ced6c4e67673843daf2fd71c64f3dd8939ae322f2b79d283b3382052d076ebe9bb50b0042f1f7dd7beadf0f5686926ade9fc8370283ead781a21896e7a878d99e77c3bb1f470401062c0e0327fd85da1cf12901635f1df310e8f8c7d87aff5a01dbbecd739cd8f36462060d0eb237af8d613e2d9cebb67d612bcfc353ef2cd44b7ac85e471287eb04ae9b388b66ea8eb32429ae96dba5da8206894fa8c58a7440a127fceb5717a2eaa3c29f25f7
Ответом будет

являтся следующее сообщение: crypto{s0m3th1ng5_c4n_b3_t00_b1g}









 Поиск работы. Включаем самоходность
Поиск работы. Включаем самоходность HTML1 (1)
HTML1 (1) Анализ требований к программному обеспечению. Анализ и моделирование функциональной области внедрения программных систем
Анализ требований к программному обеспечению. Анализ и моделирование функциональной области внедрения программных систем Тестирование и отладка программного средства. Отладка ПС
Тестирование и отладка программного средства. Отладка ПС IT-технологии. Роботехника в Политехе
IT-технологии. Роботехника в Политехе Анимация в GIMPг
Анимация в GIMPг Основы программирования. Управление: IF, GOTO, DO WHILE, WHILE, RETURN, CONTINUE, BREAK, SWITCH
Основы программирования. Управление: IF, GOTO, DO WHILE, WHILE, RETURN, CONTINUE, BREAK, SWITCH Всероссийская образовательная акция Урок цифры — 2020. Нейросети и коммуникации
Всероссийская образовательная акция Урок цифры — 2020. Нейросети и коммуникации API как двигатель развития цифрового страхования
API как двигатель развития цифрового страхования Отечественная и зарубежная нормативно-правовая база в области информационной безопасности сетевого оборудования. (Лекция 2)
Отечественная и зарубежная нормативно-правовая база в области информационной безопасности сетевого оборудования. (Лекция 2) Simcenter femap 2022.1
Simcenter femap 2022.1 Понятие алгоритмов, свойства алгоритма
Понятие алгоритмов, свойства алгоритма Алгоритмизация и программирование. Лабораторные работы
Алгоритмизация и программирование. Лабораторные работы Медиа вызов. Забайкальский государственный университет. Факультет филологии и массовых коммуникаций
Медиа вызов. Забайкальский государственный университет. Факультет филологии и массовых коммуникаций Технологии информационного моделирования автомобильных дорог
Технологии информационного моделирования автомобильных дорог Графическая информация в Интернет
Графическая информация в Интернет Всемирная путина (World Wide Web)
Всемирная путина (World Wide Web) SE-2222_DatabaseSecurity
SE-2222_DatabaseSecurity Твой друг — учебник. 3 класс
Твой друг — учебник. 3 класс GNU Linux OS L1
GNU Linux OS L1 Домашняя медиа сеть на основе сервера DLNA
Домашняя медиа сеть на основе сервера DLNA Основные устройства компьютера
Основные устройства компьютера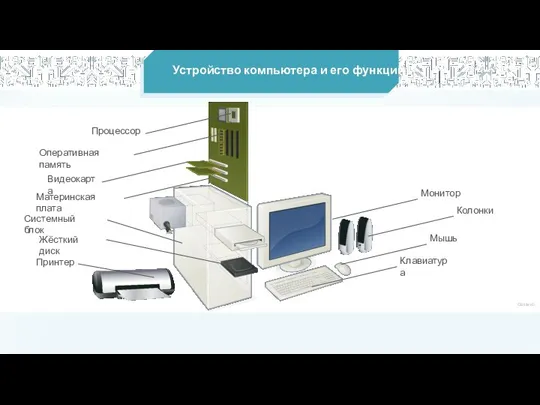 Устройство компьютера и его функции
Устройство компьютера и его функции Анализ данных. Основные принципы
Анализ данных. Основные принципы Живые рисунки на компьютере
Живые рисунки на компьютере Кибербезопасность данных компаний
Кибербезопасность данных компаний Понятие о языках программирования
Понятие о языках программирования Электронные таблицы. Обработка числовой информации в электронных таблицах
Электронные таблицы. Обработка числовой информации в электронных таблицах