Слайд 3ФРАКТАЛ
(лат. fractus — дроблёный, сломанный, разбитый) — математическое множество, обладающее свойством самоподобия, то есть однородности в различных

шкалах измерения.
Слайд 4САМОПОДОБИЕ
САМОПОДОБНЫЙ ОБЪЕКТ
Это объект, в точности или приближённо совпадающий с частью себя самого

(то есть целое имеет ту же форму, что и одна или более частей).
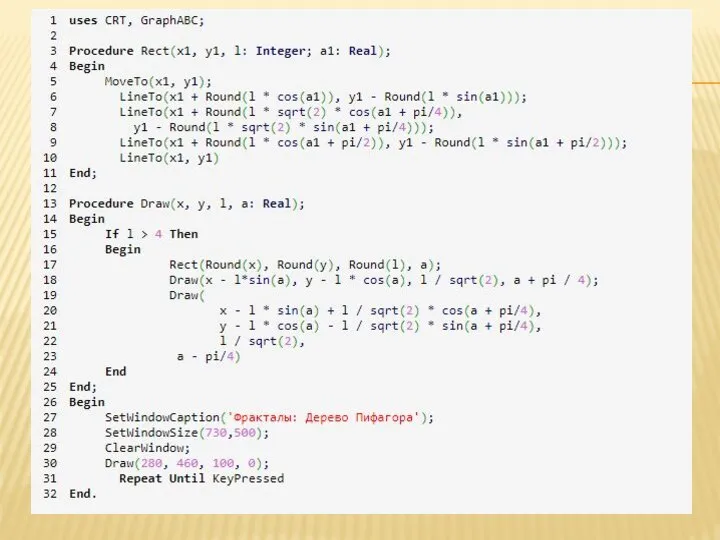
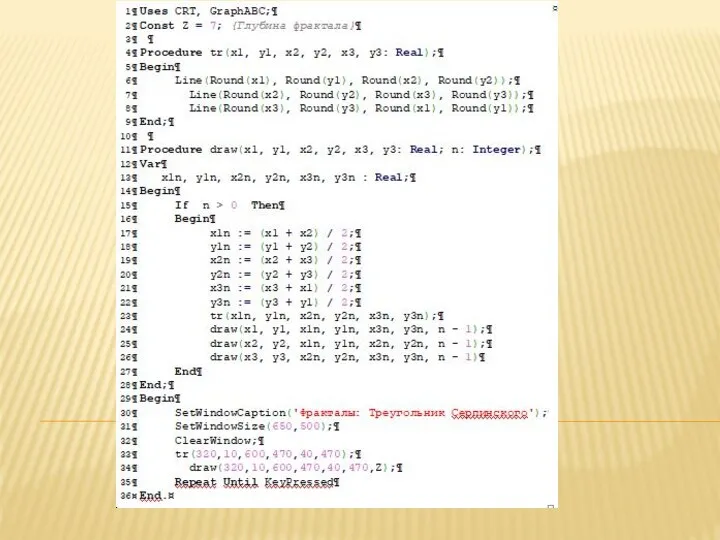
Слайд 5ЯЗЫК ПРОГРАММИРОВАНИЯ ПАСКАЛЬ
Это язык программирования общего назначения. Один из наиболее известных языков

программирования, используется для обучения программированию в школах, ССУЗах, ВУЗах, в дальнейшем он служит базой для ряда других языков.
Слайд 6КЛАССИФИКАЦИЯ ФРАКТАЛОВ
Обладает нетривиальной структурой на всех масштабах.
Является самоподобным или приближенно самоподобным.

Обладает дробной метрической размерностью.
Слайд 7В ОСНОВНОМ:
Алгебраические фракталы .
Геометрические фракталы .
Стохастические фракталы.

Слайд 8АЛГЕБРАИЧЕСКИЕ ФРАКТАЛЫ - ЭТО САМАЯ КРУПНАЯ ГРУППА ФРАКТАЛОВ, ПОЛУЧИВШАЯ НАЗВАНИЕ ЗА ИСПОЛЬЗОВАНИЕ

АЛГЕБРАИЧЕСКИХ ФОРМУЛ.
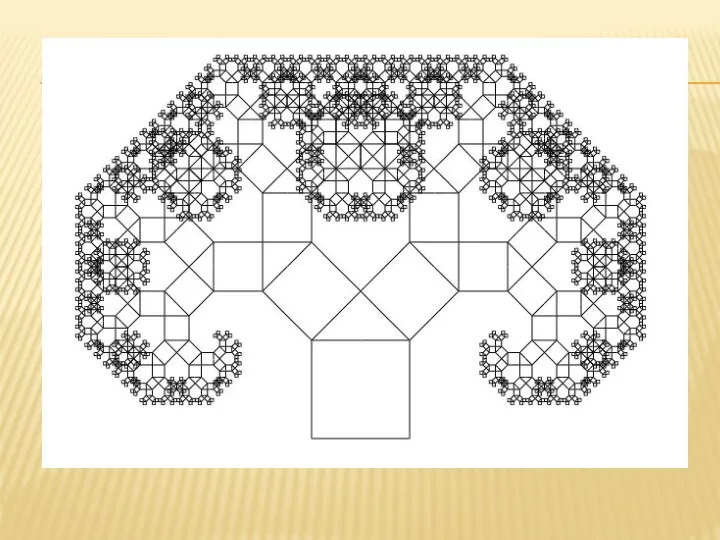
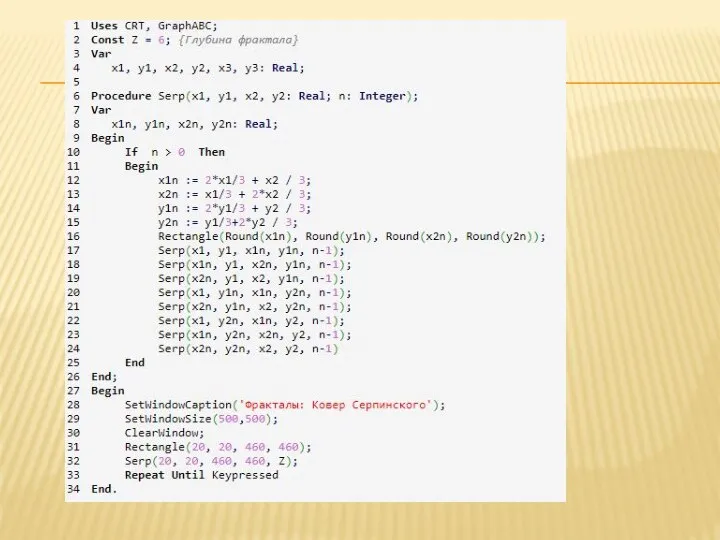
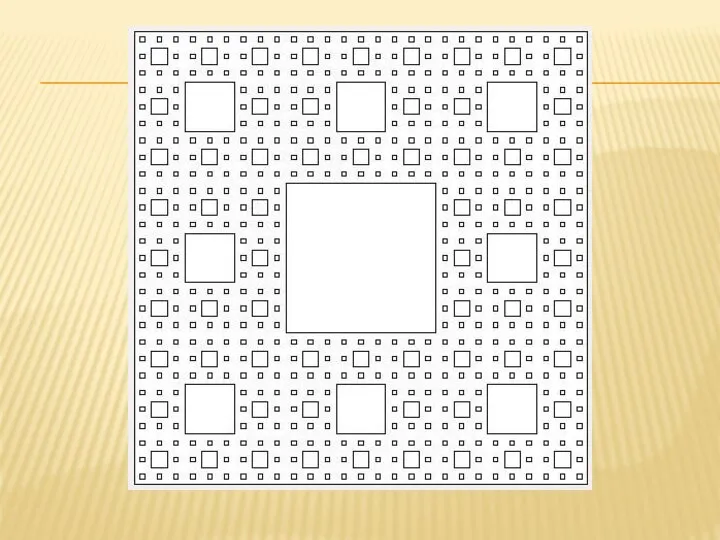
Слайд 9ГЕОМЕТРИЧЕСКИЕ ФРАКТАЛЫ- ЭТОТ ТИП ФРАКТАЛОВ ПОЛУЧАЕТСЯ ПУТЕМ ПРОСТЫХ ГЕОМЕТРИЧЕСКИХ ПОСТРОЕНИЙ.

Слайд 10СТОХАСТИЧЕСКИЕ ФРАКТАЛЫ - ЭТО ВИД ФРАКТАЛОВ, КОТОРЫЙ ПОЛУЧАЮТСЯ В ТОМ СЛУЧАЕ, ЕСЛИ

В ИТЕРАЦИОННОМ ПРОЦЕССЕ СЛУЧАЙНЫМ ОБРАЗОМ МЕНЯТЬ КАКИЕ-ЛИБО ЕГО ПАРАМЕТРЫ.












 Разработка структуры программы и модульное программирование
Разработка структуры программы и модульное программирование Blockly
Blockly Проектирование сети поставщика интернет-услуг
Проектирование сети поставщика интернет-услуг Трассировка пиксельных изображений
Трассировка пиксельных изображений Виртуальные технологии в образовании
Виртуальные технологии в образовании Персональный компьютер
Персональный компьютер Подготовка Семантики
Подготовка Семантики Интернет-маркетинг для чайников
Интернет-маркетинг для чайников Web-страницы. Язык HTML
Web-страницы. Язык HTML Является ли компьютерная графика искусством?
Является ли компьютерная графика искусством? Представление вещественных чисел
Представление вещественных чисел Сборки. Атрибуты
Сборки. Атрибуты Использование Google forms в работе с родителями ДОУ
Использование Google forms в работе с родителями ДОУ Жанр и метод интервью
Жанр и метод интервью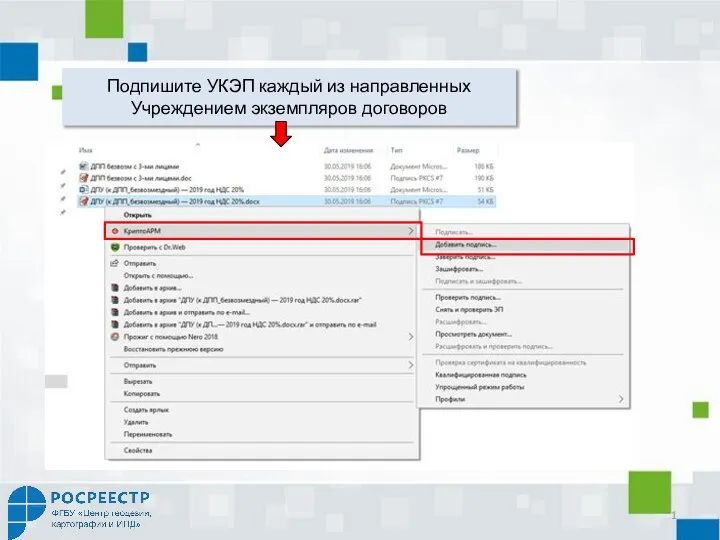 Как подписать договор с двух сторон
Как подписать договор с двух сторон События объекта TForm. Управление с клавиатуры. Lazarus. Урок 16
События объекта TForm. Управление с клавиатуры. Lazarus. Урок 16 Модульная сетка. Современные компьютерные дизайн-программы
Модульная сетка. Современные компьютерные дизайн-программы Информационный лабиринт. Игра
Информационный лабиринт. Игра Бренд (Торговая марка/Знак места обслуживания)
Бренд (Торговая марка/Знак места обслуживания) Тест по программированию
Тест по программированию Spółka zajmuje się dostarczaniem rozwiązań softweare dla małych i średnich przedsiębiorstw
Spółka zajmuje się dostarczaniem rozwiązań softweare dla małych i średnich przedsiębiorstw 3_1_Elementy_upravlenia
3_1_Elementy_upravlenia Графические информационные модели. Графы. Моделирование и формализация
Графические информационные модели. Графы. Моделирование и формализация Всемирная путина (World Wide Web)
Всемирная путина (World Wide Web) Игра Да-нет. Информатика
Игра Да-нет. Информатика Платформа Quotex. Настройки
Платформа Quotex. Настройки Продвижение образовательных услуг Инстаграм
Продвижение образовательных услуг Инстаграм Регистрация на Портале РКЦ
Регистрация на Портале РКЦ