ИДЗ. Алгоритм Дейкстры

Задание.
Решение.
Найдем объединение множеств А и В – множество, состоящее из элементов, входящих хотя бы в одно из множеств А или В:
AUB={0,1,3,4,5,6} .

Задание.
Решение.

Задание.
Решение.

Задание.
Решение.
4) Найдем множество D={2,7,4,6}.

Задание.

Задание.
Решение.

Задание.
C\B={1,2}.
D={2}.

Задание.

Алгоритм Дейкстры
Алгори́тм Де́йкстры (англ. Dijkstra’s algorithm) — алгоритм на графах, изобретённый нидерландским учёным Эдсгером Дейкстрой в 1959 году. Находит кратчайшие пути от одной из вершин графа до всех остальных. Алгоритм работает только для графов без рёбер отрицательного веса. Алгоритм широко применяется в программировании и технологиях, например, его используют протоколы маршрутизации OSPF и IS-IS.
Примеры
Вариант 1. Дана сеть автомобильных дорог, соединяющих города Московской области. Некоторые дороги односторонние. Найти кратчайшие пути от города Москвы до каждого города области (если двигаться можно только по дорогам).
Вариант 2. Имеется некоторое количество авиарейсов между городами мира, для каждого известна стоимость. Стоимость перелёта из A в B может быть не равна стоимости перелёта из B в A. Найти маршрут минимальной стоимости (возможно, с пересадками) от Копенгагена до Барнаула.

Задание.

Алгоритм Дейкстры
Каждой вершине из V сопоставим метку — минимальное известное расстояние от этой вершины до a.
Алгоритм работает пошагово — на каждом шаге он «посещает» одну вершину и пытается уменьшать метки.
Работа алгоритма завершается, когда все вершины посещены.
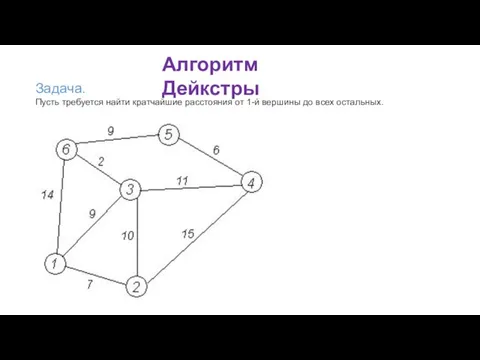
Инициализация.
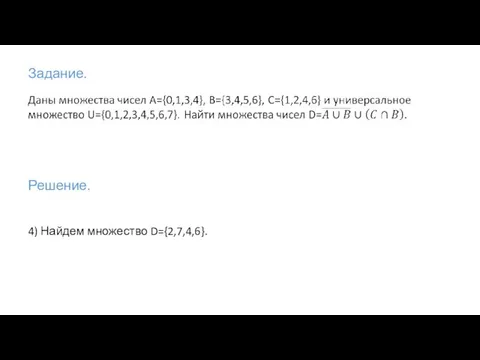
Метка самой вершины a полагается равной 0, метки остальных вершин — бесконечности.
Это отражает то, что расстояния от a до других вершин пока неизвестны.
Все вершины графа помечаются как непосещённые.
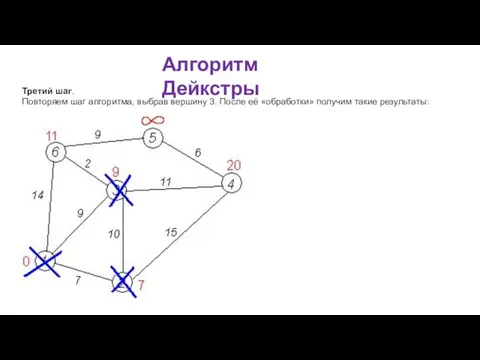
Шаг алгоритма.
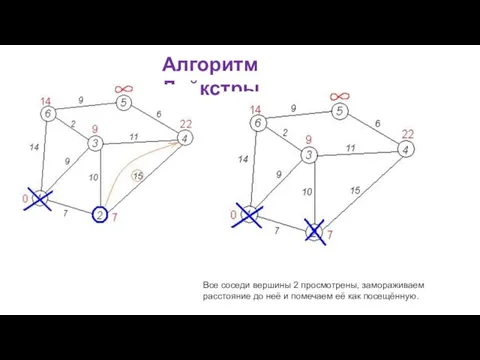
Если все вершины посещены, алгоритм завершается.
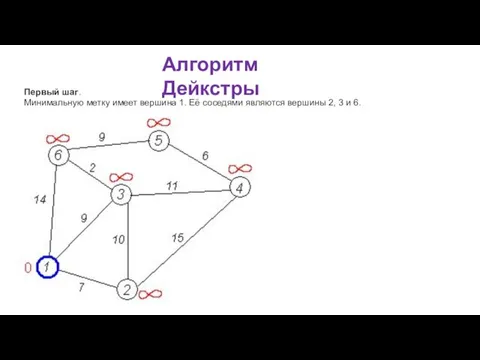
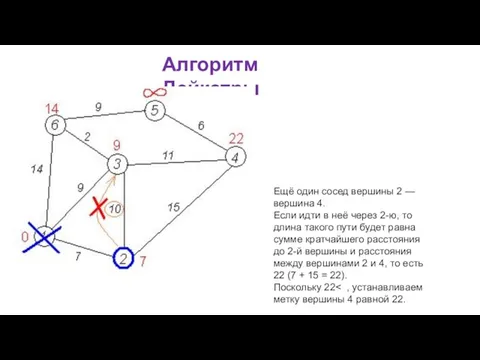
В противном случае, из ещё не посещённых вершин выбирается вершина u, имеющая минимальную метку.
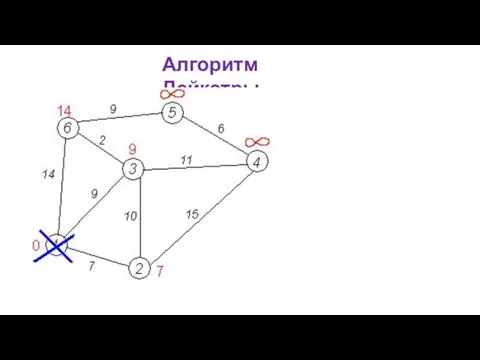
Мы рассматриваем всевозможные маршруты, в которых u является предпоследним пунктом. Вершины, в которые ведут рёбра из u, назовём соседями этой вершины. Для каждого соседа вершины u, кроме отмеченных как посещённые, рассмотрим новую длину пути, равную сумме значений текущей метки u и длины ребра, соединяющего u с этим соседом.
Если полученное значение длины меньше значения метки соседа, заменим значение метки полученным значением длины. Рассмотрев всех соседей, пометим вершину u как посещённую и повторим шаг алгоритма.

Алгоритм Дейкстры
Задача.
Пусть требуется найти кратчайшие расстояния от 1-й вершины до всех остальных.

Алгоритм Дейкстры
Кружками обозначены вершины, линиями — пути между ними (рёбра графа).
В кружках обозначены номера вершин, над рёбрами обозначен их вес — длина пути.
Рядом с каждой вершиной красным обозначена метка — длина кратчайшего пути в эту вершину из вершины 1.

Алгоритм Дейкстры
Первый шаг.
Минимальную метку имеет вершина 1. Её соседями являются вершины 2, 3 и 6.

Алгоритм Дейкстры
Первый по очереди сосед вершины 1 — вершина 2, потому что длина пути до неё минимальна.
Длина пути в неё через вершину 1 равна сумме значения метки вершины 1 и длины ребра, идущего из 1-й в 2-ю, то есть 0 + 7 = 7.
Это меньше текущей метки вершины 2, бесконечности, поэтому новая метка 2-й вершины равна 7.

Алгоритм Дейкстры
Аналогичную операцию проделываем с двумя другими соседями 1-й вершины — 3-й и 6-й.
Все соседи вершины 1 проверены.
Текущее минимальное расстояние до вершины 1 считается окончательным и пересмотру не подлежит.
Вычеркнем её из графа, чтобы отметить, что эта вершина посещена.

Алгоритм Дейкстры

Алгоритм Дейкстры
Второй шаг.
Снова находим «ближайшую» из непосещённых вершин. Это вершина 2 с меткой 7.
Снова пытаемся уменьшить метки соседей выбранной вершины, пытаясь пройти в них через 2-ю вершину. Соседями вершины 2 являются вершины 1, 3 и 4.
Первый (по порядку) сосед вершины 2 — вершина 1. Но она уже посещена, поэтому с 1-й вершиной ничего не делаем.
Следующий сосед — вершина 3, так как имеет минимальную метку.
Если идти в неё через 2, то длина такого пути будет равна 17 (7 + 10 = 17). Но текущая метка третьей вершины равна 9, а это меньше 17, поэтому метка не меняется.

Алгоритм Дейкстры
Ещё один сосед вершины 2 — вершина 4.
Если идти в неё через 2-ю, то длина такого пути будет равна сумме кратчайшего расстояния до 2-й вершины и расстояния между вершинами 2 и 4, то есть 22 (7 + 15 = 22).
Поскольку 22< , устанавливаем метку вершины 4 равной 22.

Алгоритм Дейкстры
Все соседи вершины 2 просмотрены, замораживаем расстояние до неё и помечаем её как посещённую.

Алгоритм Дейкстры
Третий шаг.
Повторяем шаг алгоритма, выбрав вершину 3. После её «обработки» получим такие результаты:

Алгоритм Дейкстры
Дальнейшие шаги.
Повторяем шаг алгоритма для оставшихся вершин. Это будут вершины 6, 4 и 5, соответственно порядку.
Завершение выполнения алгоритма.
Алгоритм заканчивает работу, когда все вершины посещены.
Результат работы алгоритма виден на последнем рисунке: кратчайший путь от вершины 1 до 2-й составляет 7, до 3-й — 9, до 4-й — 20, до 5-й — 20, до 6-й — 11.