Искусственный интеллект в сетях связи. Лекция 2. Архитектура искусственных нейронных сетей

Биологические и искусственные нейронные сети
Искусственные нейронные сети (ИНС) — математические модели, а также их программные или аппаратные реализации, построенные по принципу организации и функционирования биологических нейронных сетей.
Биологическая нейронная сеть — совокупность нейронов, которые связаны или функционально объединены в нервной системе, выполняют специфические физиологические функции.

Биологические и искусственные нейронные сети
Модели искусственных нейронных сетей были вдохновлены биологическими нейронными сетями, хотя биологические нейронные сети в настоящий момент являются заметно более сложными и масштабными системами.
При этом в области искусственного интеллекта используются не только идеи из биологических НС, но и другие математические модели.

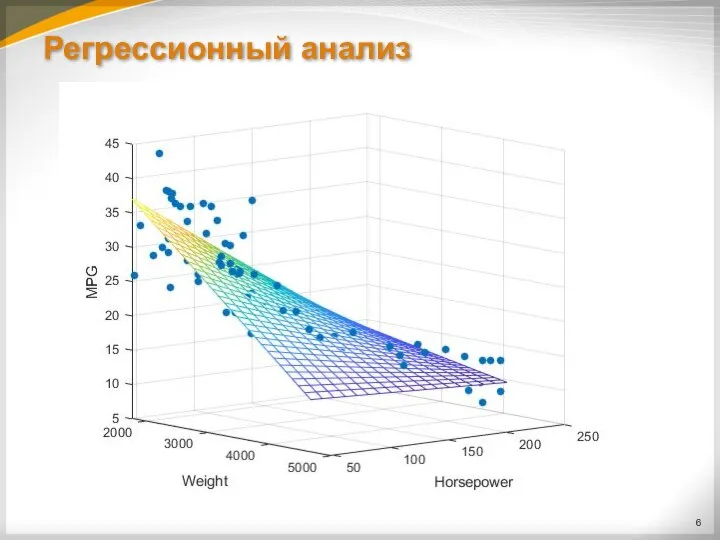
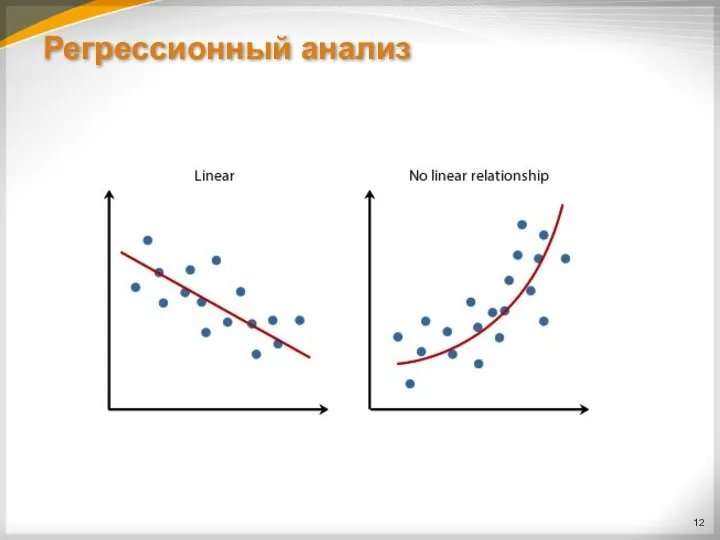
Регрессионный анализ
Регрессионный анализ — статистический метод исследования влияния одной или нескольких независимых переменных X1, X2, ..., XM на зависимую переменную Y.
Независимые переменные — регрессоры, предикторами.
Зависимая переменная — критериальная переменная.
Пример: влияние средней годовой температуры и уровня осадков в винодельческом регионе на стоимость вина.

Регрессионный анализ
Регрессионный анализ — статистический метод исследования влияния одной или нескольких независимых переменных X1, X2, ..., XM на зависимую переменную Y:
Y= f (X1, X2, ..., XM)
X1, X2, ..., XM – независимые переменные (регрессоры, предикторы).
Y – зависимая (критериальная) переменная.
f – функция регрессии

Регрессионный анализ

Регрессионный анализ
Каким образом можно определить функцию регрессии?
Классический подход — метод наименьших квадратов.
Суть метода заключается в подсчете квадрата разницы между реальным значением Yk и вычисленным с помощью модели значением Y’k для каждого измеренного значения и нахождении такой функции регрессии, при которых сумма этих квадратов разниц минимальна:

Регрессионный анализ
Метод наименьших квадратов реализован:
в виде библиотек в некоторых языках программирования со статистическим уклоном (Python + Numpy&Scipy, R);
в MatLab и подобных программах;
и даже в виде ондайн-калькуляторов —
http://math.semestr.ru/regress/corel.php

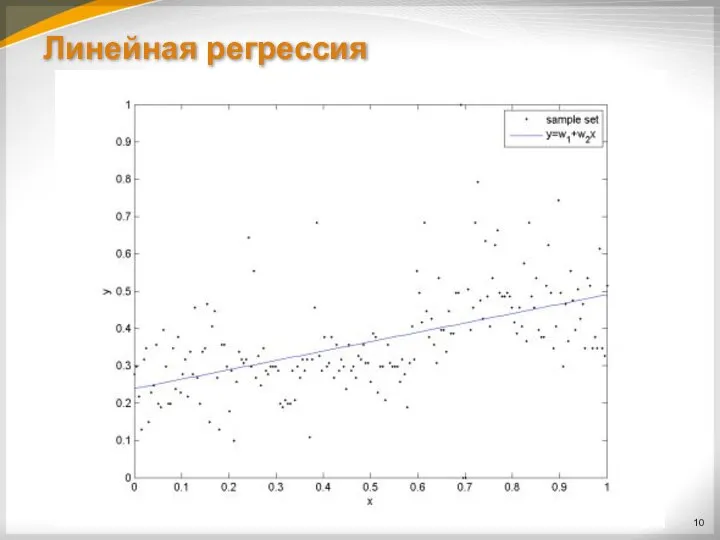
Линейная регрессия
Линейная регрессия — регрессионная модель, где зависимость критериальной переменной от регрессоров носит линейный характер:
Y = b0 + b1X1 + b2X2 + … + bMXM
b0…bM — коэффициенты (параметры) регрессии.

Линейная регрессия

Линейная регрессия

Регрессионный анализ

Нелинейная регрессия
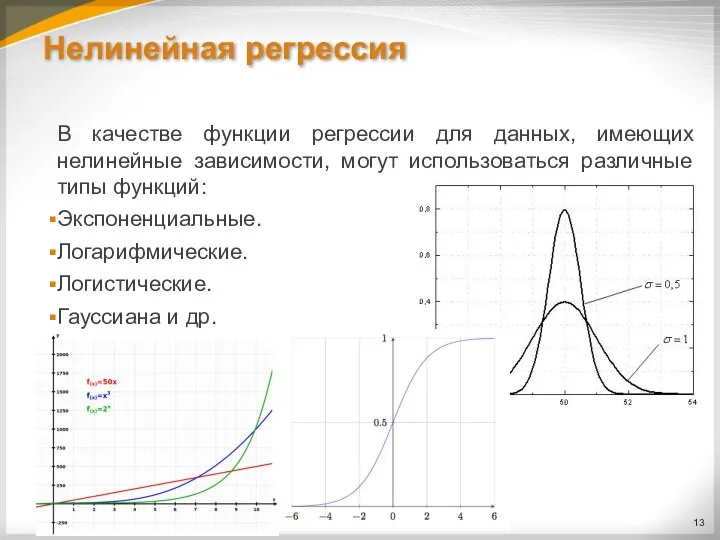
В качестве функции регрессии для данных, имеющих нелинейные зависимости, могут использоваться различные типы функций:
Экспоненциальные.
Логарифмические.
Логистические.
Гауссиана и др.

Регрессия и нейрон
Функция одного биологического нейрона может быть описана при помощи регрессии:
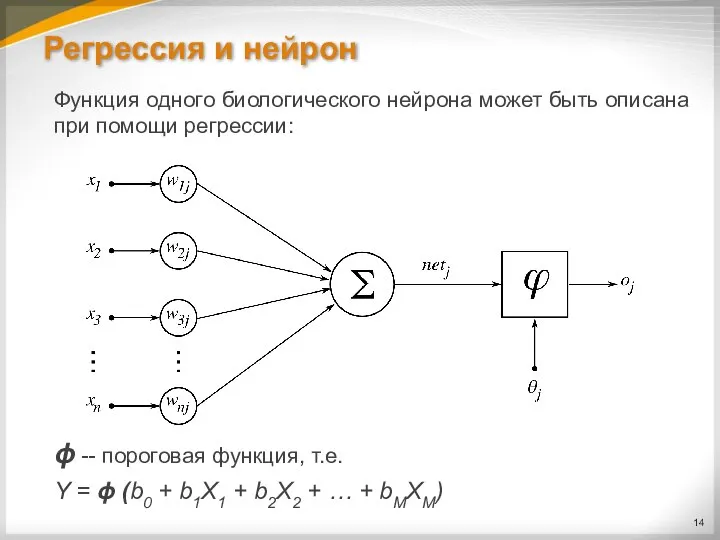
ϕ -- пороговая функция, т.е.
Y = ϕ (b0 + b1X1 + b2X2 + … + bMXM)

Регрессия и нейрон
Круг задач, которые можно решать при помощи регрессионного анализа, ограничен:
Одна зависимая (выходная) переменная.
Все переменные числено выражаемы.
Вид зависимости — известен.
Объединение нескольких моделей нейронов в сеть позволяет решать задачи другого уровня сложности.

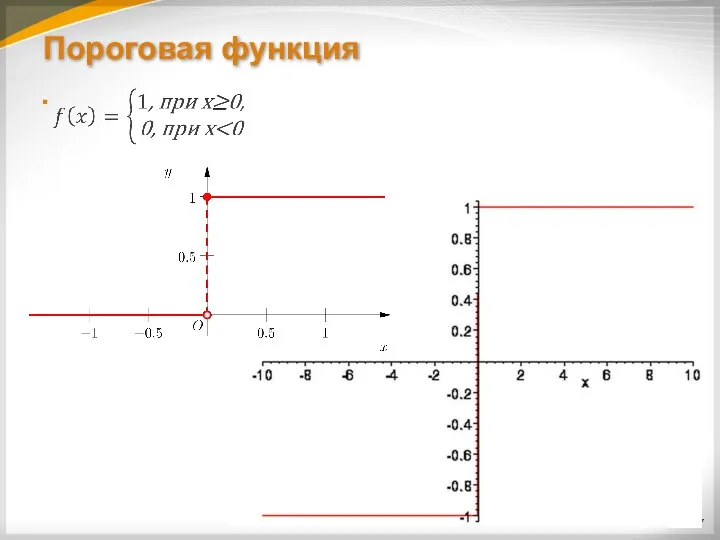
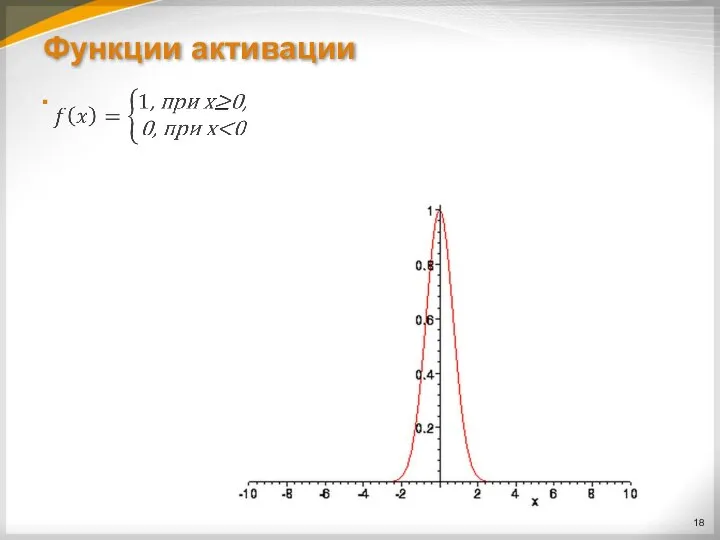
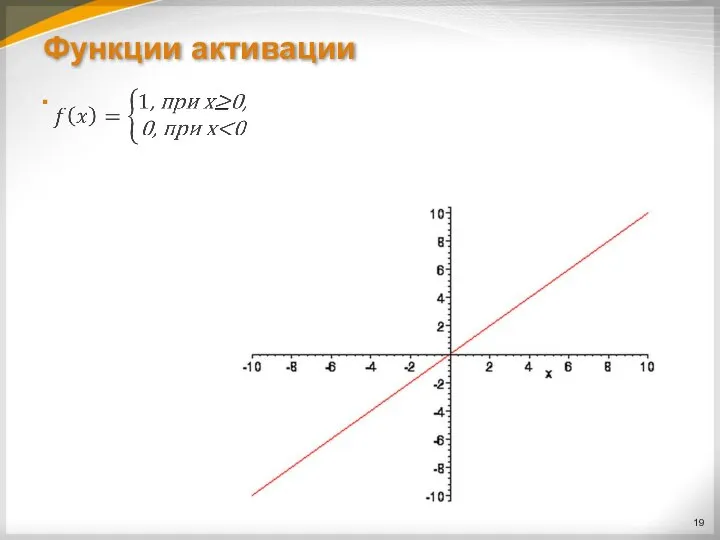
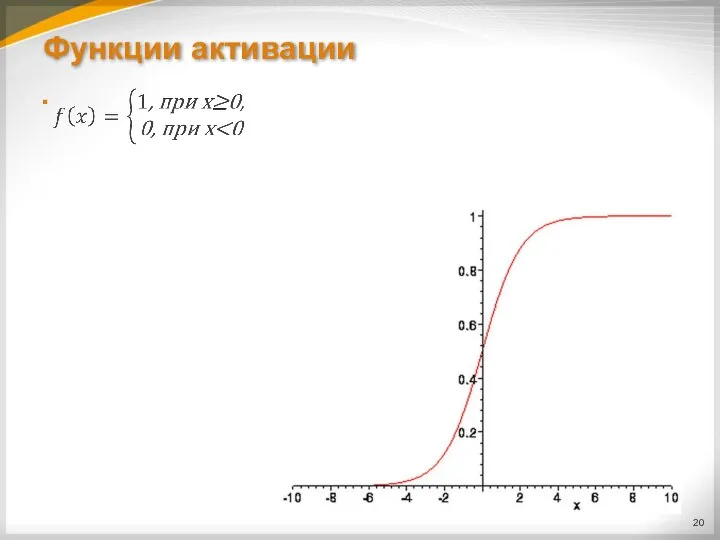
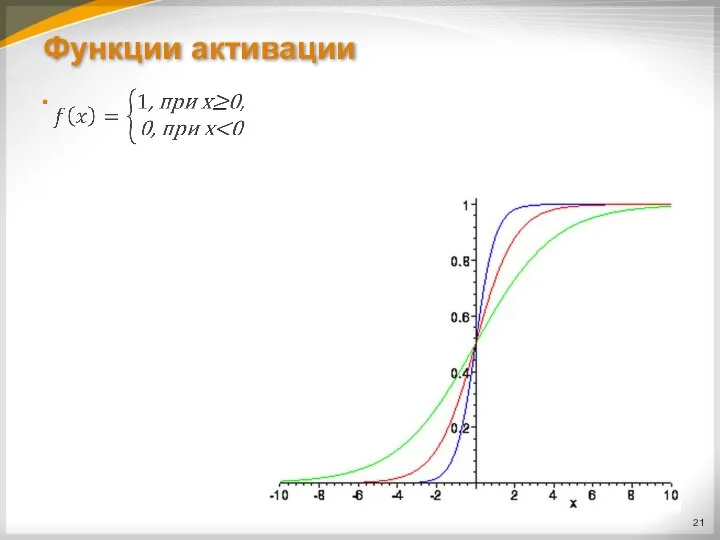
Функции активации
В искусственных нейронных сетях в качестве функций активации (функций, применяемых к сумме сигналов со входов), могут применяться различные типы функций.
Наиболее часто используется пороговая (ступенчатая) функция:

Пороговая функция

Функции активации

Функции активации

Функции активации

Функции активации

Сеть нейронов
Для функционирования нейронных сетей необходимо, чтобы сигнал передавался по сети из нейронов:

Сеть нейронов
Какую сеть можно сделать из искусственных нейронов?
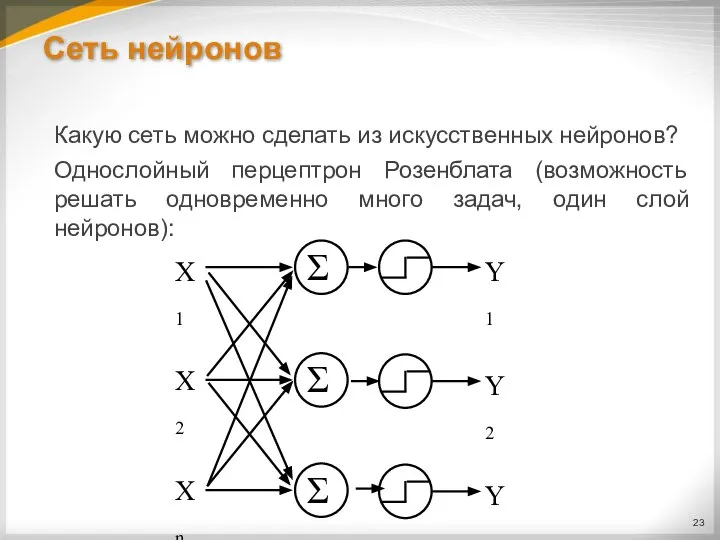
Однослойный перцептрон Розенблата (возможность решать одновременно много задач, один слой нейронов):

Сеть нейронов
Двухслойный перцептрон – расширение функциональности:
Скрытый слой Выходной слой

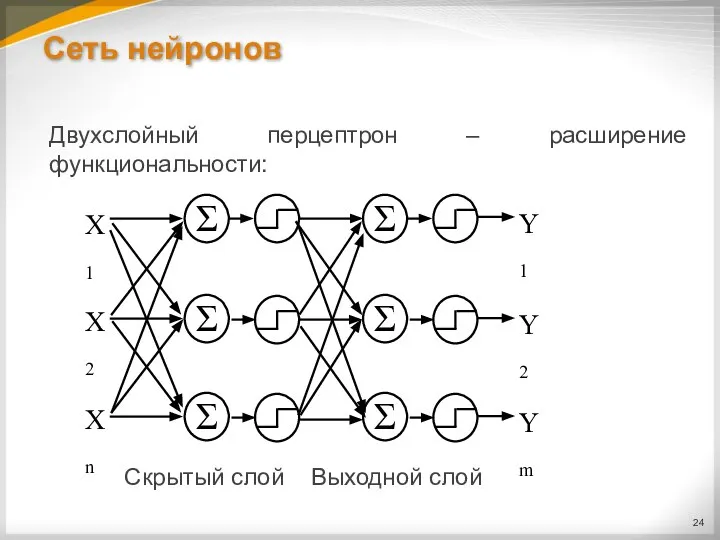
Сеть нейронов
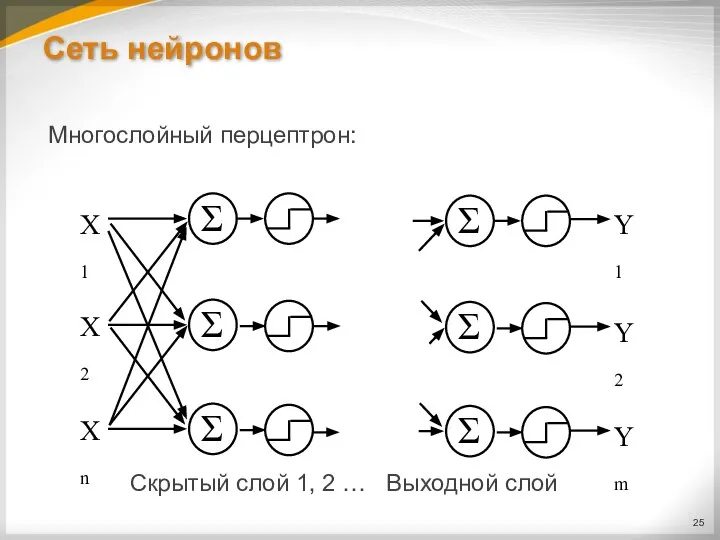
Многослойный перцептрон:
Скрытый слой 1, 2 … Выходной слой

Сеть нейронов
Практика

Сеть нейронов
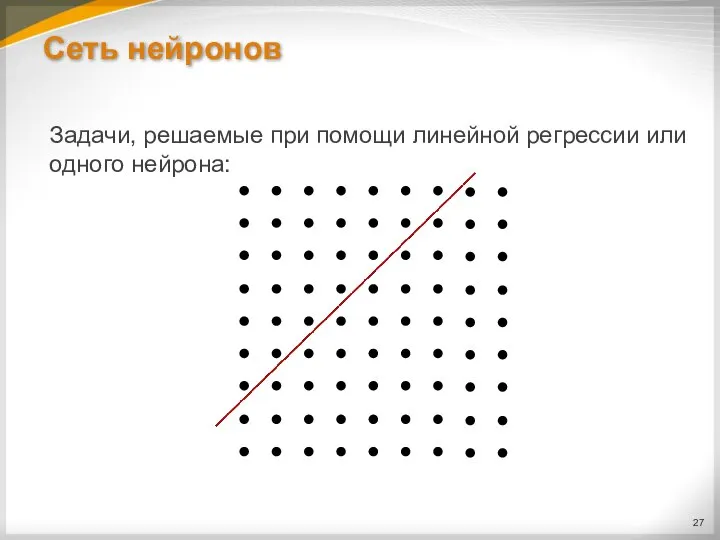
Задачи, решаемые при помощи линейной регрессии или одного нейрона:

Сеть нейронов
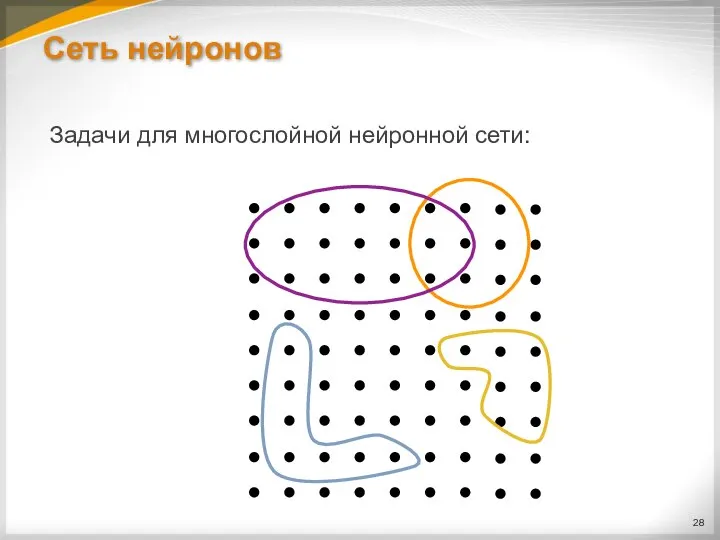
Задачи для многослойной нейронной сети:

Архитектура ИНС
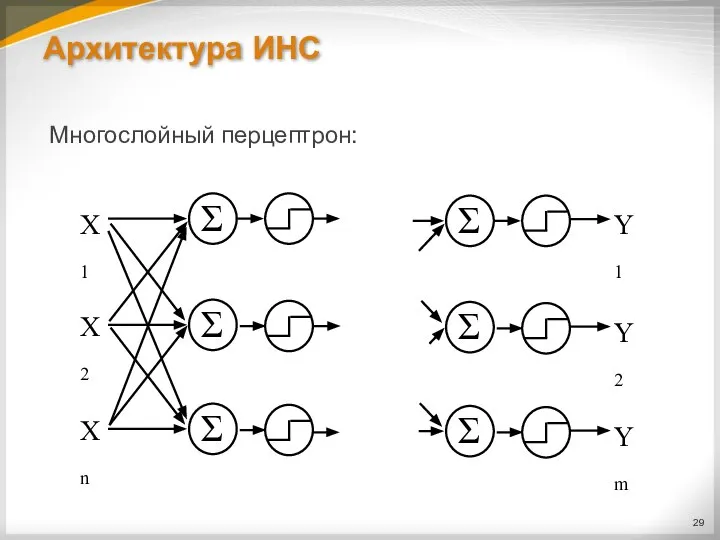
Многослойный перцептрон:

Архитектура ИНС
Круг задач, решаемых многослойным перцептроном:
Классификация (кластеризация).
Нелинейное, сложная регрессия.

Архитектура ИНС
Рекурсивные ИНС:

Архитектура ИНС
Рекурсивные ИНС:

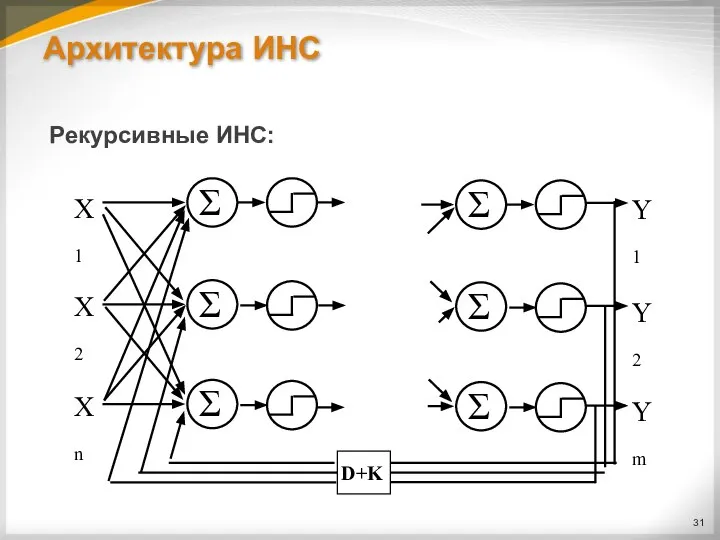
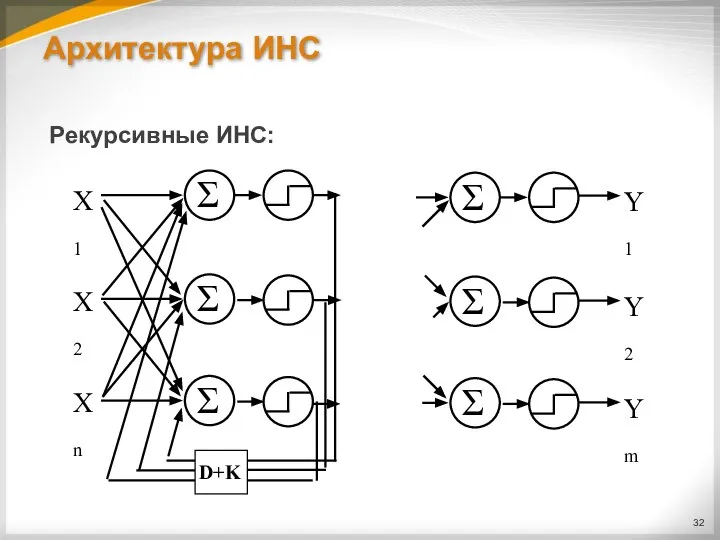
Архитектура ИНС
В рекурсивных многослойных ИНС используются данные от скрытого или выходного слоя, которые задерживаются, умножаются на некоторый коэффициент (обычно <1) и подаются на вход ИНС.
Рекурсивные многослойные нейронные сети используются для решения задач:
Обработки звука и речи.
Обработки сигналов.
Там, где важно учитывать предыдущее состояние системы.

Архитектура ИНС
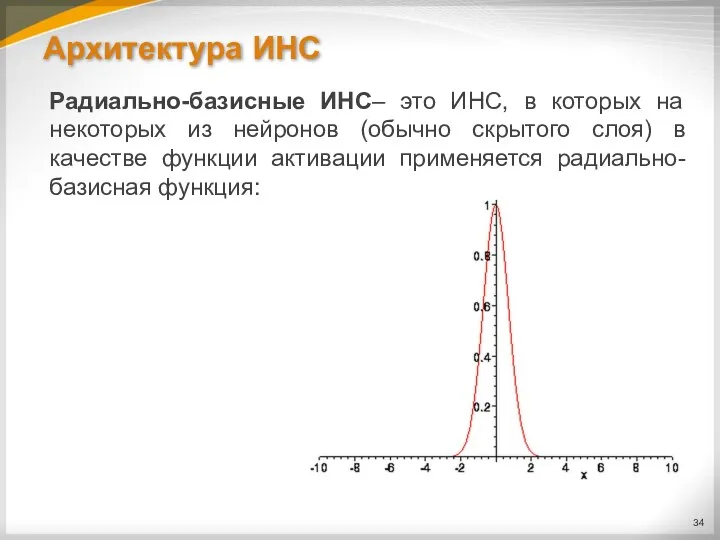
Радиально-базисные ИНС– это ИНС, в которых на некоторых из нейронов (обычно скрытого слоя) в качестве функции активации применяется радиально-базисная функция:

Архитектура ИНС
Радиально-базисные ИНС используются для анализа и прогнозирования различных сигналов (временных рядов), а также в теории управления.

Архитектура ИНС
Сверточные искусственные нейронные сети часто применяются для анализа изображений.

Состав ИНС
Количество тех или иных элементов ИНС зависит от решаемой задачи:
Входы ИНС:
число входов — по числу входных параметров;
тип входов (бинарные/рациональные числа) — по типу входных параметров.
Промежуточные (скрытые) слои:
число слоев — обычно один, в некоторых специальных случаях используется большее число слоев (например, чтобы уменьшить общее число нейронов);

Состав ИНС
Промежуточные (скрытые) слои:
число нейронов в слое — зависит требуемой способности сети к обобщению:
↑ число связей — ↑ способность к обобщению;
тип передаточной функции нейрона — исходя из специфики решаемой задачи, обычно ступенчатая, логистическая;
Выходной слой:
число нейронов — по числу требуемых ответов (или по числу вариантов выбора);
тип выходов — по типу требуемых ответов.