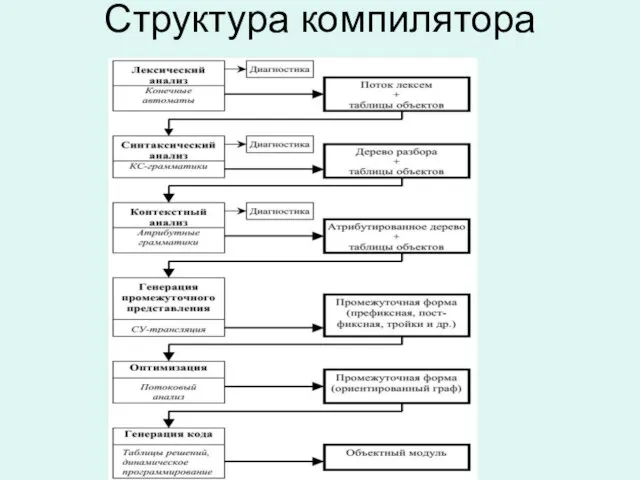
Слайд 5Модели алгоритмических преобразований

Слайд 14В регулярных выражениях опускают лишние скобки с
учётом того, что наивысшее предпочтение

(priority) имеет
операция итерации (повторения), затем идёт конкатенация,
и лишь затем - объединение.
Сокращение p+ для обозначения pp* (т.е. все итерации
кроме пустой цепочки).
Примеры регулярных выражений и обозначаемых ими
регулярных множеств:
а) a(e+a)+b – обозначает множество {a, b, aa};
б) a(a+b)* – обозначает множество всевозможных
цепочек, состоящих из a и b, начинающихся с a, например,
a(a+b)^3=a(a+b)(a+b)(a+b)=aaaa или abbb или abba…;
в)(a+b)*(a+b)(a+b)*–обозначает множество всех непустых цепочек, состоящих из a и b, то есть множество {a, b}+;
г) ((0+1)(0+1)(0+1))* – обозначает множество всех цепочек,
состоящих из нулей и единиц, длины которых делятся на 3.
Слайд 15Примеры и задачи на усвоение
Совпадают ли множества, соответствующие
двум данным РВ:
а) a*b и b

+ aa*b;
б) b(b+ab)*a и b(b*ab)*b*a;
в) b(ab+b)* и bb*a(bb*a)*.
Возьмём п. а) и посмотрим, какие множества
соответствуют первому и второму РВ соответственно:
a*b ={ b , ab , aab , …, anb , …}
b + aa*b ={ b , ab , aab , …, anb , …},
т.е. имеем с помощью РВ разные записи одного и
того же РМ.
Слайд 19Читающие (распознающие) автоматы

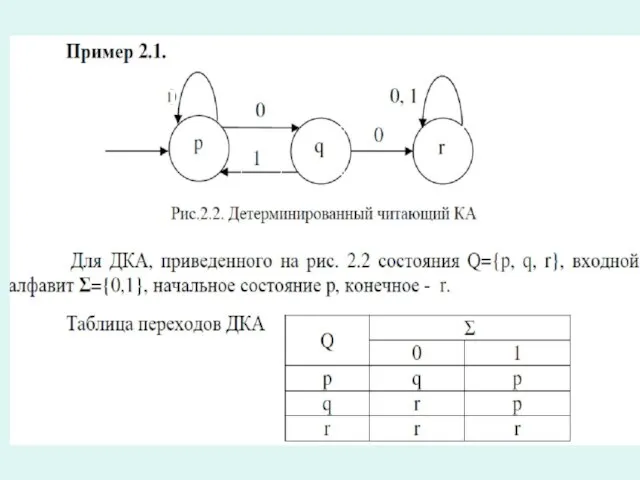
Слайд 23ДКА и НДКА
Различают детерминированные (ДКА) и недетерминированные (НДКА) конечные автоматы.
КА называется недетерминированным
(НДКА),

если в диаграмме его состояний из одной вершины исходит несколько дуг с одинаковыми символами. Если таких вершин нет, то это ДКА.
Слайд 26Теорема Клини. Две задачи КА
Теорема Клини содержит два утверждения:
1. Каждое регулярное

выражение определяет регулярный язык
2. Каждый регулярный язык может быть задан некоторым R- выражением.
Задача синтеза состоит в построении конечного автомата, распознающего язык, заданный некоторым регулярным выражением.
Задача анализа состоит в том, чтобы по диаграмме конечного автомата К записать R-выражение, для которого соответствующий ему R-язык совпадает с
языком, распознаваемым автоматом К.
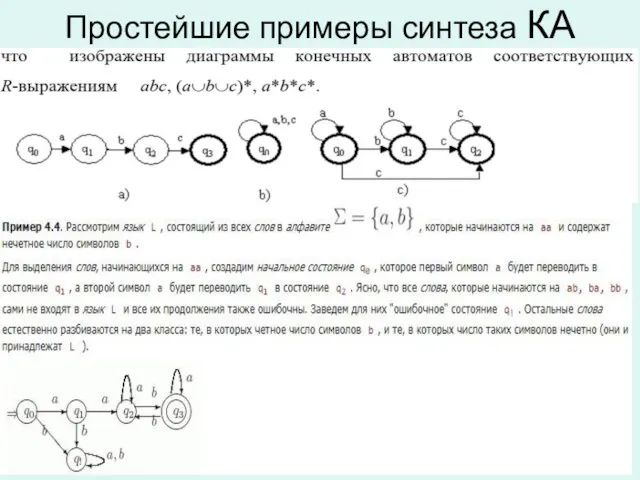
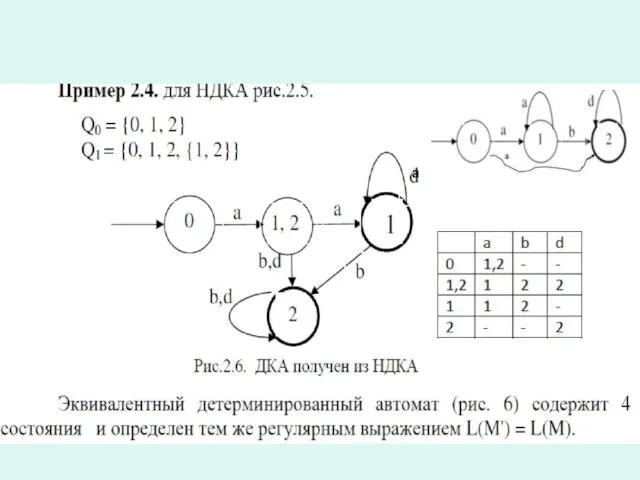
Слайд 28Преобразование регулярного выражения в КА

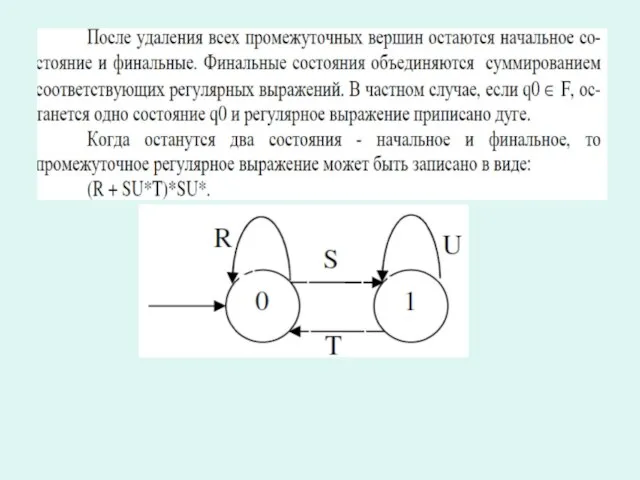
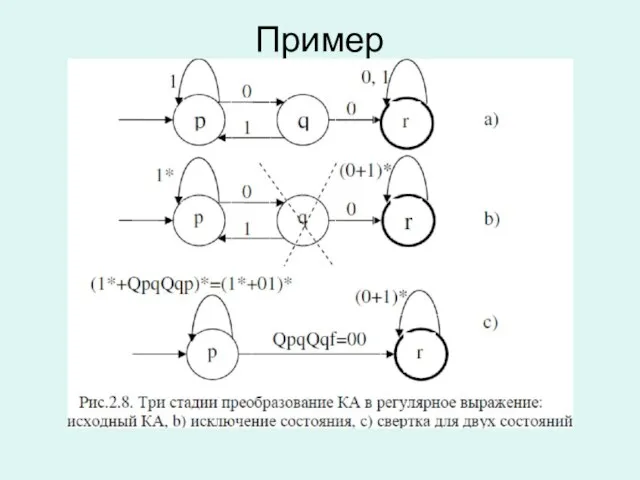
Слайд 35Преобразование КА в регулярное выражение

Слайд 39Обратное преобразование в НДКА
Преобразование в ДКА
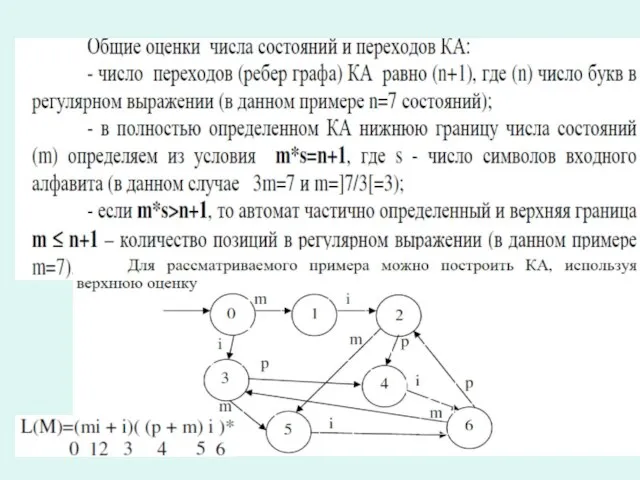
L(M)=(1*+01)*00(0+1)*
0 0 10 23
Q0

= {q0, q1, q2, q3}
Q1 = {q0, q1, q2, q3,{q1, 2}}.
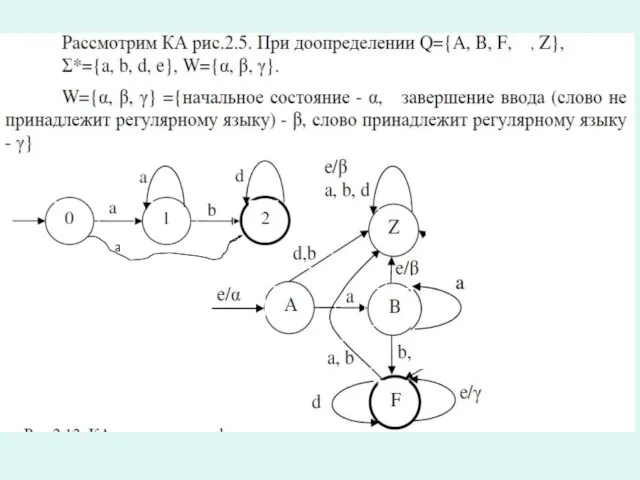
Состояния q1 и q2 не достижимы из начального состояния q0 и могут быть исключены. Получим исходный КА рис.2.2. с состояниями
Q1= {q0, q3,{q1, 2}}

































 Коммуникационное VS Информационное общество
Коммуникационное VS Информационное общество Кодирование информации
Кодирование информации КТ2
КТ2 Алгоритмизация и программирование
Алгоритмизация и программирование Межрегиональная Общественная организация Центр противодействия кибер преступлениям Я выбираю жизнь
Межрегиональная Общественная организация Центр противодействия кибер преступлениям Я выбираю жизнь Компьютерная графика
Компьютерная графика HTML – язык разметки гипертекста
HTML – язык разметки гипертекста Криптография
Криптография Per aspera ad astra (РААА)
Per aspera ad astra (РААА) Анализ экспериментальных данных: компьютерный лабораторный практикум
Анализ экспериментальных данных: компьютерный лабораторный практикум Компьютерные сети
Компьютерные сети Предмет, методы и система информационного права
Предмет, методы и система информационного права Логобук. Что включает в себя логобук?
Логобук. Что включает в себя логобук? slides9-1
slides9-1 Компьютер-исполнитель команд. Программный принцип работы компьютера
Компьютер-исполнитель команд. Программный принцип работы компьютера Повреждения книжных изданий
Повреждения книжных изданий Отношения между объектами
Отношения между объектами Особенности материалов для соцсетей: пост, лонгрид подкаст
Особенности материалов для соцсетей: пост, лонгрид подкаст Сеть провайдеров ШЕНГЕН
Сеть провайдеров ШЕНГЕН Операционная система Windows
Операционная система Windows Социальные сети на 01.08.18
Социальные сети на 01.08.18 Пиксельные задачи первого типа
Пиксельные задачи первого типа Компьютерные вирусы и антивирусные программы
Компьютерные вирусы и антивирусные программы Информационные технологии в психологии. Анализ Интернет-ресурсов
Информационные технологии в психологии. Анализ Интернет-ресурсов Практикум: Составление блок-схем алгоритмов линейной структуры
Практикум: Составление блок-схем алгоритмов линейной структуры Лекции по информатике (часть 1)
Лекции по информатике (часть 1) Вводный урок. Вспомнить всё!
Вводный урок. Вспомнить всё! Информационно-коммуникационные технологии обучения (ИКТ)
Информационно-коммуникационные технологии обучения (ИКТ)