Двоичное кодирование данных

Цель кодирования: представление текста, графики, звука, любых других данных в виде двоичного (машинного) кода
Машинный код состоит из последовательности битов.
1 бит принимает значения

Чтобы обрабатывать данные, надо их обозначить. Дать имя каждому объекту, подлежащему обработке
Но из одного бита можно получить только два имени!
Для задания имен объектов требуется
объединять биты в группу

Двумя битами уже можно обозначить 4 объекта:
Из трех бит получается
8 вариантов (8 независимых кодов):
000 001 010 100
011 101 110 111
Получить 4 независимых кода

Формула определения числа независимых кодов в двоичной системе счисления:
K = 2N
K – число получаемых
независимых кодов
N – число бит в группе

С начала 70-х годов XX века в абсолютном большинстве компьютеров биты группируются в едином стандарте, который называется байт
1 байт = 8 бит
}
Из одного байта можно получить 28 = 256 независимых кодов

Биты объединяются в байты для того же, для чего буквы объединяются в слова: чтобы иметь возможность именовать объекты и процессы обработки информации.
Объединение в байты настолько важно, что характеристики компьютера, размер файлов и пр. измеряется не в битах, а в байтах.

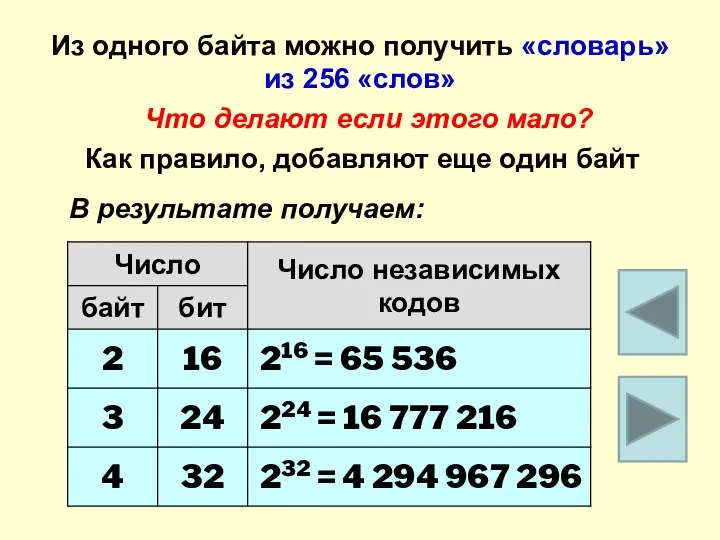
Из одного байта можно получить «словарь» из 256 «слов»
Что делают если этого мало?
Как правило, добавляют еще один байт
В результате получаем:

Пример однобайтной кодировки
(256 кодов):
Кодировка текста ASCII

Распределение кодов:
0 – 31 → аппаратные коды, с клавиатуры не вводятся;
32 – 127 → символы английской клавиатуры;
128 – 255 → национальные системы кодировки;

Для кириллицы самая распространенная (но не единственная) кодировка – это Windows 1251
Пример соответствия символов кодам:

Пример двухбайтной кодировки
(216 = 65 536 кодов):
Кодировка текста UNICODE

В массив из 65,5 тысяч единиц вмещаются все современные национальные алфавиты плюс много служебных знаков
Преимущество UNICODE: это единый стандарт для всех символов текста

Пример трехбайтной кодировки (224 = = 16 777 216 кодов): цветовая модель RGB
Red, Green, Blue →
Красный, Зеленый, Синий
Цвет пикселя, линии, заливки задается тремя компонентами, каждый из которых имеет 256 уровней яркости

Цвета RGB обычно записывают в виде:
XXYYZZ
где XX, YY, ZZ – шестнадцатирич-ные коды красного, синего, зеленого цветов
Коды принимают целые значения от 0 (00) до 255 (FF)

Всего с помощью RGB можно создать ≈ 16,8 миллионов цветовых оттенков.
Человек столько различить не может. Но таковы правила записи данных в компьютер
Модель RGB используется при описании цвета в большинстве аппаратных устройств: мониторе, сканере, цифровой фото и видео аппаратуре, графическом планшете и др.
Человеческий глаз работает в модели RGB, что первично
Однако в RGB нельзя создать многие спектрально чистые цвета, которые способен видеть человек

Здесь «а» принимает значения от 0 до 255. Обычно пишется в десятичной форме:
Пример четырехбайтной кодировки (232 = 4 294 967 296 кодов):
IP-адресация в Интернете
IP-адрес: а1.а2.а3.а4
Таким образом, в Интернете не может одновременно находиться более ≈ 4 миллиардов 300 миллионов компьютеров – на большее не хватит адресов
192.168.0.12