Слайд 2Целью настоящей работы является визуализация в графическом редакторе Blender топологической операции склейки

двумерных многообразий на примере сферы.
Объектом исследования являются двумерные дифференцируемые многообразия и их топологические инварианты.
Слайд 3Основные определения и факты

Слайд 4Ввести понятие ручки и ленты Мебиуса!!! Дополнить рисунками

Слайд 6Математическое обоснование возможности выполнения операции склейки в графических редакторах
В данном разделе рассмотрим

операцию “приклеивания” ручки к сфере. С точки зрения дальнейшей визуализации этой процедуры в графическом 3d редакторе остановимся на двух вариантах такой склейки.
Слайд 9 Blender
Среди уникальных особенностей Blender следует отметить следующие.
1. Кроссплатформенность. Blender одинаково хорошо

и стабильно работает в Linux, Windows и др. операционных системах.
2. Размер. По сравнению с коммерческими разработками размер этого редактора совершенно мизерный --- всего несколько десятков мегабайт.
3. Системные требования. Программа может полноценно функционировать даже на ПК с очень слабыми конфигурациями, вплоть до нетбуков. Минимальные требования к системе более чем скромные: процессор с одним ядром, работающий на частоте 1 ГГц, оперативная память 512 Мбайт и видеокарта с поддержкой Open GL и объемом памяти не ниже 64 Мбайт.
Слайд 10 Визуализация топологических операций в Blender
Операция склейки
Далее будут показаны
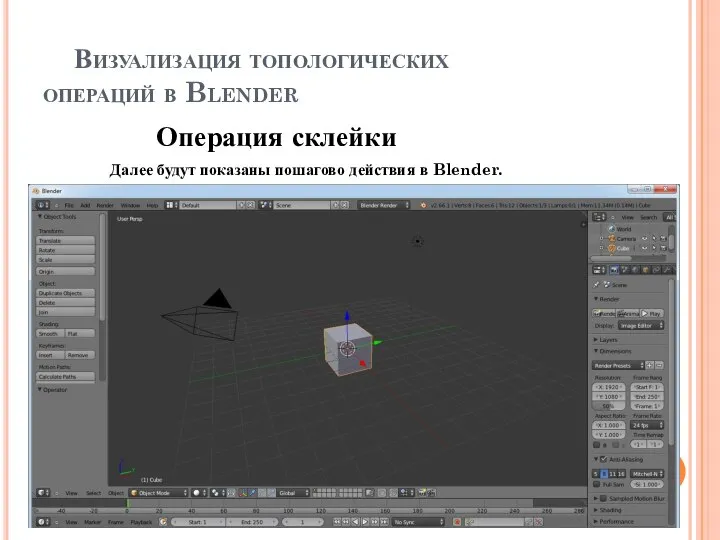
пошагово действия в Blender.
Слайд 11Удаляем стандартный куб, добавляем меш окружность
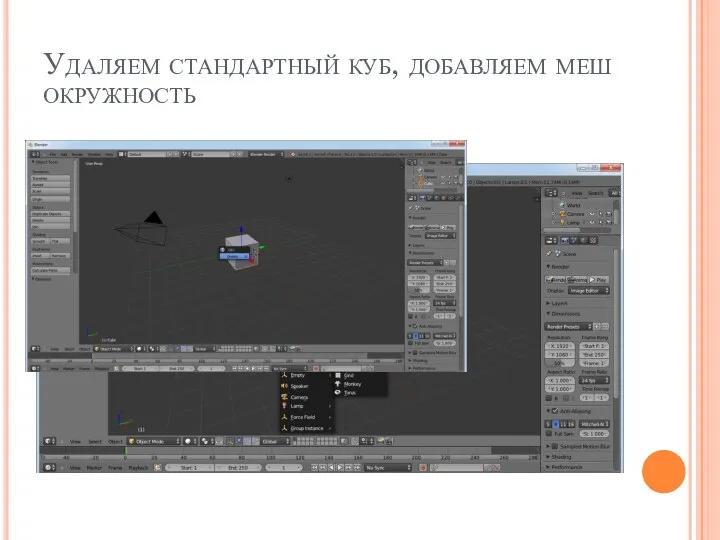
Слайд 12Уменьшаем диаметр окружности, поворачиваем окружность по оси Ох на 90 градусов
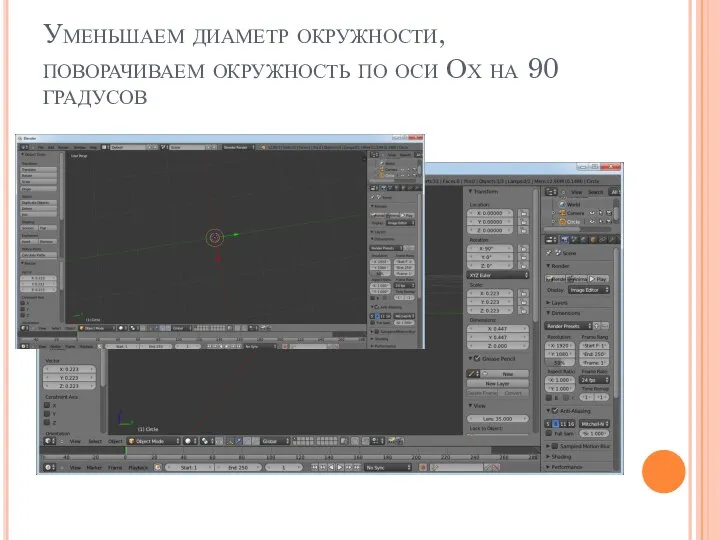
Слайд 13Используем модификатор screw, В результате получаем новый меш, гомеоморфный тору.
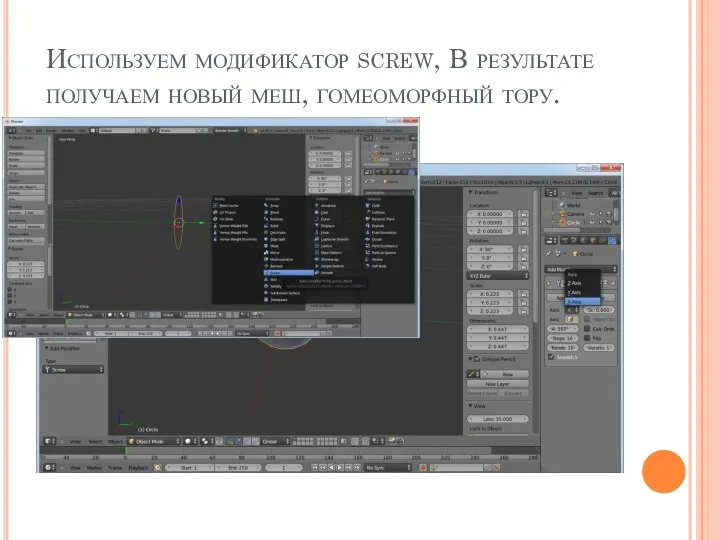
Слайд 14Перемешаем 3d курсор, растягиваем меш до ширины, 3d курсора.
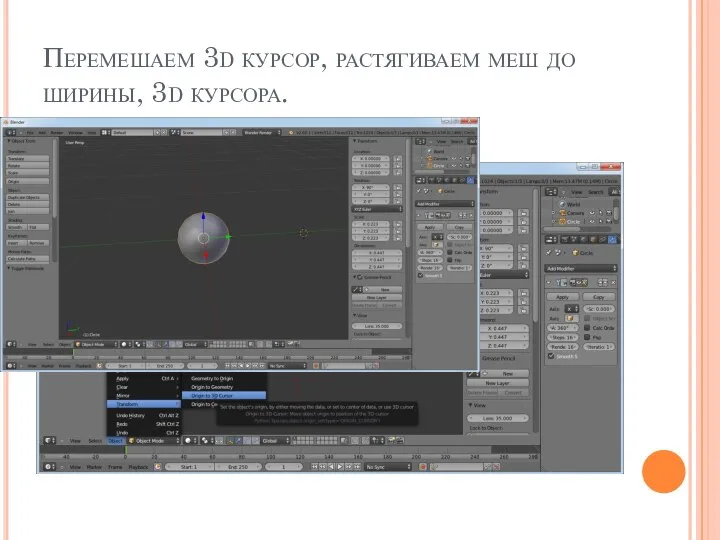
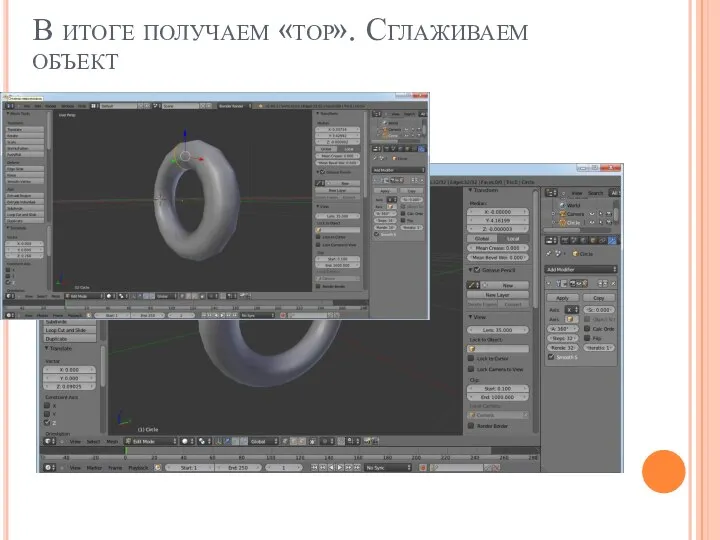
Слайд 15В итоге получаем «тор». Сглаживаем объект
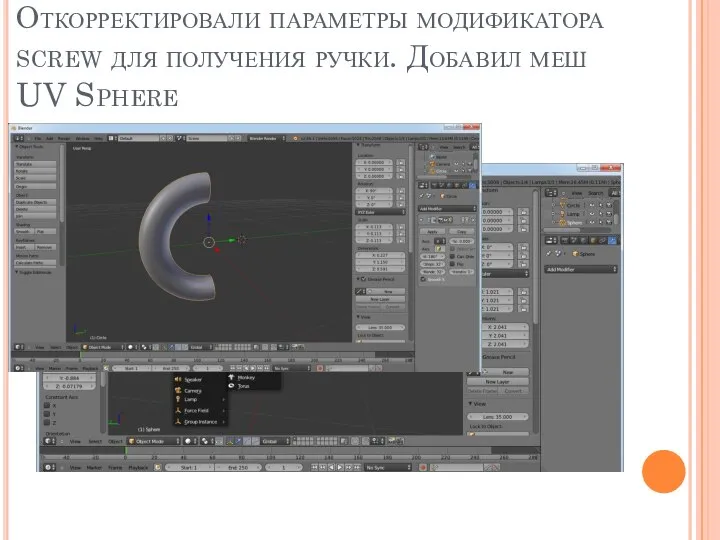
Слайд 16Откорректировали параметры модификатора screw для получения ручки. Добавил меш UV Sphere
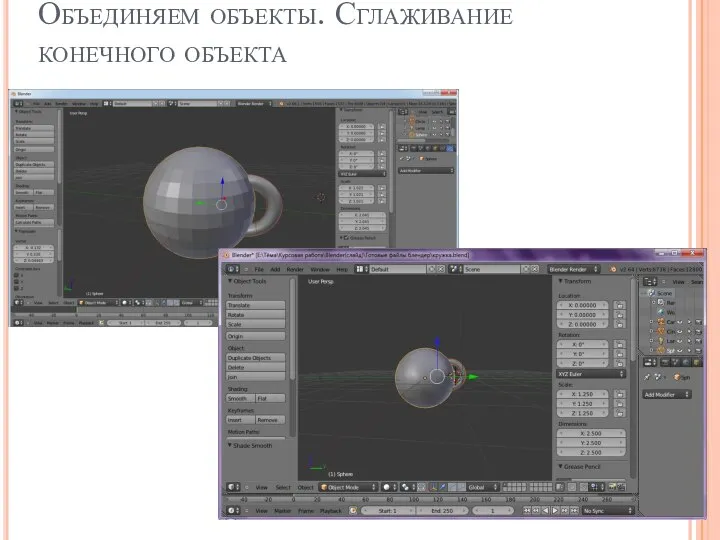
Слайд 17Объединяем объекты. Сглаживание конечного объекта
















 Оператор множественного выбора САSE
Оператор множественного выбора САSE Информация вокруг нас
Информация вокруг нас Вредоносное программное обеспечение и методы борьбы с ним
Вредоносное программное обеспечение и методы борьбы с ним 7-1-6 (1)
7-1-6 (1) Урок по информатике. Работа с Microsoft Word
Урок по информатике. Работа с Microsoft Word Визуальное программирование. Среда программирования Scratch 3.17.2
Визуальное программирование. Среда программирования Scratch 3.17.2 Операторы организации циклов. Простой и составной операторы. Лекция 6
Операторы организации циклов. Простой и составной операторы. Лекция 6 Аналитика упоминаний о коммерческих проектах Euromed Group во внешних источниках за Q2 2021. Angry Analytics
Аналитика упоминаний о коммерческих проектах Euromed Group во внешних источниках за Q2 2021. Angry Analytics Реклама в современном мире
Реклама в современном мире Презентация на тему Алгебра логики Логическое умножение, сложение и отрицание
Презентация на тему Алгебра логики Логическое умножение, сложение и отрицание  Электронные ресурсы МОБ Екатеринбурга
Электронные ресурсы МОБ Екатеринбурга тиворкс
тиворкс Data science. Кластеризация
Data science. Кластеризация Теоретические основы компьютерной безопасности. Лекция №10. Критерии и защищенности компьютерных систем классы
Теоретические основы компьютерной безопасности. Лекция №10. Критерии и защищенности компьютерных систем классы Презентация на тему Мобильная связь (поколение мобильных телефонов)
Презентация на тему Мобильная связь (поколение мобильных телефонов)  Продвижение в instagram
Продвижение в instagram Технологии информационного менеджмента в системах социальной защиты
Технологии информационного менеджмента в системах социальной защиты Компания Denux. Система для поиск вакансии
Компания Denux. Система для поиск вакансии Физические основы компьютерной графики. Зрение, спектр, цвет, свет, цветовые модели. Лекция №2
Физические основы компьютерной графики. Зрение, спектр, цвет, свет, цветовые модели. Лекция №2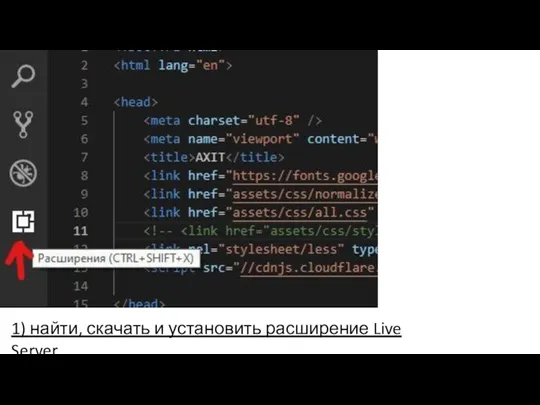 Расширение Live Server
Расширение Live Server Аппаратура цифровых радиорелейных линий МИК-РЛ
Аппаратура цифровых радиорелейных линий МИК-РЛ Безопасность в Интернете
Безопасность в Интернете Табличные информационные модели
Табличные информационные модели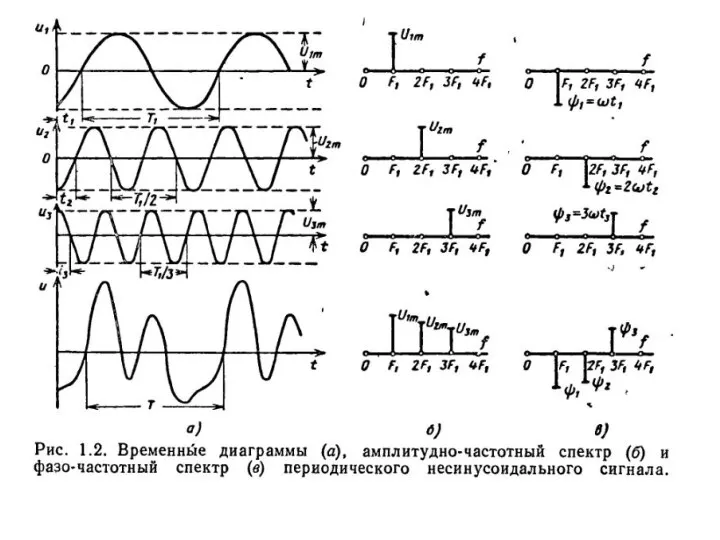 Теорема Котельникова
Теорема Котельникова Алгоритмы обработки массивов
Алгоритмы обработки массивов Разработка программных модулей программного обеспечения для компьютерных систем
Разработка программных модулей программного обеспечения для компьютерных систем Знакомим родителей с программой ПиктоМир
Знакомим родителей с программой ПиктоМир Настройка интернета
Настройка интернета