Содержание
- 2. Некоторое сообщение содержит только буквы А, Б, В, Г, Д, причём известно их количество: А —
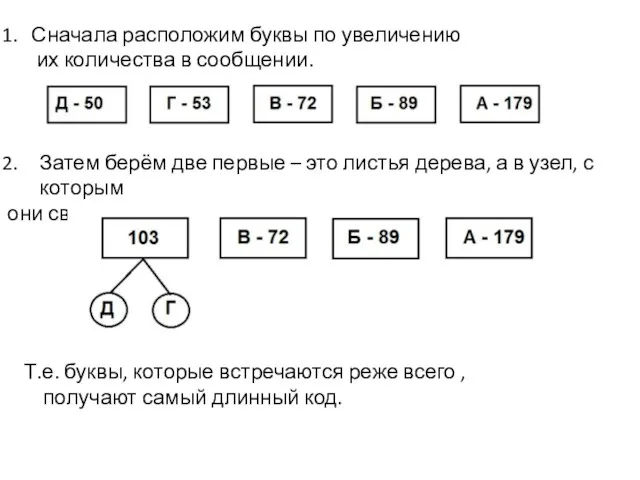
- 3. Сначала расположим буквы по увеличению их количества в сообщении. Затем берём две первые – это листья
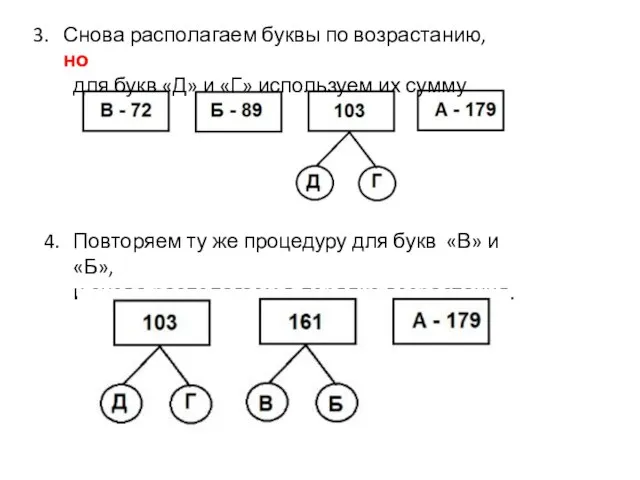
- 4. Снова располагаем буквы по возрастанию, но для букв «Д» и «Г» используем их сумму Повторяем ту
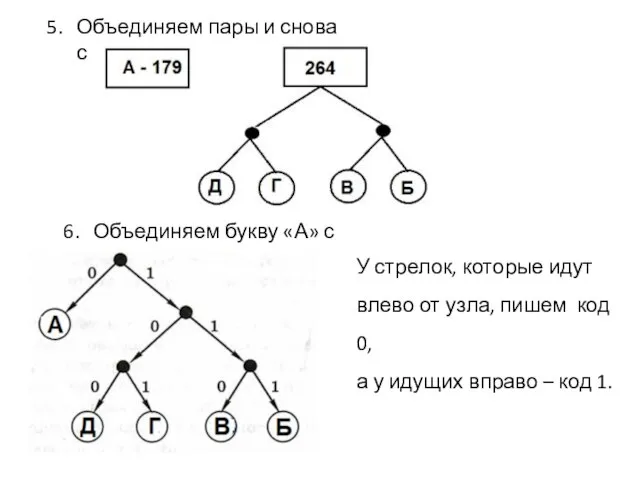
- 5. Объединяем пары и снова сортируем. Объединяем букву «А» с деревом. У стрелок, которые идут влево от
- 6. Считаем сумму: 1*179 + 3*264 = 179+792 = 971 ОТВЕТ: 971
- 7. Некоторое сообщение содержит только буквы Ю, В, Е, Л, И, Р, известно их количество: Ю—9, В—15,
- 9. Скачать презентацию



 Стратегия рекламного продвижения
Стратегия рекламного продвижения Разработка макета WEB сайта на заданную тему
Разработка макета WEB сайта на заданную тему Прикладное программное обеспечение для анализа рынка на основе данных социальных сетей
Прикладное программное обеспечение для анализа рынка на основе данных социальных сетей Объекты окружающего мира
Объекты окружающего мира Знакомство с Microsoft Word. Урок 1
Знакомство с Microsoft Word. Урок 1 Data Warehouse Concepts and Architectures
Data Warehouse Concepts and Architectures Некрос вышел из-под контроля
Некрос вышел из-под контроля Режимы и способы обработки данных
Режимы и способы обработки данных Фітнес-асистент
Фітнес-асистент Методологии разработки ПО
Методологии разработки ПО Презентация на тему Что то у них с памятью стало...
Презентация на тему Что то у них с памятью стало... 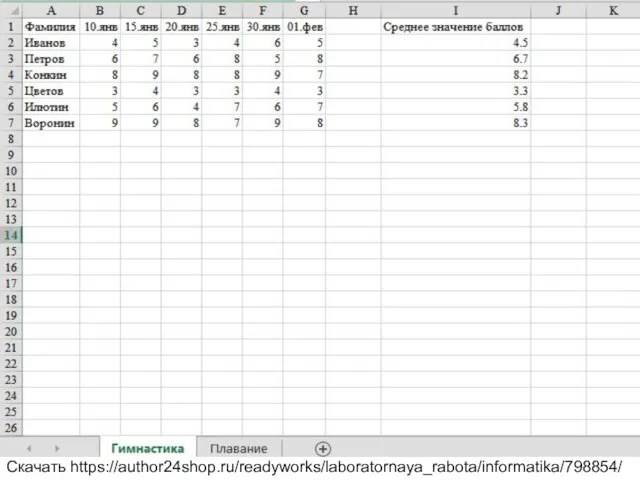 Связь между листами. Лабораторная работа
Связь между листами. Лабораторная работа Обработка ошибок
Обработка ошибок Итерационные алгоритмы и программы. Лекция 7
Итерационные алгоритмы и программы. Лекция 7 Миссионерская церковь копимизма
Миссионерская церковь копимизма Программирование циклических алгоритмов. Начала программирования
Программирование циклических алгоритмов. Начала программирования Шаблон для составления скрипта
Шаблон для составления скрипта Работа в слоях. Коллажи
Работа в слоях. Коллажи Презентация на тему GPS - навигаторы
Презентация на тему GPS - навигаторы  Для конкурса Интернешка
Для конкурса Интернешка Послуги наступного покоління NGS
Послуги наступного покоління NGS Конструкторы интерактивных заданий
Конструкторы интерактивных заданий Законы алгебры логики
Законы алгебры логики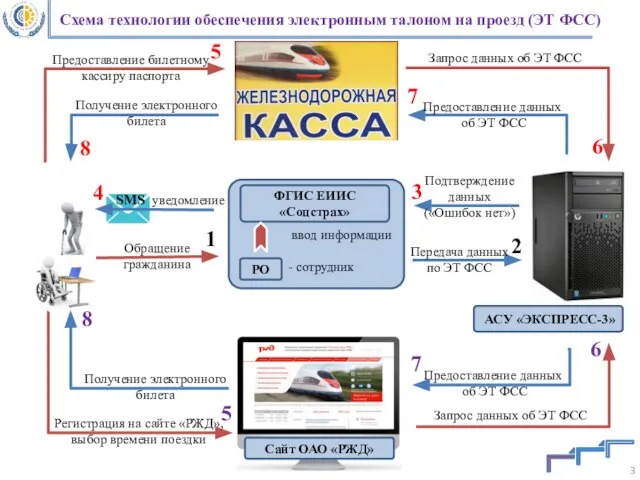 Схема технологии обеспечения электронным талоном на проезд (ЭТ ФСС)
Схема технологии обеспечения электронным талоном на проезд (ЭТ ФСС) Prezentatsia_Microsoft_PowerPoint_1
Prezentatsia_Microsoft_PowerPoint_1 Внутренняя память компьютера
Внутренняя память компьютера Курсовое проектирование. Темы для ознакомления
Курсовое проектирование. Темы для ознакомления Циклы. Повторение
Циклы. Повторение