Содержание
- 2. Что нужно знать: принципы кодирования чисел в позиционных системах счисления чтобы перевести число, скажем, 12345N, из
- 3. число 10N-1 записывается как N девяток: число 10N-10M = 10M · (10N-M – 1) записывается как
- 4. поскольку , получаем , откуда следует, что число 3N записывается в троичной системе как единица и
- 5. можно сделать аналогичные выводы для любой системы счисления с основанием a: число aN в системе счисления
- 6. Пример 1 Значение арифметического выражения: 99 – 39 + 919 – 19 записали в системе счисления
- 7. Пример 1 Сначала рассмотрим часть выражения, в которой имеется два расположенных подряд «минуса»: 318 - 39
- 8. Пример 1 Прибавление значения 338 не изменит количества «двоек» в троичном числе: слева от имеющихся цифр
- 9. Пример 2 Значение арифметического выражения: 98 + 35 – 9 записали в системе счисления с основанием
- 10. Пример 2 Решение: приведём все слагаемые к виду 3N и расставим в порядке убывания степеней: 98
- 11. Пример 3 Сколько значащих нулей в двоичной записи числа 4512 + 8512 – 2128 – 250
- 12. Пример 3 старшая степень двойки – 21536, двоичная запись этого числа представляет собой единицу и 1536
- 13. Пример 3 используем теперь равенство , так что – 2128 = – 2129 + 2128; получаем
- 14. Пример 4 Сколько единиц в двоичной записи числа 42015 + 8405 – 2150 – 122 приведём
- 15. Пример 4 в нашем случае вы выражении 24030 + 21215 – 2150 – 27 + 22
- 16. Пример 5 Решите уравнение Ответ запишите в троичной системе счисления. Основание системы счисления указывать не нужно.
- 17. Пример 6 Сколько единиц в двоичной записи числа 42014 + 22015 – 8 Решение: приведём все
- 18. Пример 7 Решите уравнение . Ответ запишите в шестеричной системе счисления. Основание системы счисления указывать не
- 19. Пример 8 Запись десятичного числа в системах счисления с основаниями 3 и 5 в обоих случаях
- 20. Пример 9 Запись числа 6710 в системе счисления с основанием N оканчивается на 1 и содержит
- 21. Пример 9 выпишем кубы и четвертые степени первых натуральных чисел, которые являются делителями числа 66: видим,
- 22. Пример 10 Запись числа 38110 в системе счисления с основанием N оканчивается на 3 и содержит
- 23. Пример 10 с другой стороны, запись числа содержит 3 цифры, то есть неравенство дает (так как
- 24. Пример 11 Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 25, запись которых
- 26. Скачать презентацию























 Симулятор установки windows 5
Симулятор установки windows 5 Клавиатура
Клавиатура Модемы и факсмодемы
Модемы и факсмодемы Создание меню в ЛИСПе
Создание меню в ЛИСПе Форсайт. Регламентный отчет
Форсайт. Регламентный отчет Инструкция к обнулению ЗН и КЗ
Инструкция к обнулению ЗН и КЗ Современные математические подходы в моделировании
Современные математические подходы в моделировании Создание формы объектов
Создание формы объектов Оформление кредитов в NEW POS
Оформление кредитов в NEW POS Презентация на тему Правила техники безопасности и правила поведения в компьютерном классе
Презентация на тему Правила техники безопасности и правила поведения в компьютерном классе  Организация хранения информации в компьютере
Организация хранения информации в компьютере Программирование на языке Pascal
Программирование на языке Pascal Онлайн-конструктора документов Октима
Онлайн-конструктора документов Октима Ур. 26 Программирование линейных алгоритмов
Ур. 26 Программирование линейных алгоритмов Поиск информации с помощью браузера Internet Explorer
Поиск информации с помощью браузера Internet Explorer Этические и правовые нормы информационной деятельности людей. Виды программного обеспечения
Этические и правовые нормы информационной деятельности людей. Виды программного обеспечения Джойстик
Джойстик TA_lec2
TA_lec2 1240031 (2)
1240031 (2) Правки по стилистике сайта
Правки по стилистике сайта 30 сентября - профессиональный праздник всех пользователей и работников Интернет-индустрии. Международный День Интернета
30 сентября - профессиональный праздник всех пользователей и работников Интернет-индустрии. Международный День Интернета Этапы развития сервиса микроблоггинга Твиттер
Этапы развития сервиса микроблоггинга Твиттер Киберпреступники
Киберпреступники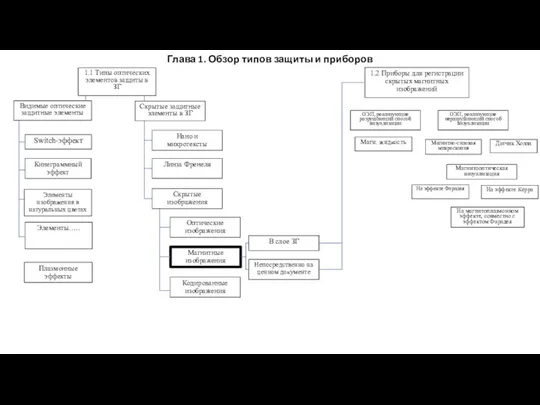 Обзор типов защиты и приборов
Обзор типов защиты и приборов Время приключений. Закрытое бета - тестирование
Время приключений. Закрытое бета - тестирование Библиографическая информация
Библиографическая информация Инструкция по выбытию 11 классов в НОБД и переводу школы на новый учебный год
Инструкция по выбытию 11 классов в НОБД и переводу школы на новый учебный год Подача заявления для участия в программе на портале Работа в России
Подача заявления для участия в программе на портале Работа в России